图像处理100题习题与代码（21~30）

题目原地址：https://github.com/gzr2017/ImageProcessing100Wen

我的github地址：https://github.com/LeonG7/image_100question

前言：

这是图像处理100题的题目记录以及我自己写的参考代码，感谢@gzr2017提供中文翻译。

所有代码由jupyter book软件导出，如需可执行源代码，请在我的github下载。

如有任何问题或错误，欢迎在评论区讨论和指正

---

图像处理21~30题

读取图片：

import cv2
import numpy as np
%matplotlib inline
from matplotlib import pyplot as plt

img = cv2.imread("imori.jpg")
img_gamma = cv2.imread("imori_gamma.jpg")
img_dark = cv2.imread("imori_dark.jpg")
img = img[:,:,[2,1,0]]
img_gamma = img_gamma[:,:,[2,1,0]]
img_dark = img_dark[:,:,[2,1,0]]

1.直方图归一化(Histogram Normalization)

又称灰度变换，主要适用于将灰度图片还原到彩色图片

公式如下：
$$x_{out}=\{\begin{array}{ll}a& (\text{if}{x}_{in}<c)\\ \frac{b-a}{d-c}(x_{in}-c)+a& (\text{else if}c\le x_{in}<d)\\ b& (\text{else})\end{array}$$

def normalHist(img):
    a = 0
    b = 255
    c = img.min()
    d = img.max()
    img = (b-a)/(d-c)*(img-c)+a
    img = img .astype(np.uint8)
    return img

imgshow = plt.imshow(img_dark)
plt.show()

img1 = img_dark.copy()
img1 = normalHist(img1)
imgshow = plt.imshow(img1)
plt.show()
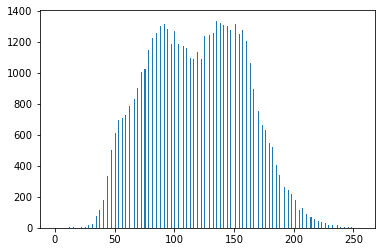
hist1 = plt.hist(img1.reshape(-1),bins=255,rwidth=0.85,range=(0,255))

2.直方图平坦化(evenHist)

调整直方图的平均值和标准差
$$x_{out}=\frac{s_0}{s}(x_{in}-m)+m_0$$

def evenHist(img,m0,s0):
    m = img.mean()
    s = np.sqrt(img.var())
    img = (s0/s)*(img-m)+m0
    img = img.astype(np.uint8)
    return img

imgshow = plt.imshow(img_dark)
plt.show()

img2 = img_dark.copy()
img2 = evenHist(img2,128,52)
imgshow = plt.imshow(img2)
plt.show()
hist1 = plt.hist(img2.reshape(-1),bins=255,rwidth=0.85,range=(0,255))

3.直方图均衡化(Histogram Equalization)

直方图均衡化保证在图像像素映射过程中原来的大小关系保持不变，即较亮的区域依旧较亮，较暗的依旧较暗，只是对比度增加，不能明暗颠倒；保证像素映射函数的值域在0和255之间。

按照以下步骤对像素值进行处理：

1. 对图像中的像素点进行统计，统计每个像素值对应的个数和占比

2. 进行函数映射，zmax是映射范围，一般为255。h(i)的累加是灰度值的累计像素个数。S是像素点个数
   $$Z^{\prime }=Z_{max}\frac{\sum _{i=0}^{z}h(i)}{S}$$

计算方法就是用当前灰度值的累计像素个数乘上要分布映射的范围(255)

1. 比如100个像素点，其中像素值最小为3，个数为5个，（sum(3) = 5）

2. 那么就把像素值为3的像素点值改为 $255\times (\frac{5}{100})=12.75$ -> 取整 -> 13

3. 下一个像素值为4，个数有8个，那么sum(4) = 5+8 = 12

4. 把像素值为4的像素点值改为 $255\times (\frac{12}{100})=30.6$ ----> 取整 ----> 31

依次累加计算像素值

def equalHist(img):
    result = np.zeros_like(img)
    #像素总数
    imgsize = img.size
    #统计0~255的值的个数
    count = np.bincount(img.reshape(-1))
    
    for i in range(count.size):
        #如果这个像素值的个数不为0（就是存在该像素值的点）
        if count[i]:
            #计算累计个数
            sum = count[:i+1].sum()
            x = 255*(sum/imgsize)
            #四舍五入后转为uint8类型
            x = np.around(x).astype(np.uint8)
            #修改原本的像素值，改动放到新的图片上，以免打乱后面的像素值运算
            result[img == i] = x
    
    return result

imgshow = plt.imshow(img)
plt.show()

img3 = img.copy()
img3 = equalHist(img3)
imgshow = plt.imshow(img3)
plt.show()
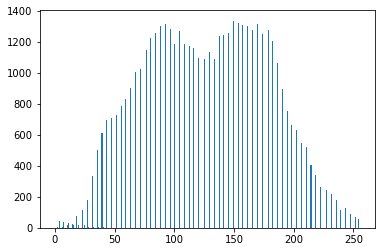
hist1 = plt.hist(img3.reshape(-1),bins=255,rwidth=0.85,range=(0,255))

4.伽马矫正(Gamma Correction)

伽马矫正用于调整图片的亮度。

由于照相机拍摄的图片在显示器上显示较暗。所以要进行伽马矫正。

矫正方法(c为常数，$\gamma$为伽马指数)：

$$归一化：x_{normal}=x_{in}/255$$
$$伽马矫正：x_{gamma}=\frac{1}{c}\cdot x_{normal}^{\frac{1}{\gamma }}$$
$$反归一化：x_{out}=x_{gamma}\cdot 255$$

假设图像中有一个像素，值是 200 ，那么对这个像素进行校正必须执行如下步骤：

1. 归一化 ：将像素值转换为 0 ～ 1 之间的实数。 算法如下 : ( i + 0. 5)/256 这里包含 1 个除法和 1 个加法操作。对于像素 A 而言 , 其对应的归一化值为 0. 783203 。

2. 预补偿 ：根据公式 , 求出像素归一化后的 数据以 1 /gamma 为指数的对应值。这一步包含一个 求指数运算。若 gamma 值为 2. 2 , 则 1 /gamma 为 0. 454545 , 对归一化后的 A 值进行预补偿的结果就 是 0. 783203 ^0. 454545 = 0. 894872 。

3. 反归一化 ：将经过预补偿的实数值反变换为 0 ～ 255 之间的整数值。具体算法为 : f*256 - 0. 5 此步骤包含一个乘法和一个减法运算。续前例 , 将A的预补偿结果 0. 894872代入上式,得到A预补偿后对应的像素值为228,这个 228 就是最后送入显示器的数据。

def gammaCorrection(img,gamma,c = 1):
    img_normal = (img+0.01)/255
    img_gamma = (1/c)*np.power(img_normal,(1/gamma))
    img_out = img_gamma*255 - 0.01
    #防止溢出
    img_out = np.clip(img_out, 0, 255)
    result = img_out.astype(np.uint8)
    return result

imgshow = plt.imshow(img_gamma)
plt.show()

img4 = img.copy()
img4 = gammaCorrection(img4,1)
imgshow = plt.imshow(img4)
plt.show()

参考输出的图片过暗，感觉gamma=1正好符合输出效果，而2.2则过亮

5.最邻近插值(Nearest-neighbor Interpolation)

将放大后的像素点位置设为近邻点的像素值，达到粗劣的放大效果,$\alpha$为放大比例
$$I^{\prime }(x,y)=I([\frac{x}{\alpha }],[\frac{y}{\alpha }])$$

def nnInterpolation(img,a):
    newshape = [int(img.shape[0]*a),int(img.shape[1]*a),img.shape[2]]
    result = np.zeros((newshape))
    for x in range(newshape[0]):
        for y in range(newshape[1]):
            x_a = int(np.floor(x/a))
            y_a = int(np.floor(y/a))
            result[x,y] = img[x_a,y_a]
    
    result = result.astype(np.uint8)
    return result

imgshow = plt.imshow(img)
plt.show()

img5 = img.copy()
img5 = nnInterpolation(img5,1.5)
imgshow = plt.imshow(img5)
plt.show()

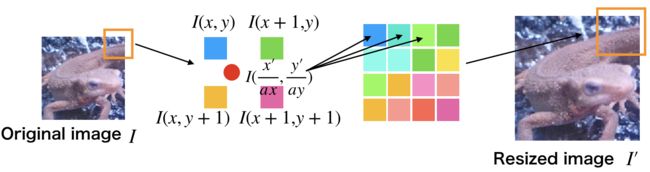
6.双线性插值(Billnear Interpolation)

使用双线性插值将图像放大$1.5$倍吧！

双线性插值考察$4$邻域的像素点，并根据距离设置权值。虽然计算量增大使得处理时间变长，但是可以有效抑制画质劣化。

1. 放大后图像的座标$(x^{\prime },y^{\prime })$除以放大率$a$，可以得到对应原图像的座标$(\lfloor \frac{x^{\prime }}{a}\rfloor ,\lfloor \frac{y^{\prime }}{a}\rfloor )$。

2. 求原图像的座标$(\lfloor \frac{x^{\prime }}{a}\rfloor ,\lfloor \frac{y^{\prime }}{a}\rfloor )$周围$4$邻域的座标$I(x,y)$，$I(x+1,y)$，$I(x,y+1)$，$I(x+1,y+1)$：

3. 分别求这4个点与$(\frac{x^{\prime }}{a},\frac{y^{\prime }}{a})$的距离，根据距离设置权重：$w=\frac{d}{\sum d}$

4. 根据下式求得放大后图像$(x^{\prime },y^{\prime })$处的像素值：

$$\begin{gathered} d_x=\frac{x^{\prime }}{a}-x \\ {d}_y=\frac{y^{\prime }}{a}-y \\ {I}^{\prime }(x^{\prime },y^{\prime })=(1-d_x)(1-d_y)I(x,y)+d_x(1-d_y)I(x+1,y)+(1-d_x)d_{y}I(x,y+1)+d_x{d}_{y}I(x+1,y+1) \end{gathered}$$

双线性插值是将原图像(oldimg)进行伸缩旋转变化之后得到新图像(newimg),将新图像像素点的位置映射回到原图像上，坐标值可能不会是整数，但是我们能获得这个点最近的四个点，通过这四个点进行计算。

1.现在假设一张图放大两倍。

2.在新图像上，我们想计算点A(1,1)的像素值，先将这个点映射到原图像上，得到的坐标是（0.5,0.5）

3.计算(0.5,0.5)最近的四个点: a1(0,0),a2(0,1),a3(1,0),a1(0,1)，代入公式即可。

def bnInterprolation(img,a):
    newshape = [int(img.shape[0]*a),int(img.shape[1]*a),img.shape[2]]
    result = np.zeros((newshape))
    #遍历新的图像坐标
    for x in range(newshape[0]):
        for y in range(newshape[1]):
            #对应的原图像上的点(向下取整，也就是左上点的位置)
            x0 = int(np.floor(x/a))
            y0 = int(np.floor(y/a))
            #新图像的坐标/放缩比例 - 原图像坐标点 = 距离
            dx = x/a-x0
            dy = y/a-y0
            
            #防止溢出
            x1 = x0+1 if x0<img.shape[0]-1 else x0
            y1 = y0+1 if y0<img.shape[1]-1 else y0   
            result[x,y] = (1-dx)*(1-dy)*img[x0,y0]+dx*(1-dy)*img[x1,y0]\
                            +(1-dx)*dy*img[x0,y1]+dx*dy*img[x1,y1]
            
    result = result.astype(np.uint8)
    return result   

imgshow = plt.imshow(img)
plt.show()

img6 = img.copy()
img6 = bnInterprolation(img6,1.5)
imgshow = plt.imshow(img6)
plt.show()

7.双三次插值（ Bicubic Interpolation ）

使用双三次插值将图像放大$1.5$倍吧！

双三次插值是双线性插值的扩展，使用邻域$16$像素进行插值。

各自像素间的距离由下式决定：
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ d_{x_1} = |\fr…
权重由基于距离的函数取得。$a$在大部分时候取$-1$。大体上说，图中蓝色像素的距离$|t|\le 1$，绿色像素的距离$1<|t|\le 2$：
$$h(t)=\{\begin{array}{ll}(a+2)|t{|}^3-(a+3)|t{|}^2+1& \text{when}|t|\le 1\\ a|t{|}^3-5a|t{|}^2+8a|t|-4a& \text{when}1<|t|\le 2\\ 0& \text{else}\end{array}$$
利用上面得到的权重，通过下面的式子扩大图像。将每个像素与权重的乘积之和除以权重的和。
$$I^{\prime }(x^{\prime },y^{\prime })=\frac{1}{\sum _{j=1}^4\sum _{i=1}^{4}h(d_{xi})h(d_{yj})}\sum _{j=1}^4\sum _{i=1}^{4}I(x+i-2,y+j-2)h(d_{xi})h(d_{yj})$$

#权重计算公式
def weight(absd):
    weights = np.zeros_like(absd)
    a = -1
    #先计算距离为0~1的点的权重
    w = (a+2)*np.power(absd,3) - (a+3)*np.square(absd) + 1
    weights[absd <= 1] = w[absd <= 1]
    #再计算距离为1~2的点的权重
    w = a*np.power(absd,3) - 5*a*np.square(absd) + 8*a*absd -4*a
    weights[(absd > 1)*(absd <= 2)] = w[(absd > 1)*(absd <= 2)]
    #其余的都为0
    return weights

def bicInterpolation(img,a):

    max_x,max_y,_ = img.shape
    #将新图像的x的坐标点映射回原图像,所以每个点的坐标为（x[i,j],y[i,j]）
    list = np.arange(img.shape[0]*a)/a
    y = np.tile(list,list.shape[0]).reshape(list.shape[0],-1)
    x = y.T
    #映射点（图中红点）对应的左上角蓝点坐标
    x0 = np.floor(x)
    y0 = np.floor(y)

    #其他15个点的坐标
    xx = np.array([np.maximum(x0-1,0),x0,np.minimum(x0+1,max_x-1),np.minimum(x0+2,max_x-1)])

    yy = np.array([np.maximum(y0-1,0),y0,np.minimum(y0+1,max_y-1),np.minimum(y0+2,max_y-1)])
    # 前面的对应的映射点的坐标(带小数)
    #而后面对应的周围16点的坐标。相减取绝对值得到距离
    #用maximun限定坐标下限(0)，用minmun限定坐标上限(max)防止溢出
    dx = np.abs(x-xx)
    dy = np.abs(y-yy)

    wx = weight(dx)
    wy = weight(dy)

    #初始化联合权重和输出(3,192,192)
    #联合权重  = 将距离代入权重函数后横纵权重相乘再累加，公式见题
    h_sum = np.zeros((img.shape[2],int(img.shape[0]*a),int(img.shape[1]*a)))
    i_sum = np.zeros_like(h_sum)
    for i in range(4):
        for j in range(4):
            #像素值
            x = img[xx[i].astype(np.int),yy[i].astype(np.int)]
            #旋转一下维度，让通道变为第一维，方便矩阵相乘
            x = x.transpose(2,0,1)
            #联合权重，扩充成3维，方便计算
            w_xy = wx[i]*wy[j]
            wxy = np.array([w_xy,w_xy,w_xy])
            h_sum += w_xy
            
            #联合权重在乘上对应的像素值
            i_sum += (x*w_xy)
    
    #相除得到结果，再把通道放回第三维
    result = (i_sum/h_sum).transpose(1,2,0)
    result = np.clip(result, 0, 255)
    result = result.astype(np.uint8)
    
    return result

imgshow = plt.imshow(img)
plt.show()

img7 = img.copy()
img7 = bicInterpolation(img7,10)
imgshow = plt.imshow(img7)
plt.show()

8.仿射变换（ Afine Transformations ）——平行移动

利用仿射变换让图像在$x$方向上$+30$，在$y$方向上$-30$吧！

仿射变换利用$3\times 3$的矩阵来进行图像变换。

变换的方式有平行移动（问题二十八）、放大缩小（问题二十九）、旋转（问题三十）、倾斜（问题三十一）等。

原图像记为$(x,y)$，变换后的图像记为$(x^{\prime },y^{\prime })$。

图像放大缩小矩阵为下式：
$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$
另一方面，平行移动按照下面的式子计算：
$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}{t}_x\\ t_y\end{array}\right)$$
把上面两个式子盘成一个：
$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{ccc}a& b& t_x\\ c& d& t_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$

平行移动操作使用下面的式子计算。$t_x$和$t_y$是像素移动的距离。
$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$

def transformations(img,mtrix):
    result = np.zeros_like(img)
    
    #将图像的坐标点保存
    list = np.arange(img.shape[1]).reshape(-1,1)
    x = np.tile(list,img.shape[0])
    list = np.arange(img.shape[0])
    y = np.tile(list,img.shape[1]).reshape(-1,img.shape[0])
    
    #仿射变换矩阵
    v = np.array([x.reshape(-1),y.reshape(-1),np.ones((x.size))])
    new_xy = np.dot(mtrix,v)
    new_xy = new_xy[0:2].astype(np.uint8)
    
    #将溢出部分去除
    out = (new_xy[1]<result.shape[0])*(new_xy>=0)*(new_xy[0]<result.shape[1])
    out = np.multiply(out[0],out[1])
    for i,flag in enumerate(out):
        #只计算未溢出部分
        if flag:
            #将原来的图像赋值到新图像
            result[new_xy[1,i],new_xy[0,i]] = img[y.reshape(-1)[i],x.reshape(-1)[i]]
    return result

def transMtrix(a,b,c,d,tx,ty):
    mtrix = np.array([[a,b,tx],[c,d,ty],[0,0,1]])
    return mtrix

imgshow = plt.imshow(img)
plt.show()

img8 = img.copy()
m = transMtrix(1,0,0,1,30,-30)
img8 = transformations(img8,m)
imgshow = plt.imshow(img8)
plt.show()

8.仿射变换（ Afine Transformations ）——放大缩小

1. 使用仿射变换，将图片在$x$方向上放大$1.3$倍，在$y$方向上缩小至原来的$\frac{4}{5}$。
2. 在上面的条件下，同时在$x$方向上向右平移$30$（$+30$），在$y$方向上向上平移$30$（$-30$）。

方法使用逆仿射变换法，将新的坐标点代入公式求得对应的原坐标点
$$\left(\begin{array}{c}x\\ y\end{array}\right)=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)-\left(\begin{array}{c}{t}_x\\ t_y\end{array}\right)$$

def AfineTrans(img,a,b,c,d,tx,ty):
    result = np.zeros((int(img.shape[0]*d),int(img.shape[1]*a),img.shape[2]))

    #将新图像的横坐标和竖坐标保存到数组中
    list = np.arange(result.shape[1]).reshape(-1,1)
    new_x = np.tile(list,result.shape[0])
    list = np.arange(result.shape[0])
    new_y = np.tile(list,result.shape[1]).reshape(-1,result.shape[0])

    #逆仿射变换求出对应的点
    ad_bc = a*d-b*c
    x = (((d*new_x)-(b*new_y))/ad_bc).astype(np.uint8)
    y = (((-c*new_x)+(a*new_y))/ad_bc).astype(np.uint8)
    
    #将原坐标的点输入到新坐标中
    result[new_y,new_x] = img[y,x]
    result = result.astype(np.uint8)
    
    m = transMtrix(1,0,0,1,tx,ty)
    result = transformations(result,m)
    return result

imgshow = plt.imshow(img)
plt.show()

img9 = img.copy()
img9 = AfineTrans(img9,1.3,0,0,0.8,30,-30)
imgshow = plt.imshow(img9)
plt.show()

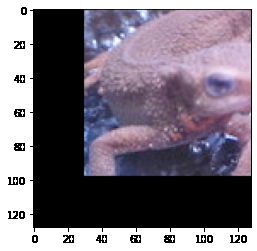
10.仿射变换（ Afine Transformations ）——旋转

1. 使用仿射变换，逆时针旋转$30$度。
2. 使用仿射变换，逆时针旋转$30$度并且能让全部图像显现（也就是说，单纯地做仿射变换会让图片边缘丢失，这一步中要让图像的边缘不丢失，需要耗费一些工夫）。

我偷懒了！直接把边缘去掉了，我有罪。。。

使用下面的式子进行逆时针方向旋转$A$度的仿射变换：
$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{ccc}\cos (A)& -\sin (A)& t_x\\ \sin (A)& \cos (A)& t_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$

def AfineTrans2(img,a,b,c,d,tx,ty):
    #边缘去掉方便计算
    img[0,:] = 0
    img[-1,:] = 0
    img[:,0] = 0
    img[:,-1] = 0
    
    result = np.zeros_like(img)
    #将新图像的横坐标和竖坐标保存到数组中
    list = np.arange(result.shape[0])
    new_x = np.tile(list,result.shape[1]).reshape(-1,result.shape[0])
    list = np.arange(result.shape[1]).reshape(-1,1)
    new_y = np.tile(list,result.shape[0])
    #逆仿射变换求出对应的点
    ad_bc = a*d-b*c
    x = np.round((d*new_x-b*new_y)/ad_bc).astype(np.int)-tx
    y = np.round((-c*new_x+a*new_y)/ad_bc).astype(np.int)-ty
    
    x = np.minimum(np.maximum(x, 0), img.shape[0]-1).astype(np.uint8)
    y = np.minimum(np.maximum(y, 0), img.shape[1]-1).astype(np.uint8)

    #将原坐标的点输入到新坐标中
    result[new_x,new_y] = img[x,y]
    result = result.astype(np.uint8)

    return result

imgshow = plt.imshow(img)
plt.show()

img10 = img.copy()
cc = 30*np.pi/180
img10 = AfineTrans2(img10,np.cos(cc),-np.sin(cc),np.sin(cc),np.cos(cc),20,-40)
imgshow = plt.imshow(img10)
plt.show()

这次的十个题目感觉比之前的硬核很多，要仔细研究，话说回来扎实的基础也挺重要的

---

原创首发，欢迎来我的博客留言讨论，我的博客主页：LeonG是什么意思？我的知乎专栏：LeonG与机器学习

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。