python实战之泰坦尼克号获救问题

数据来源：
Kaggle数据集 →
共有1309名乘客数据，其中891是已知存活情况（train.csv），剩下418则是需要进行分析预测的（test.csv）
字段意义：
PassengerId: 乘客编号
Survived :存活情况（存活：1 ; 死亡：0）
Pclass : 客舱等级
Name : 乘客姓名
Sex : 性别
Age : 年龄
SibSp : 同乘的兄弟姐妹/配偶数
Parch : 同乘的父母/小孩数
Ticket : 船票编号
Fare : 船票价格
Cabin :客舱号
Embarked : 登船港口
目的：通过已知获救数据，预测乘客生存情况研究问题：
1、整体来看，存活比例如何？
要求：① 读取已知生存数据train.csv② 查看已知存活数据中，存活比例如何？
提示：① 注意过程中筛选掉缺失值之后再分析② 这里用seaborn制图辅助研究
2、结合性别和年龄数据，分析幸存下来的人是哪些人？
要求：① 年龄数据的分布情况② 男性和女性存活情况③ 老人和小孩存活情况
3、结合 SibSp、Parch字段，研究亲人多少与存活的关系
要求：① 有无兄弟姐妹/父母子女和存活与否的关系② 亲戚多少与存活与否的关系
4、结合票的费用情况，研究票价和存活与否的关系
要求：① 票价分布和存活与否的关系② 比较研究生还者和未生还者的票价情况
5、利用KNN分类模型，对结果进行预测
要求：① 模型训练字段：‘Survived’,‘Pclass’,‘Sex’,‘Age’,‘Fare’,'Family_Size’②模型预测test.csv样本数据的生还率
提示：① 训练数据集中，性别改为数字表示 → 1代表男性，0代表女性

泰坦尼克号获救问题十分经典，比较初级，不过也很有练习价值。在这里我也简单记录一下自己的思路，小小分享，欢迎指正。
拿到问题，先打开数据看一看，了解一下大概情况以及分析目的。
前四问很简单，需要对数据进行描述、评判，最后一问是利用模型进行简单的预测。整体难度不高。

1 导入模块，加载数据

根据题目要求，预测需要的模块，也可以后期用到再加。然后导入数据，查看具体情况。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
import time

import warnings
warnings.filterwarnings('ignore')

os.chdir('/Users/eleven/Desktop/python/泰坦尼克号获救问题/')
train_data = pd.read_csv('train.csv')
test_data = pd.read_csv('test.csv')

2 查看存活比例

存活只有两个数据值，1和0，可以直接用饼状图来体现，简单直观。

sns.set()
sns.set_style('ticks')
plt.axis('equal')
survive_per = train_data['Survived'].value_counts()
survive_per.plot.pie(autopct = '%.2f%%')

用seaborn制图，设置为正方形的绘图空间，通过value_counts计数，生成pie饼状图

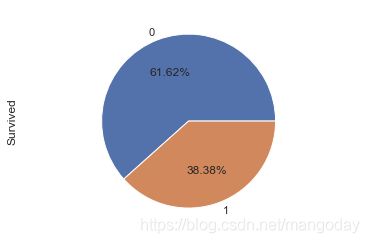
得到存活比例为38.38%。

3 分析幸存下来的人群分布

（1）年龄数据的分布情况

简单的看分布情况，可以用直方图和箱型图来表示。

train_data_age = train_data[train_data['Age'].notnull()]
#去除缺失值

plt.figure(figsize = (12,6))
plt.subplot(121)
train_data_age['Age'].hist(bins = 70)
plt.xlabel('age')
plt.ylabel('num')
#绘制直方图

plt.subplot(122)
train_data.boxplot(column = 'Age',showfliers = False)
#绘制箱型图

train_data_age['Age'].describe()
#数据描述

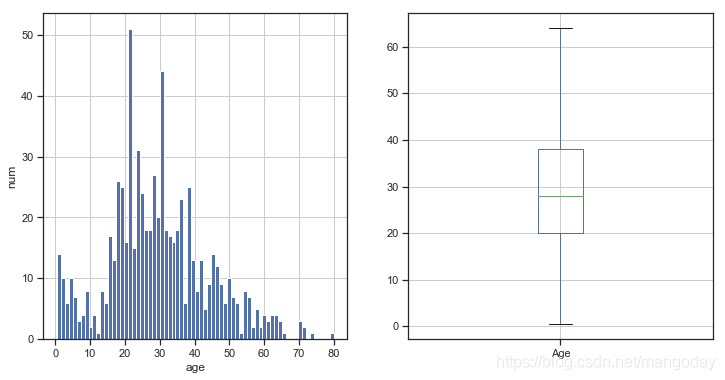
可以得到年龄分布情况：去掉缺失值后共714位，平均年龄约30岁，标准差约14岁，最小年龄0.42，最大年龄80。

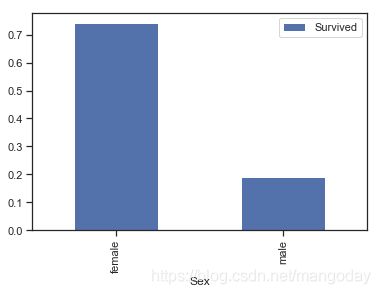
（2）男性和女性存活情况

因为survived仅存在0和1两个值，因此想得到存活率，直接求字段平均值即可。

survive_sex = train_data[['Sex','Survived']].groupby('Sex').mean()
survive_sex.plot.bar()

print('女性存活率为%.2f%%，男性存活率为%.2f%%' 
      % (survive_sex.loc['female']*100,survive_sex.loc['male']*100))

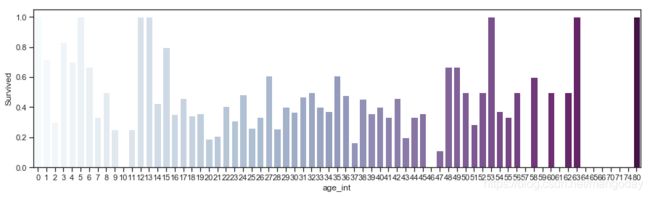
（3）老人和小孩存活情况

在这里为了直观一些，我们直接对年龄值进行处理变为整型，然后分别查看每个年龄值的存活率并作图。

plt.figure(figsize = (15,4))
train_data_age['age_int'] = train_data_age['Age'].astype(int)
average_age = train_data_age[['age_int','Survived']].groupby(['age_int'],as_index = False).mean()
sns.barplot(x = 'age_int',y = 'Survived',data = average_age,palette = 'BuPu')

4 结合 SibSp、Parch字段，研究亲人多少与存活的关系

（1）有无兄弟姐妹/父母子女和存活与否的关系

根据题目要求，分四种情况（有无兄弟，有无父母）计算存活率。
先进行数据筛选。

sib_data = train_data[train_data['SibSp'] != 0]
nosib_data = train_data[train_data['SibSp'] == 0]
par_data = train_data[train_data['Parch'] != 0]
nopar_data = train_data[train_data['Parch'] == 0]

为了表现更直观一些，分情况作饼图。其实用饼图、柱状图都可以。

plt.figure(figsize = (12,4))
plt.subplot(141)
plt.axis('equal')
sib_data['Survived'].value_counts().plot.pie(labels = ['No Survived','Survived'],autopct = '%.2f%%',colormap = 'Blues')
plt.xlabel('sibsp')

plt.subplot(142)
plt.axis('equal')
nosib_data['Survived'].value_counts().plot.pie(labels = ['No Survived','Survived'],autopct = '%.2f%%',colormap = 'Blues')
plt.xlabel('no_sibsp')
#有无兄弟姐妹的存活率对比

plt.subplot(143)
plt.axis('equal')
par_data['Survived'].value_counts().plot.pie(labels = ['No Survived','Survived'],autopct = '%.2f%%',colormap = 'Reds')
plt.xlabel('parch')

plt.subplot(144)
plt.axis('equal')
nopar_data['Survived'].value_counts().plot.pie(labels = ['No Survived','Survived'],autopct = '%.2f%%',colormap = 'Reds')
plt.xlabel('no_parch')
#有无父母子女的存活率对比

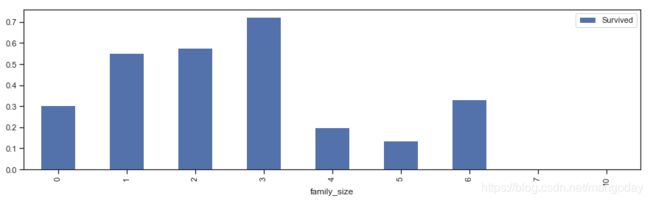
（2）亲戚多少与存活与否的关系

Parch和SibSp两个字段相加其实就是亲戚个数，直接分组求平均值看存活率。

train_data['family_size'] = train_data['Parch'] + train_data['SibSp']
train_data[['family_size','Survived']].groupby('family_size').mean().plot.bar(figsize = (15,4))
#查看亲戚个数与存活率

5 结合票的费用情况，研究票价和存活与否的关系

这里的思路其实也可以和之前的一样，就是分票价查看存活率。但是我们浏览票价发现票价并不是统一的几个值，这里可以先作图看看票价分布。

fig,ax = plt.subplots(1,2,figsize = (15,4))
train_data['Fare'].hist(bins = 70,ax = ax[0])
train_data.boxplot(column = 'Fare',by = 'Pclass', showfliers=False,ax = ax[1])
#查看票价分布

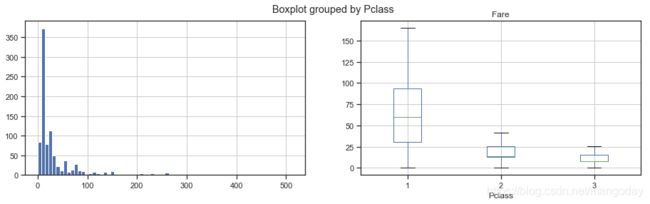
那么可以换一个思路了，反过来通过查看生还和死亡人群的票价分布，了解情况。

fare_die = train_data['Fare'][train_data['Survived'] == 0]
fare_sur = train_data['Fare'][train_data['Survived'] == 1]

average_fare = pd.DataFrame([fare_die.mean(),fare_sur.mean()])
std_fare = pd.DataFrame([fare_die.std(),fare_sur.std()])
average_fare.plot(yerr = std_fare,kind = 'bar',legend = False,figsize = (12,6),grid = True)

6 利用KNN分类模型，对结果进行预测

KNN，可以理解为由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。首先查看训练字段，进行训练数据清洗，将字段数据矢量化。

#数据清洗
knn_train = train_data[['Survived','Pclass','Sex','Age','Fare','family_size']].dropna()
knn_train['Sex'][knn_train['Sex'] == 'male'] = 1
knn_train['Sex'][knn_train['Sex'] == 'female'] = 0
#性别改为数字表示

接下来要处理预测数据，保证字段相同。

test_data['family_size'] = test_data['Parch'] + test_data['SibSp']
knn_test = test_data[['Pclass','Sex','Age','Fare','family_size']].dropna()
knn_test['Sex'][knn_test['Sex'] == 'male'] = 1
knn_test['Sex'][knn_test['Sex'] == 'female'] = 0
#处理预测数据

第三步就是导入模块，构建模型，进行预测了。

from sklearn import neighbors
#导入KNN分类模块

knn = neighbors.KNeighborsClassifier()
knn.fit(knn_train[['Pclass','Sex','Age','Fare','family_size']],knn_train['Survived'])
#构建模型

knn_test['predict'] = knn.predict(knn_test)
#预测结果

shl = len(knn_test[knn_test['predict'] == 1])/len(knn_test)
print('预测生还率为%.2f%%'%(shl*100))

knn_sur = knn_test[knn_test['predict'] == 1].reset_index()
del knn_sur['index']
#得到具体存活情况

得到预测生还率为38.07%，以及生还样本的具体数据。