JAVA算法:DFS算法题解两个例子(走迷宫和求排列组合数)
DFS算法题解两个例子(走迷宫和求排列组合数)
用DFS算法来求解几道题目。典型的问题是走迷宫问题。
####走迷宫题目描述
给定一个M*N的矩阵(二维数组),分别用0和1表示通路和障碍物。即 0 表示 通路;1 表示 障碍物。从矩阵的左上角开始,每次只能向右,下,左,上移动位置,不能斜着走。请给出从入口到出口的路线。
怎么开始思考呢?
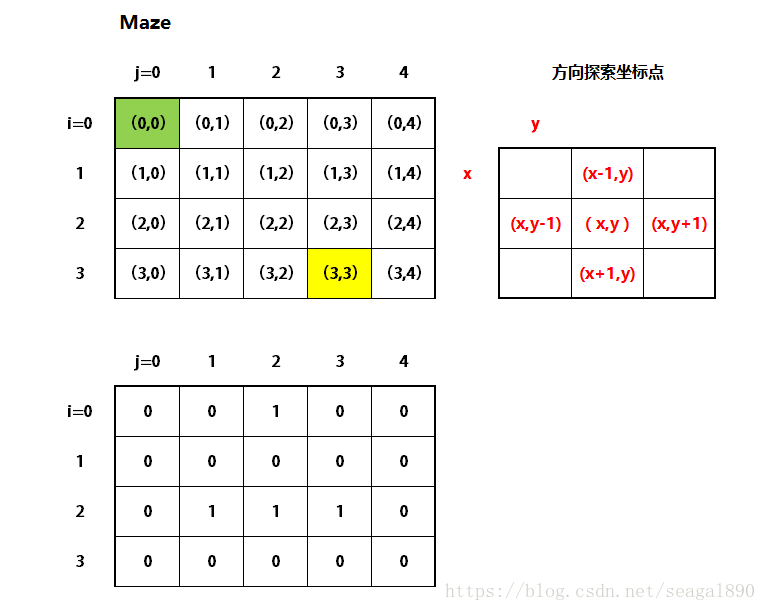
首先想想,这个题目其实是找从入口(Entrance)到出口(Exit)的可能的路径。矩阵(二维数组)从左上角开始,坐标为(0,0),可以向右走,坐标为(0,1);或者向下走,坐标为(1,0)。对于一般的位置(x,y),可以有4个搜索方向:右(x,y+1),下(x+1,y),左(x,y-1),上(x-1,y)。
如何设计DFS搜索函数呢?
二维数组(M行,N列)的右下角出口位置可以表示为:(m-1, n-1)
路径表示为path ; 但是路径可能有很多条,其中最短的路径表示为:shortestPath。
至少这个函数需要三个参数。dfs(x坐标,y坐标,搜索矩阵即二维数组)
所定义dfs函数为:
public static void dfsMaze(int x,int y, int[][] maze)
然后设计搜索结束返回的判断条件
//设置结束条件
if (x < 0 || y < 0)
return;
// 如果坐标越界,或者 maze[x][y]==1 表示遇到障碍
if (x > m - 1 || y > n - 1 || maze[x][y] ==1)
return;
//表示遇到障碍
if (maze[x][y] == 1)
return; // 判断是否通路和越界
判断是否达到出口位置
if (x == m - 1 && y == n - 1) { // 判断是否抵达出口
path = path + "(" + x + "," + y + ")";
if (shortestPath.length() == 0 || shortestPath.length() > shortestPath.length())
shortestPath = path;
System.out.println("找到路线:" + path);
return;
}
对于任意位置(二维数组的某一个位置)因为0代表通路,1代表障碍物,如果走过了可以到达的位置,将其设定一个标记为1
maze[x][y] = 1; // 将走过的路标记。当改路线搜索完成时,再清除此标记为0。
搜索方向可以表示为:
// 向四个方向搜索
dfsMaze(x + 1, y, maze); //向右搜索
dfsMaze(x, y + 1, maze); //向下搜索
dfsMaze(x, y - 1, maze); //向上搜索
dfsMaze(x - 1, y, maze); //向左搜索
它表示从上一个位置开始,向下一个位置搜索的坐标。
完整的代码如下所示:
package com.bean.algorithmbasic;
public class DFSMaze {
/**
* DFS算法解决走迷宫问题
* 0: 表示通路
* 1: 表示死路
*
*/
static String path = "";
static String shortestPath = "";
public static void dfsMaze(int x, int y, int[][] maze) {
/*
* 获得矩阵的大小
* */
int m=maze.length;
int n=maze[0].length;
//设置结束条件
if (x < 0 || y < 0)
return;
// 如果坐标越界,或者 maze[x][y]==1 表示遇到障碍
if (x > m - 1 || y > n - 1 || maze[x][y] ==1)
return;
//表示遇到障碍
if (maze[x][y] == 1)
return; // 判断是否通路和越界
if (x == m - 1 && y == n - 1) { // 判断是否抵达出口
path = path + "(" + x + "," + y + ")";
if (shortestPath.length() == 0 || shortestPath.length() > shortestPath.length())
shortestPath = path;
System.out.println("找到路线:" + path);
return;
}
String temp = path;
path = path + "(" + x + "," + y + ")" + "-"; // 记录路线
maze[x][y] = 1; // 将走过的路标记
// 向四个方向搜索
dfsMaze(x + 1, y, maze); //向右搜索
dfsMaze(x, y + 1, maze); //向下搜索
dfsMaze(x, y - 1, maze); //向上搜索
dfsMaze(x - 1, y, maze); //向左搜索
// 将路线和标记恢复成上一次的状态
maze[x][y] = 0;
//清除
path = temp;
}
public static void main(String[] args) {
// 初始化一个迷宫地图
// 0: 表示通路
// 1:表示死路
int[][] maze = {
{0, 0, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 1},
{1, 0, 1, 1, 0, 1, 1, 0, 1},
{1, 0, 1, 0, 0, 1, 0, 0, 1},
{1, 0, 1, 0, 1, 0, 1, 0, 1},
{1, 0, 0, 0, 0, 0, 1, 0, 1},
{1, 1, 0, 1, 1, 0, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 0},
{1, 1, 1, 1, 1, 1, 1, 1, 0}
};
int[][] maze2 = {
{0, 0, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 1},
{1, 0, 1, 1, 0, 1, 1, 0, 1},
{1, 0, 1, 0, 0, 1, 0, 0, 1},
{1, 0, 1, 0, 1, 0, 1, 0, 1},
{1, 0, 0, 0, 0, 0, 1, 0, 1},
{1, 1, 0, 1, 1, 0, 1, 0, 1},
{1, 0, 0, 0, 0, 0, 1, 0, 0},
{1, 1, 1, 1, 1, 1, 1, 1, 0}
};
/*
* 从矩阵的左上角位置开始搜索
* */
dfsMaze(0, 0, maze);
if (shortestPath.length() != 0)
System.out.println("最短路线为:" + shortestPath);
else
System.out.println("没有找到路线!");
}
}
运行结果为:
找到路线:(0,0)-(0,1)-(1,1)-(2,1)-(3,1)-(4,1)-(5,1)-(5,2)-(6,2)-(7,2)-(7,3)-(7,4)-(7,5)-(7,6)-(7,7)-(7,8)-(8,8)
找到路线:(0,0)-(0,1)-(1,1)-(2,1)-(3,1)-(4,1)-(5,1)-(5,2)-(5,3)-(5,4)-(5,5)-(6,5)-(7,5)-(7,6)-(7,7)-(7,8)-(8,8)
找到路线:(0,0)-(0,1)-(1,1)-(1,2)-(1,3)-(1,4)-(2,4)-(3,4)-(3,3)-(4,3)-(5,3)-(5,4)-(5,5)-(6,5)-(7,5)-(7,6)-(7,7)-(7,8)-(8,8)
找到路线:(0,0)-(0,1)-(1,1)-(1,2)-(1,3)-(1,4)-(2,4)-(3,4)-(3,3)-(4,3)-(5,3)-(5,2)-(6,2)-(7,2)-(7,3)-(7,4)-(7,5)-(7,6)-(7,7)-(7,8)-(8,8)
最短路线为:(0,0)-(0,1)-(1,1)-(2,1)-(3,1)-(4,1)-(5,1)-(5,2)-(6,2)-(7,2)-(7,3)-(7,4)-(7,5)-(7,6)-(7,7)-(7,8)-(8,8)
这里有一个问题,如果最短的路线不只一条,怎么处理?这个算法中并没有考虑这个问题。
所以这个算法还是有一定的瑕疵的。
####求排列组合数
假设给定3个数:1,2,3,求出其所有的排列组合情况。
例如:
1,1,1
1,1,2
1,1,3
1,2,1
1,2,2
1,2,3
……
3,3,3
这个问题也可以使用DFS算法求解。
那么该如何开始思考这个问题呢?
首先定义一个数组:
int[] array = new int[3];
数组元素表示为:array[0]=1; array[1]=2;array[2]=3
这个数组代表搜索的开始。从array[0]开始,第一种情况组合就是:1,1,1
设计DFS搜索函数的原型为:
public void dfsExample(int index)
其中:参数的含义是从目标数组中依次取出第几个元素。index代表数组元素的下标。
边界条件为:
// 边界条件
if (index == 3)
{
for (int i = 0; i < 3; i++)
{
System.out.print(array[i]+" ");
}
System.out.println();
//走不下去了就 return了
return;
}
搜索过程为:
for (int i = 1; i <= 3; i++)
{
array[index] = i;
// index+1 枚举下一种情况
dfsExample(index+1);
}
完整的算法设计如下:
package com.bean.algorithmbasic;
public class DFSDemo {
int[] num = new int[3];
public void dfsExample(int index)
{
// 边界条件
if (index == 3)
{
for (int i = 0; i < 3; i++)
{
System.out.print(num[i]+" ");
}
System.out.println();
//走不下去了就 return了
return;
}
for (int i = 1; i <= 3; i++)
{
num[index] = i;
// index+1 枚举下一种情况
dfsExample(index+1);
}
}
public static void main(String[] args) {
DFSDemo dfsdemo=new DFSDemo();
dfsdemo.dfsExample(0);
}
}
输出结果如下所示:
1 1 1
1 1 2
1 1 3
1 2 1
1 2 2
1 2 3
1 3 1
1 3 2
1 3 3
2 1 1
2 1 2
2 1 3
2 2 1
2 2 2
2 2 3
2 3 1
2 3 2
2 3 3
3 1 1
3 1 2
3 1 3
3 2 1
3 2 2
3 2 3
3 3 1
3 3 2
3 3 3
这两个题目的求解结果并不重要,重要的是需要整理清楚在使用DFS算法思想求解问题时,该如何入手思考问题。
有一些思路还需要在继续思考。
(还没有完全思考清楚)
(完)