聚类分析（三） 层次聚类及matlab程序

一、层次聚类介绍
1.1 简介
层次聚类，主要是对给定的待聚类的数据集进行层次化分解。主要分为两大类：
1.从下到上的凝聚聚类
2.从上到下的分裂聚类
其他算法大部分是对样本之间距离度量或者类间凝聚/分裂依据进行改进。
1.2从下到上的凝聚算法
从下到上的凝聚算法能够让人们较为直观的观察到凝聚的树结构，也是层次聚类中比较常用的一个方法。
主要过程如下图所示。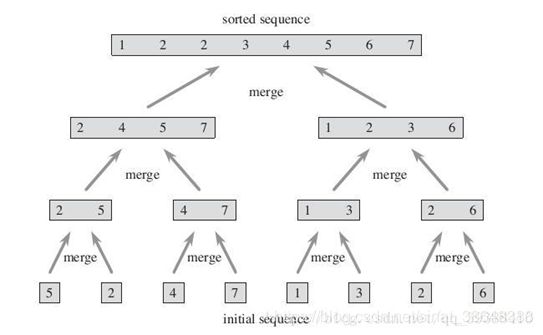

其中需要的步骤主要有三步：
1.选择变量
选择需要聚类的样本，就是需要聚类的数据集
2.计算样本之间的距离/相似度
关于样本距离的选择如果是空间变量，变量之间没有相互关系，一般选择欧式距离
如果样本之间存在物理上的关联，比如下一样本的产生与上一样本具有相同的物理原理，一般选择相似度。
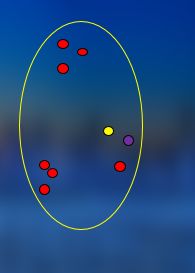
将每个样本看成一个簇，计算每一类（样本）与其他类（样本）之间的相似度/距离，将样本距离按从小到大进行排序，按照从距离/相似度距离进行不断连接。

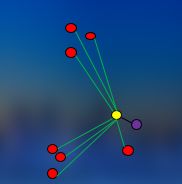
很明显黄点与紫色点聚为一类，然后可以得到6类，如下图所示，然后计算样本距离。

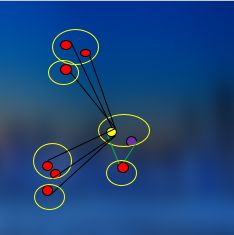
然后依据类间的聚合方式进行聚合，继续进行聚类。

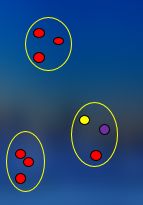
然后聚为3类。最后合并为1类。

简单来说，就是不断计算簇中样本之间的相似度/距离，然后根据选择聚合依据进行不断聚类。
3.计算类间之间的聚合方式
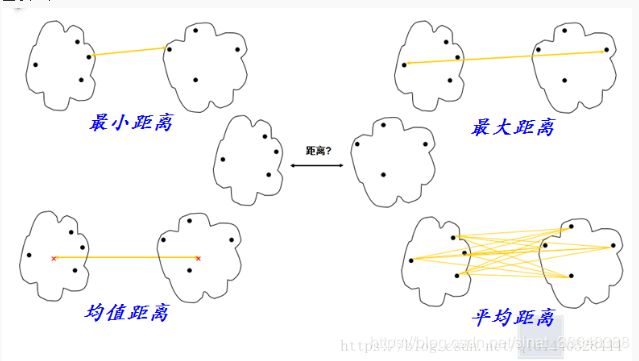
类间距离合并的依据主要有6种：
1.‘single’：单连通，最短距离法
2.‘complete’：全连通，最长距离法
3.‘average’：未加权平均距离法；
4.‘centroid’：质心距离法
5.‘median’：加权质心距离法
6. ‘ward’：内平方距离
示意图如下所示：
引自：https://www.2cto.com/net/201806/755321.html

过程图：

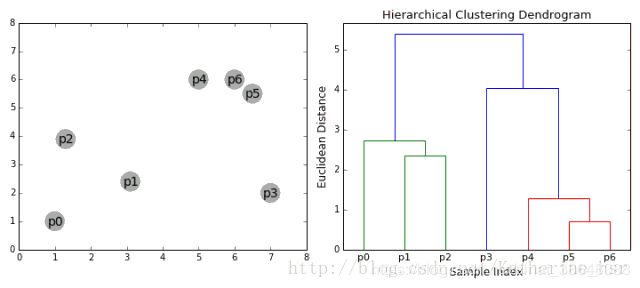
二、matlab程序
matlab中提供clusterdata函数用来进行聚类，默认返回值为每个样本的类别

hidx=clusterdata(data,'maxclust',numClust,'distance',dist_h,'linkage',link);

data为数据集
numClust为你需要聚类的个数
‘distance’,表示样本之间的距离计算方式,
dist_h 可供选择的参数有：{euclidean’：欧氏距离（默认）；‘seuclidean’：标准化欧氏距离；‘mahalanobis’：马氏距离；‘cityblock’：布洛克距离；‘minkowski’：明可夫斯基距离；
‘cosine’：余弦距离 ‘correlation’：相关性 ‘hamming’：汉明距离 ‘jaccard’：Jaccard相似度}；
‘linkage’,参数为簇间合并的依据，
link 可供选择的参数有：{single’：单连通，最短距离法（默认）；‘complete’：全连通，最长距离法；‘average’：未加权平均距离法；‘weighted’：加权平均法；‘centroid’：质心距离法；‘median’：加权质心距离法；‘ward’：内平方距离’chebychev’：Chebychev距离}。

%% 读取数据
clc;clear all,close all
pre_data=xlsread('StockFinance.xlsx','Sheet1','E2:N4735');
%% 数据归一化
[rn,cn]=size(pre_data);
step1_data=zeros(rn,cn);
   for k=1:cn
       %基于均值方差的离群点数据归一化
       xm=mean(pre_data(:,k));
       xs=std(pre_data(:,k));
       for j=1:rn
           if (pre_data(j,k))>xm+2*xs
               step1_data(j,k)=1;
           elseif (pre_data(j,k))