Python--学习笔记

Python包管理工具–PIP安装使用

wget https://bootstrap.pypa.io/get-pip.py
python get-pip.py --user

wget 命令会下载get-pip.py脚本到当前文件夹下，python get-pip.py会安装pip2 和pip3两个工具。

模块/包

glob 模块

在python中，glob模块是用来查找匹配的文件的
在查找的条件中，需要用到Unix shell中的匹配规则：

   *    :   匹配所所有
   ?    :   匹配一个字符
   *.*  :   匹配如：[hello.txt,cat.xls,xxx234s.doc]
   ?.*  :   匹配如：[1.txt,h.py]
   ?.gif:   匹配如：[x.gif,2.gif]
可以参考：fnmatch
如果没有匹配的，glob.glob(path)将返回一个空的list:[]

scipy 模块

SciPy是一个高级的科学计算库，SciPy一般都是操控NumPy数组来进行科学计算，SciPy有很多子模块可以应对不同的应用。

• scipy.cluster 向量计算 / Kmeans
• scipy.constants 物理和数学常量
• scipy.fftpack 傅里叶变换
• scipy.integrate 积分程序
• scipy.interpolate 插值
• scipy.io 数据输入和输出
• scipy.linalg 线性代数程序
• scipy.ndimage n-维图像包
• scipy.odr 正交距离回归
• scipy.optimize 优化
• scipy.signal 信号处理
• scipy.sparse 稀疏矩阵
• scipy.spatial 空间数据结构和算法
• scipy.special 一些特殊数学函数
• scipy.stats 统计

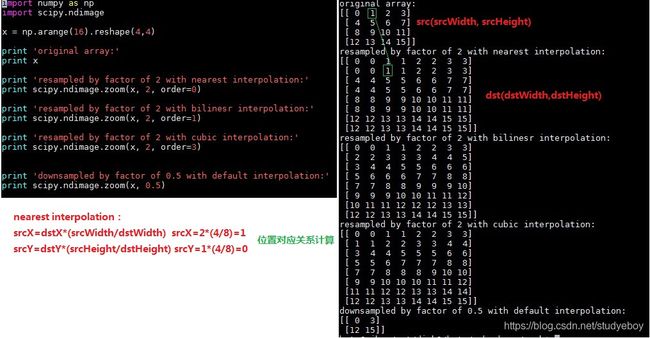
scipy.ndimage.zoom

ndimage子模块专用于图像处理。ndimage表示一个n维图像。

scipy.sparse.csr_matrix scipy.sparse.csc_matrix

csr：Compressed Sparse Row matrix
csc：Compressed Sparse Column matrix

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> sparse.csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
       [0, 0, 3],
       [4, 5, 6]])
# 按row行来压缩
# 对于第i行，非0数据列是indices[indptr[i]:indptr[i+1]] 数据是data[indptr[i]:indptr[i+1]]
# 在本例中
# 第0行，有非0的数据列是indices[indptr[0]:indptr[1]] = indices[0:2] = [0,2]
# 数据是data[indptr[0]:indptr[1]] = data[0:2] = [1,2],所以在第0行第0列是1，第2列是2
# 第1行，有非0的数据列是indices[indptr[1]:indptr[2]] = indices[2:3] = [2]
# 数据是data[indptr[1]:indptr[2] = data[2:3] = [3],所以在第1行第2列是3
# 第2行，有非0的数据列是indices[indptr[2]:indptr[3]] = indices[3:6] = [0,1,2]
# 数据是data[indptr[2]:indptr[3]] = data[3:6] = [4,5,6],所以在第2行第0列是4，第1列是5,第2列是6

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> sparse.csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])
# 按col列来压缩
# 对于第i列，非0数据行是indices[indptr[i]:indptr[i+1]] 数据是data[indptr[i]:indptr[i+1]]
# 在本例中
# 第0列，有非0的数据行是indices[indptr[0]:indptr[1]] = indices[0:2] = [0,2]
# 数据是data[indptr[0]:indptr[1]] = data[0:2] = [1,2],所以在第0列第0行是1，第2行是2
# 第1行，有非0的数据行是indices[indptr[1]:indptr[2]] = indices[2:3] = [2]
# 数据是data[indptr[1]:indptr[2] = data[2:3] = [3],所以在第1列第2行是3
# 第2行，有非0的数据行是indices[indptr[2]:indptr[3]] = indices[3:6] = [0,1,2]
# 数据是data[indptr[2]:indptr[3]] = data[3:6] = [4,5,6],所以在第2列第0行是4，第1行是5,第2行是6

numpy模块

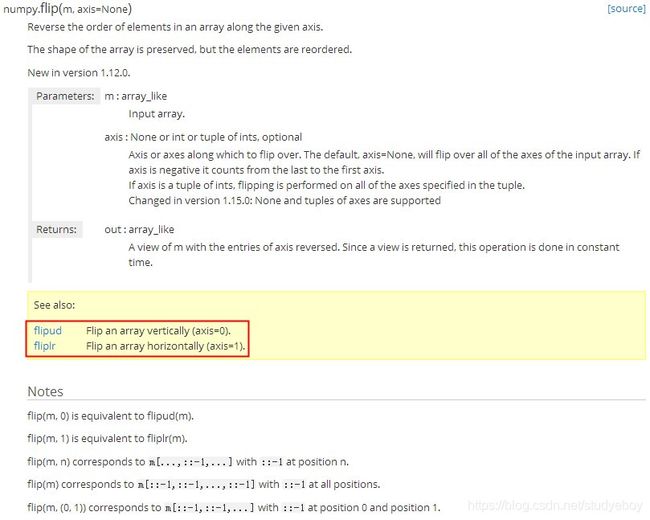
np.flip

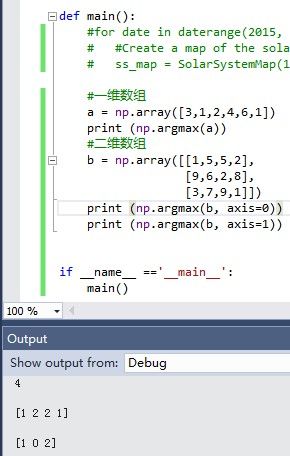
np.argmax

返回最大数的索引。有一个默认参数axis，默认是0，表示第几维的最大值。

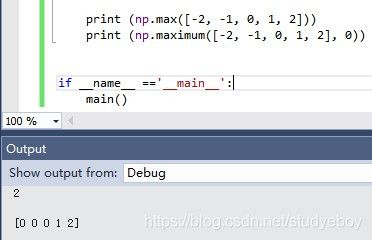
np.max

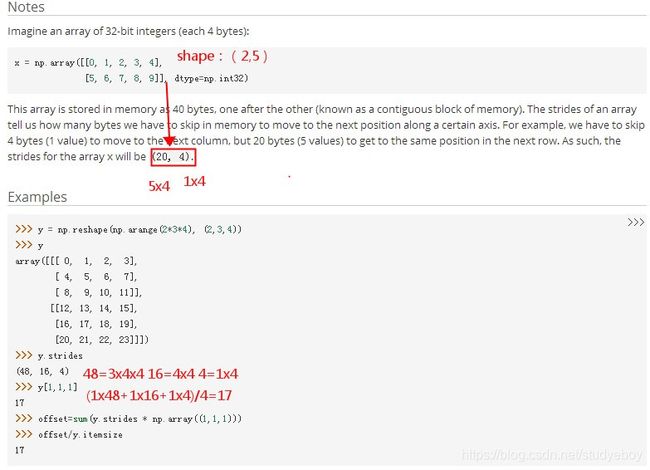
np.ndarrary.strides

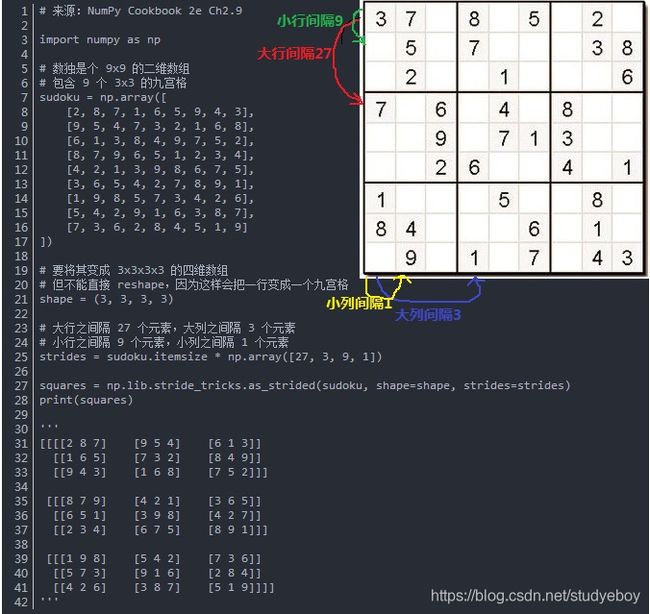
np.lib.stride_tricks.as_strided

np.ravel np.flatten np.squeeze

numpy中的ravel()、flatten()、squeeze()都有将多维数组转换为一维数组的功能，区别：

• ravel() 如果没有必要，不会产生源数据的副本，修改它会影响原来的数据
• flatten() 返回源数据的副本，修改它不会影响原来的数据
• squeenze() 只能对维数为1的维度降维
• reshape(-1) 也可以拉平多为数组
  

np.stack

# 沿着新轴连接数组的序列
numpy.stack(arrays, axis=0)
# axis 指定新轴在结果尺寸中的索引。
# arrarys 数组，array_like的序列每个数组必须具有相同的形状。
# 返回 堆叠数组比输入数组多一个维

>>> import numpy as np
>>> a = np.array([1,2,3])
>>> b = np.array([4,5,6])
>>> c = np.array([7,8,9])
>>> print (a.shape)
(3,)
>>> print (b.shape)
(3,)
>>> print(c.shape)
(3,)
>>> ab0 = np.stack((a,b),axis=0)
>>> print(ab0.shape)
(2, 3)
>>> print(ab0)
[[1 2 3]
 [4 5 6]]
>>> ab1 = np.stack((a,b), axis=1)
>>> print(ab1.shape)
(3, 2)
>>> print (ab1)
[[1 4]
 [2 5]
 [3 6]]
>>> abc0 = np.stack((a,b,c),axis=0)
>>> print(abc0.shape)
(3, 3)
>>> print(abc0)
[[1 2 3]
 [4 5 6]
 [7 8 9]]
>>> abc1 = np.stack((a,b,c),axis=1)
>>> print(abc1.shape)
(3, 3)
>>> print(abc1)
[[1 4 7]
 [2 5 8]
 [3 6 9]]
>>> abc2 = np.stack((a,b,c),axis=2)
Traceback (most recent call last):
  File "", line 1, in 
  File "C:\Program Files (x86)\Microsoft Visual Studio\Shared\Python36_64\lib\site-packages\numpy\core\shape_base.py", line 356, in stack
    axis = normalize_axis_index(axis, result_ndim)
numpy.core._internal.AxisError: axis 2 is out of bounds for array of dimension 2
>>> 

>>> a = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> b = np.array([[10,20,30],[40,50,60],[70,80,90]])
>>> c = np.array([[11,12,13],[14,15,16],[17,18,19]])
>>> print(a.shape)
(3, 3)
>>> print(a)
[[1 2 3]
 [4 5 6]
 [7 8 9]]
>>> print(b.shape)
(3, 3)
>>> print(b)
[[10 20 30]
 [40 50 60]
 [70 80 90]]
>>> print(c.shape)
(3, 3)
>>> print(c)
[[11 12 13]
 [14 15 16]
 [17 18 19]]
>>> abc0 = np.stack((a,b,c),axis=0)
>>> print(abc0.shape)
(3, 3, 3)
>>> print(abc0)
[[[ 1  2  3]
  [ 4  5  6]
  [ 7  8  9]]

 [[10 20 30]
  [40 50 60]
  [70 80 90]]

 [[11 12 13]
  [14 15 16]
  [17 18 19]]]
>>> abc1 = np.stack((a,b,c),axis=1)
>>> print(abc1.shape)
(3, 3, 3)
>>> print(abc1)
[[[ 1  2  3]
  [10 20 30]
  [11 12 13]]

 [[ 4  5  6]
  [40 50 60]
  [14 15 16]]

 [[ 7  8  9]
  [70 80 90]
  [17 18 19]]]
>>> abc2 = np.stack((a,b,c),axis=2)
>>> print(abc2.shape)
(3, 3, 3)
>>> print(abc2)
[[[ 1 10 11]
  [ 2 20 12]
  [ 3 30 13]]

 [[ 4 40 14]
  [ 5 50 15]
  [ 6 60 16]]

 [[ 7 70 17]
  [ 8 80 18]
  [ 9 90 19]]]
>>> ab0 = np.stack((a,b),axis=0)
>>> print(ab0.shape)
(2, 3, 3)
>>> print(ab0)
[[[ 1  2  3]
  [ 4  5  6]
  [ 7  8  9]]

 [[10 20 30]
  [40 50 60]
  [70 80 90]]]
>>> ab1 = np.stack((a,b),axis=1)
>>> print(ab1.shape)
(3, 2, 3)
>>> print(ab1)
[[[ 1  2  3]
  [10 20 30]]

 [[ 4  5  6]
  [40 50 60]]

 [[ 7  8  9]
  [70 80 90]]]
>>> ab2 = np.stack((a,b),axis=2)
>>> print(ab2.shape)
(3, 3, 2)
>>> print(ab2)
[[[ 1 10]
  [ 2 20]
  [ 3 30]]

 [[ 4 40]
  [ 5 50]
  [ 6 60]]

 [[ 7 70]
  [ 8 80]
  [ 9 90]]]
>>> 

np.tile

将原矩阵横向纵向的复制。

>>> mat = np.array([[1,2],[3,4]])
>>> mat0 = np.tile(mat,(1,4))
>>> print(mat0)
[[1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]]
>>> mat1 = np.tile(mat,(2,2))
>>> print(mat1)
[[1 2 1 2]
 [3 4 3 4]
 [1 2 1 2]
 [3 4 3 4]]
>>> 

np.linalg.norm

求取向量二范数，并求取单位向量（行向量计算）

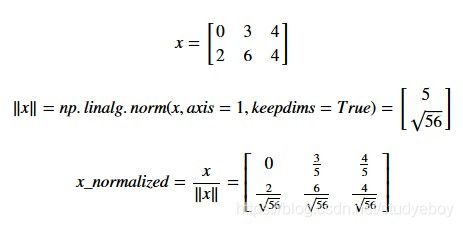
顾名思义，linalg=linear+algebra，norm则表示范数，首先需要注意的是范数是对向量（或者矩阵）的度量，是一个标量（scalar）：
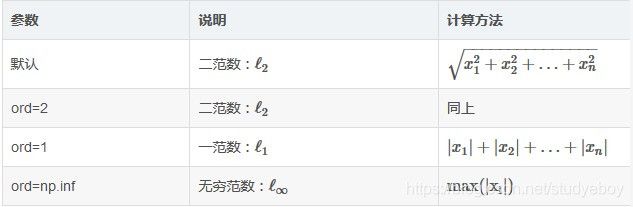
首先help(np.linalg.norm)查看其文档：

norm(x, ord=None, axis=None, keepdims=False)

ord为设置具体范数值，axis向量的计算方向，keepdims设置是否保持维度不变。

np.inner

>>> help(np.inner)
Help on built-in function inner in module numpy.core.multiarray:

inner(...)
    inner(a, b)
    
    Inner product of two arrays.
    
    Ordinary inner product of vectors for 1-D arrays (without complex
    conjugation), in higher dimensions a sum product over the last axes.
    
    Parameters
    ----------
    a, b : array_like
        If `a` and `b` are nonscalar, their last dimensions must match.
    
    Returns
    -------
    out : ndarray
        `out.shape = a.shape[:-1] + b.shape[:-1]`
    
    Raises
    ------
    ValueError
        If the last dimension of `a` and `b` has different size.
    
    See Also
    --------
    tensordot : Sum products over arbitrary axes.
    dot : Generalised matrix product, using second last dimension of `b`.
    einsum : Einstein summation convention.
    
    Notes
    -----
    For vectors (1-D arrays) it computes the ordinary inner-product::
    
        np.inner(a, b) = sum(a[:]*b[:])
    
    More generally, if `ndim(a) = r > 0` and `ndim(b) = s > 0`::
    
        np.inner(a, b) = np.tensordot(a, b, axes=(-1,-1))
    
    or explicitly::
    
        np.inner(a, b)[i0,...,ir-1,j0,...,js-1]
             = sum(a[i0,...,ir-1,:]*b[j0,...,js-1,:])
    
    In addition `a` or `b` may be scalars, in which case::
    
       np.inner(a,b) = a*b
    
    Examples
    --------
    Ordinary inner product for vectors:
    
    >>> a = np.array([1,2,3])
    >>> b = np.array([0,1,0])
    >>> np.inner(a, b)
    2
    
    A multidimensional example:
    
    >>> a = np.arange(24).reshape((2,3,4))
    >>> b = np.arange(4)
    >>> np.inner(a, b)
    array([[ 14,  38,  62],
           [ 86, 110, 134]])
    
    An example where `b` is a scalar:
    
    >>> np.inner(np.eye(2), 7)
    array([[ 7.,  0.],
           [ 0.,  7.]])

>>> a = np.arange(24).reshape((2,3,4))
>>> print(a)
[[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]]

 [[12 13 14 15]
  [16 17 18 19]
  [20 21 22 23]]]
>>> b = np.arange(4)
>>> print(b)
[0 1 2 3]
>>> print(np.inner(a,b))
[[ 14  38  62]
 [ 86 110 134]]
>>> a = np.array([1,2,3])
>>> b = np.array([0,1,0])
>>> print(np.inner(a, b))
2
>>> print(np.inner(np.eye(2), 7))
[[7. 0.]
 [0. 7.]]
>>> 

np.dot

>>> help(np.dot)
Help on built-in function dot in module numpy.core.multiarray:

dot(...)
    dot(a, b, out=None)
    
    Dot product of two arrays. Specifically,
    
    - If both `a` and `b` are 1-D arrays, it is inner product of vectors
      (without complex conjugation).
    
    - If both `a` and `b` are 2-D arrays, it is matrix multiplication,
      but using :func:`matmul` or ``a @ b`` is preferred.
    
    - If either `a` or `b` is 0-D (scalar), it is equivalent to :func:`multiply`
      and using ``numpy.multiply(a, b)`` or ``a * b`` is preferred.
    
    - If `a` is an N-D array and `b` is a 1-D array, it is a sum product over
      the last axis of `a` and `b`.
    
    - If `a` is an N-D array and `b` is an M-D array (where ``M>=2``), it is a
      sum product over the last axis of `a` and the second-to-last axis of `b`::
    
        dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])
    
    Parameters
    ----------
    a : array_like
        First argument.
    b : array_like
        Second argument.
    out : ndarray, optional
        Output argument. This must have the exact kind that would be returned
        if it was not used. In particular, it must have the right type, must be
        C-contiguous, and its dtype must be the dtype that would be returned
        for `dot(a,b)`. This is a performance feature. Therefore, if these
        conditions are not met, an exception is raised, instead of attempting
        to be flexible.
    
    Returns
    -------
    output : ndarray
        Returns the dot product of `a` and `b`.  If `a` and `b` are both
        scalars or both 1-D arrays then a scalar is returned; otherwise
        an array is returned.
        If `out` is given, then it is returned.
    
    Raises
    ------
    ValueError
        If the last dimension of `a` is not the same size as
        the second-to-last dimension of `b`.
    
    See Also
    --------
    vdot : Complex-conjugating dot product.
    tensordot : Sum products over arbitrary axes.
    einsum : Einstein summation convention.
    matmul : '@' operator as method with out parameter.
    
    Examples
    --------
    >>> np.dot(3, 4)
    12
    
    Neither argument is complex-conjugated:
    
    >>> np.dot([2j, 3j], [2j, 3j])
    (-13+0j)
    
    For 2-D arrays it is the matrix product:
    
    >>> a = [[1, 0], [0, 1]]
    >>> b = [[4, 1], [2, 2]]
    >>> np.dot(a, b)
    array([[4, 1],
           [2, 2]])
    
    >>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
    >>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
    >>> np.dot(a, b)[2,3,2,1,2,2]
    499128
    >>> sum(a[2,3,2,:] * b[1,2,:,2])
    499128

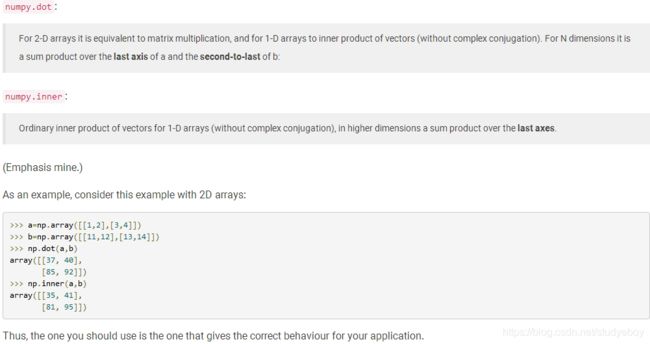
np.inner和np.dot区别

np.einsum

einsum(Einstein summation convention)函数使用爱因斯坦求和约定，在NumPy数组上指定操作。具有强大的表现力和智能循环，在速度和内存效率方面通常可以超越常见的array函数。
使用einsum的关键是为输入数组的轴和想要输出的数组选择正确的标签。例如：矩阵乘法是将行与列相乘，然后对乘积结果求和。对于两个二维数组A和B，矩阵乘法操作可以用np.einsum(‘ij,jk->ik’,A,B)完成。'ij,jk->ik’在箭头处分成两部分，左侧部分标记输入数组的轴：'ij’标记A，'jk’标记B，字符串的右侧部分用字母’ik’标记单个输出数组的轴。

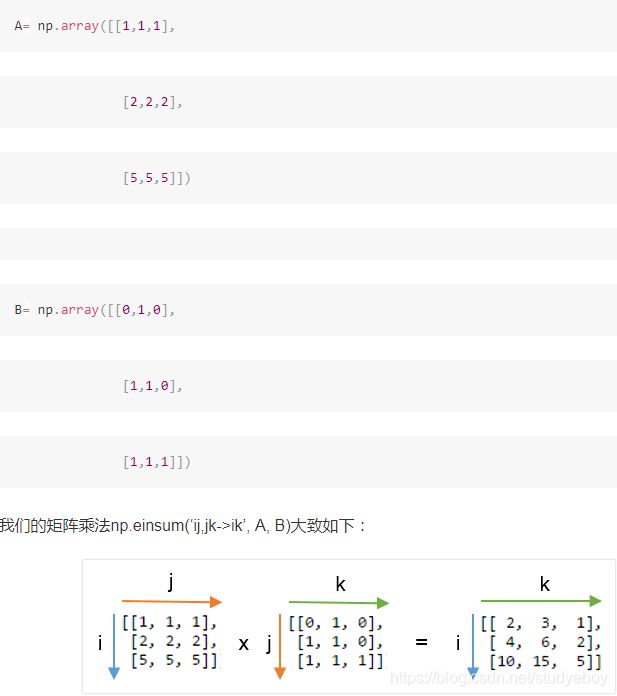
输出数组的计算方法遵循以下三原则：

• 在输入数组中重复的字母意味着值沿这些轴相乘。乘积结果为输出数组的值。
• 输出中省略的字母意味这沿该轴的值将相加。
• 可以按照喜欢的顺序返回没有进行累加的轴。
  

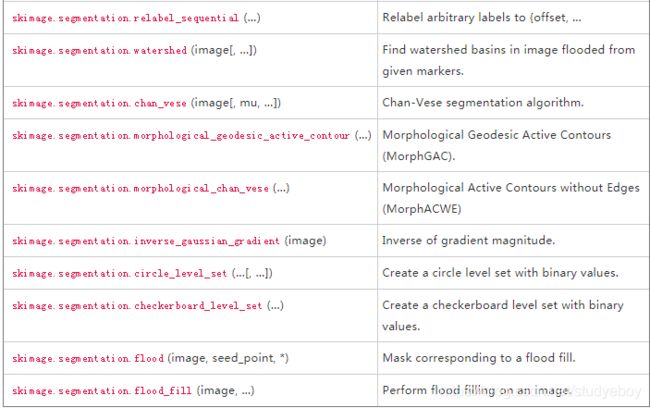
scikit-image

内建模块

deque

使用list进行数据存储时，按索引访问元素很快，因为list是线性存储，数据量大的时候，插入和删除效率很低，deque是为了高效实现插入和删除操作的双向列表，适合用于队列和栈：

from collections import deque
q = deque(['a', 'b', 'c'])
q.append('x')
q.appendLeft('y')
print(q)

#输出
deque(['y', 'a', 'b', 'c', 'x'])

PrettyTable 模块

PrettyTable是Python中的一个第三方库，用来生成美观的ASCII格式的表格。

安装

pip install prettytable

导入

from prettytable import PrettyTable

ctypes模块

ctypes是Python的一个外部库，提供和C语言兼容的数据类型，可以很方便的调用C DLL中的函数。

Python的ctypes要使用C函数，需要先将C编译成动态链接库的形式，即Windows下的.dll文件，或者Linux下的.so文件。Windows系统下的C标准库动态链接文件为msvcrt.dll。Linux系统下的C标准库动态链接文件为libc.so.6(在目录/lib/x86_64-linux-gnu下)。
导入C标准库，并使用printf函数打印一条消息。

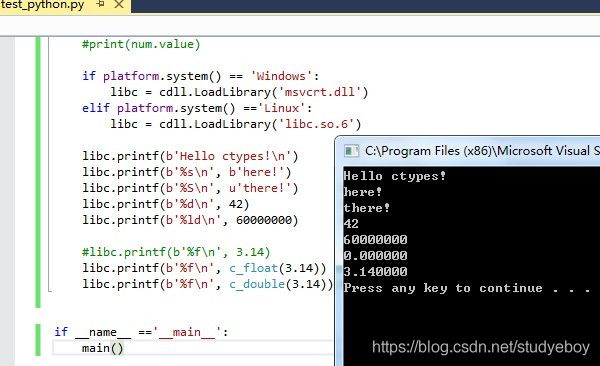
在交互窗口，不知道是什么原因还未解决：

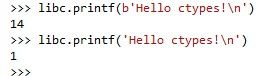
PIL

PIL即Python Imaging Library，也即我们所称的Pillow，是一个很流行的图像库，它比opencv更为轻巧，正因为如此，它深受大众的喜爱。
PIL读进来的图像是一个对象，而不是我们所熟知的numpy矩阵。

from PIL import Image
import numpy as np
img = Image.open('1.jpg')
print (img.format) # 输出：JPEG
print (img.size)  # 输出：（422,563）注意：省略了通道（w,h）
print (img.mode)  #输出： RGB  L为灰度图，RGB为真彩色，RGBA为加了透明通道
img.show()    # 显示图片

#灰度图的读取
gray = Image.open('1.jpg').convert('L')
gray.show()

#pillow 读进来的图片不是矩阵，需要将图片转为矩阵
arr = np.array(img)
print (arr.shape) #输出：（563,422,3）
print (arr.dtype) #输出：uint8

#存储图片
#矩阵再转为图像
save_img = Image.fromarray(arr)
save_img.save('2.jpg')

#图像操作
#分离合并通道
r,g,b = img.split()
new_img = Image.merge('RGB', (b,g,r))
copy_img = img.copy() #复制图像

#ROI 获取
roi = img.crop((0,0,300,300)) #(左上x，左上y，右下x，右下y)坐标
roi.show()

内置函数

isinstance()

Python 中的isinstance()函数，用来判断一个函数是否是一个已知的类型，类似type()。

isinstance(object, classifo)
#object：实例对象
#classinfo：可以是直接或者间接类名、基本类型或者由它们组成的元组。
#返回值：如果对象的类型与参数的类型(classinfo)相同则返回TRUE，否则返回False

问题

'\u’错误

解决方法 在出现’\u’的代码处将’\u’转换为’\u’

SyntaxError: (unicode error) 'unicodeescape' codec can't decode bytes in position 726-727: truncated \uXXXX escape
#解决方法在出现'\u'的代码处将'\u'转换为'\\u'

参考文献

1. https://www.cnblogs.com/hongten/p/hongten_python_glob.html
2. https://www.yiibai.com/scipy/scipy_ndimage.html?app=post
3. https://docs.scipy.org/doc/numpy/reference/generated/numpy.flip.html
4. https://www.cnblogs.com/touch-skyer/p/8509217.html
5. https://blog.csdn.net/lanchunhui/article/details/52700895
6. https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.strides.html
7. https://blog.csdn.net/shwan_ma/article/details/78244044
8. https://blog.csdn.net/tymatlab/article/details/79009618
9. https://blog.csdn.net/mosesRen/article/details/80275039
10. https://blog.csdn.net/u010359398/article/details/82766474
11. numpy.stack最通俗的理解
12. 图解Numpy的tile函数
13. 稀疏矩阵（coo_matrix, csr_matrix, csc_matrix）的定义和存取
14. scipy csr_matrix和csc_matrix函数详解
15. python 库 Numpy 中如何求取向量范数 np.linalg.norm(求范数)（向量的第二范数为传统意义上的向量长度），（如何求取向量的单位向量）
16. 使用 ctypes 进行 Python 和 C 的混合编程
17. Python各类图像库的图片读写方式总结
18. Python中的isinstance()函数
19. difference between numpy dot() and inner()
20. NumPy中einsum的基本介绍
21. Scipy：高级科学计算
22. scikit-image
23. collections