sigmoid_cross_entropy_with_logits函数笔记

@ TOC

tf.nn.sigmoid_cross_entropy_with_logits()介绍

线性模型假设

• 样本 $(x,z)$, 其中X是样本的点，$z$是样本的标签，假设我们的线性模型如下

$$y=\omega \ast x+b$$

这个函数用到的基础函数

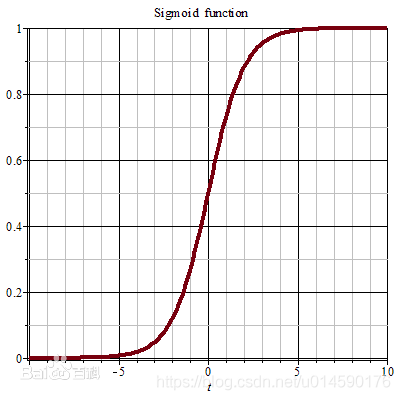
sigmoid 函数

其实logistic函数也就是经常说的sigmoid函数，它的几何形状也就是一条sigmoid曲线（S型曲线）。

$$f(x)=\frac{1}{1+e^{-x}}$$

logistic和sigmoid函数的区别是，logistics是二分类问题而sigmoid是解决多分类问题的函数。

交叉熵

假设x是正确的概率分布，而y是我们预测出来的概率分布，这个公式算出来的结果，表示y与正确答案x之间的错误程度（即：y错得有多离谱），结果值越小，表示y越准确，与x越接近。

$$h(x,y)=-\sum _{i=1}^n{x}_i\ast ln(y_i)$$

下面举个交叉熵的例子：

比如：

x的概率分布为：{1/4 ，1/4，1/4，1/4}，现在我们通过机器学习，预测出来二组值：

y1的概率分布为 {1/4 , 1/2 , 1/8 , 1/8}

y2的概率分布为 {1/4 , 1/4 , 1/8 , 3/8}

从直觉上看，y2分布中，前2项都100%预测对了，而y1只有第1项100%对，所以y2感觉更准确，看看公式算下来，是不是符合直觉：

$$\begin{gathered} H(x,y_1)=-\sum _{i=1}^n{x}_i\ast ln(y_{1i})=\frac{9}{4} \\ H(x,y_1)=-\sum _{i=1}^n{x}_i\ast ln(y_{2i})=\frac{9}{4}=\frac{10-ln(3)}{4} \\ <\frac{10-1}{4}=H(x,y_1) \end{gathered}$$

对比结果，$H(x,y_1)$算出来的值为$\frac{9}{4}$，而$H(x,y_2)$的值略小于$\frac{9}{4}$，根据刚才的解释，交叉熵越小，表示这二个分布越接近，所以机器学习中，经常拿交叉熵来做为损失函数(loss function)。

---

损失函数loss

假设$z$为模型的样本标签，而$y$是训练后的模型对应的值，我们求模型的表现，用样本标签和模型结果进行运算，求损失函数$Loss$：

$$\begin{gathered} Loss(y,z)=\frac{1}{2}(y-z{)}^2 \\ =\frac{1}{2}((\omega \ast x+b)-z{)}^2 \end{gathered}$$

如果直接用sigmoid 函数后，我们的$Loss$函数将有可能是一个非凸函数(出现多个局部最优点,可能对后面的权值和偏差参数调整不利)，可能效果图就是下面这样的(纵轴是loss,横轴是训练的回合数)：

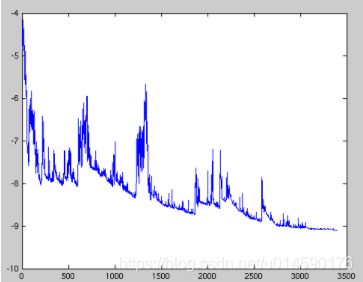
会导致我们的随机梯度下降(SGD, Stochastic Gradient Descent )陷入局部最小的陷阱中。如上图，SGD 因为更新比较频繁，会造成 cost function 有严重的震荡。

如果此时进行梯度的参数更新的话，就会这样

• 梯度更新迭代的调参

$$\begin{gathered} {\omega }_i={\omega }_{i-1}-\eta \ast {▽}_{\omega }J(y,z) \\ ={\omega }_{i-1}-\eta \ast {▽}_{\omega }\frac{1}{2}(y-z{)}^2 \\ ={\omega }_{i-1}-\eta \ast {▽}_{\omega }\frac{1}{2}((\omega \ast x+b)-z{)}^2 \end{gathered}$$

每个回合都会更新$\omega$, $b$的值，从而更新$y=\omega \ast x+b$ 的函数模型。

• 为了获得一个凸性的损失函数（就创造了这样一个性质良好的函数（PS:还可导哦））引进交叉熵函数。

For brevity, let x = logits, z = labels. The logistic loss is

$$\begin{gathered} z\ast -log(sigmoid(x))+(1-z)\ast -log(1-sigmoid(x)) \\ =z\ast -log(1/(1+exp(-x)))+(1-z)\ast -log(exp(-x)/(1+exp(-x))) \\ =z\ast log(1+exp(-x))+(1-z)\ast (-log(exp(-x))+log(1+exp(-x))) \\ =z\ast log(1+exp(-x))+(1-z)\ast (x+log(1+exp(-x)) \\ =(1-z)\ast x+log(1+exp(-x)) \\ =x-x\ast z+log(1+exp(-x)) \end{gathered}$$

注意和交叉熵的区别

---

参考文章：

交叉熵：https://www.cnblogs.com/yjmyzz/p/7822990.html
为何sigmoid激活函数要配合sigmoid_cross_entropy_with_logits损失函数使用？：https://blog.csdn.net/u014590176/article/details/90381413