简单线性回归分析【笔记】

简单线性回归分析

目录

1. 摘要 / 引言

回归分析是统计学的核心，是一个广义概念，通常指用一个或多个自变量（也成解释变量、预测变量）来预测应变量（也称因变量、校变量或结果变量）。简单线性回归只包括一个应变量和一个自变量。这种回归也称一元线性回归

2. 算法名称

简单线性回归，一元线性回归描述

3. 归类

回归分析是处理自变量和应变量之间关系的一种统计方法和技术。

4. Metaphor

简单回归是描述自变量和应变量之间的线性关系。其几何意义是用一条直线来近似表示因变量和自变量的关系。而直线上某一点 (x,y^) 对应的 y^ ，为自变量 Y 在 x 最有可能出现的值。如图1

图1

5. Strategy

简单线性回归模型为(1)式

yi=β0+β1xi+εi        (1)

误差项 εi 是一个随机变量，该误差是 y 中不能被线性模型解释的变异。回归模型服从以下假设[1]
1. 解析变量 x 是非随机变量；
2. εi∼N(0,σ2) ，且彼此独立。
由模型可知， y 的期望随着 x 变化而变化，用回归方程（2）描述这种变化关系

E(yi)=β0+β1xi         (2)

因为 εi∼N(0,σ2) ，因此 yi∼N(β0+β1xi,σ2)        

6. Procedure

简单线性回归分析可分为以下步骤：
1. 针对问题，确定因变量和自变量
2. 收集数据
3. 画散点图，并观察确定因变量和自变量的关系
4. 设计理论模型
5. 参数估计：可以通过最小二乘法或最大似然估计可以估计参数 β0 和 β1
6. 模型检验：模型检验包括拟合度度量、显著性检验、残差分析
7. 预测分析

本文仅讨论一元线性回归，因此对步骤1~4不展开讨论

6.1 参数估计

常用的估计方法有最小二乘法（OLSE）和最大似然法。本文介绍基于最小二乘法的参数估计。
最小二乘法的思想：最小化 n 个样本的观测值 yi 和回归值 yi^ 离差平方和

最小二乘法准则

Q(β0^ β1^)=minβ0,β1(yi−yi^)2          （3）

对 Q(β0^，β1^) 求偏导数，并令求导公式为0，如下

⎧⎩⎨⎪⎪⎪⎪⎪⎪∣∣∣∂Q∂β0∣∣∣=2∑(yi−β0^−β1xi^)=0∣∣∣∂Q∂β1=∣∣∣2∑(yi−β0^−β1xi^)xi=0          （4）

通过公式（4）可估计出参数

---

6.2 模型检验

模型检验一般包括显著性检验、拟合度度量、残差分析

6.2.1 回归系数的显著性检验

回归系数显著性检验是检验自变量 x 对因变量 y 的影响是否显著。常用的检验方法有t检验、F检验、相关系数检验。在一元线性回归中，t检验、F检验、相关系数检验是等价的。但是在多元线性回归中，三者的意义就不一样了

检验的原假设:

H0:β1=0

备择假设：

H1:β1≠0

t检验

由于 β1^∼N(β1,σ2∑(xi−x¯)2) (参考文献【1】P29)
所以 β1^sβ1^ 是一个自由度为 n−2 的 t 分布。
其中 β1^ 的标准差 sβ1^=σ2∑(xi−x¯)2−−−−−−−−√
σ2 的无偏估计 σ2^=1n−2∑(yi−yi^)2

F检验

在一元线性回归中，F检验也可用于回归系数显著性检验。但在多元线性回归中，F检验只能检验回归方程总体的显著关系

检验统计量：

F=MSRMSE

其中 MSR=SSR回归自由度(即自变量个数) ，回归平方和 SSR=∑(yi^−yi¯)2

MSE=SSEn−2 ，残差平方和和 SSE=∑(yi^−yi)2

相关系数

相关系数的直观意义如下

6.2.2 拟合度度量

判定系数（样本决定系数） r2 是度量回归方程与样本观测值的拟合优度，反映了自变量的变异对因变量的变异的解析程度。

r2=SSRSSE≤1

当 r2 接近1，说明因变量变化大部分能由线性方程解释

6.2.3 残差分析

残差定义： ei=yi−yi^=yi−β0^−β1^xi
注意和误差项的区别（误差项： εi=β0−β1xi ）
残差 ei 可以看作是误差 εi 的估计值
残差分析既可用于证实模型的有效性（即误差 ε 是否满足假设），也可用于检验异常值

残差的相关性质和概念

1. E(ei)=0
2. var(ei)=(1−hi)σ2 其中 hi=1n+(xi−x¯)2∑(xi−x¯)2 称为杠杆率。该性质说明远离 x¯ 时，相应 ei 的方差会变小，也就是残差存在方差不等的问题
3. ∑ei=0 ， ∑xiei=0

标准化残差： ZREi=eiσ^
学生化残差： SREi=eiσ1−hi√^ ，其中 hi 为杠杆率。学生化残差进一步解决了残差的方差不等问题

实模型的有效性分析

残差图：残差图有关于x的残差图，和关于y的残差图。对于一元线性回归，两种残差图都可用于分析，而y的残差图还能应用到多元线性回归上

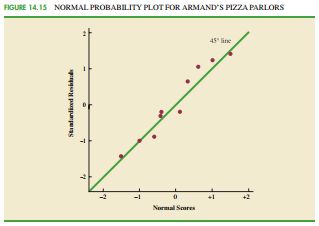
正太概率图：详细说明参考文献【2】Page：329-330。这里只说结论。如图，当较多的点聚集在正太概率图的45度线上，说明误差和项 ε 服从正太分布

异常值检验

一般认为 SREi>3 的观察值为异常

有影响的观测值

有影响的观测值就是删除该值后，回归方程的估计会发生较大变化。有影响的观测值一般由大的残差和高杠杆率交互作用产生。注意，有影响的观测值不一定是异常值
度量指标：库克D统计量

6.3 预测分析

区间预测

1.因变量新值的区间预测：详细推导参考【1】。估计 y0 的置信概率为 1−α 的置信区间为

y0^±tα/21+h0−−−−−√σ^

可以发现，靠近 x¯ 附近的预测精度最高

2.因变量新值的平均值的区间预测：置信概率为 1−α 的置信区间为

y0^±tα/2h0−−√σ^

7. Summarize Parameters

具体介绍算法参数的变化范围、参数变化对算法性能的影响，以及一些常用的配置方案

1. 相关系数：相关系数 r 的符号与自变量系数的符号相同。相关系数有个明显确定。样本数 n 越少 |r| 越接近1，当 n 越大 |r| 容易偏小
2. 由于 β1^∼N(β1,σ2∑(xi−x¯)2) ，说明 x 越分散， β1^ 的估计越准确
3. 判定系数（样本决定系数） r2 在不通的实际问题中，其判断阈值存在很大差异。在社会学科中，0.25是令人满意的。而在自然科学，0.6比较常见。【2】p312
4. 回归分析适用于内推，不适用与外推

References

[1]. 应用回归分析 何晓群
[2]. 商务与经济统计 张建化等