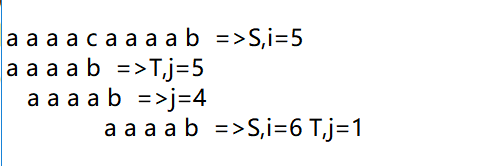据结构(五)-- 模式匹配及KMP算法(python)
《数据结构C语言版》P79-84
---------------------------------------------------
1、简单的模式匹配
算法思想
主串S,S[0]存放串S的长度;模式串T,T[0]存放串T的长度。
设置两重循环,i指向主串S的索引,j'指向模式串T的索引。从主串的i=pos开始,尝试匹配模式串T,如果S[i]==T[j],则主串S和模式串T同时后移一个,继续匹配;如果S[i]!=T[j],则回溯到主串的i=i-j+2的位置,也就是外层循环的下一个位置,重新开始匹配模式串。
时间复杂度为O(n*m)python3
def index(S, T, pos): # S为主串,T为模式串,pos为查找主串的起始位置
i, j = pos, 1
while i <= S[0] and j <= T[0]:
if S[i] == T[j]:
i += 1
j += 1
else:
i = i - j + 2
j = 1
if j > T[0]:
return i - T[0]
else:
return 0 # 不存在这样的子串
if __name__ == '__main__':
S = list('abbaba')
S.insert(0, len(S)) # S = [6, 'a', 'b', 'b', 'a', 'b', 'a']
T = list('aba')
T.insert(0, len(T)) # T = [3, 'a', 'b', 'a']
print(index(S, T, 1))----------------------------------------------------------------------------------------------------------------------------------------------------------------------
2、KMP算法
算法思想
不需要回溯i,而是利用已经得到的部分匹配的结果将模式向右滑动尽可能远的一段距离后,继续进行比较。
在比较主串S和模式串T的某一位S[i]和T[j]不匹配时,不需移动i,而移动模式串的j,找到模式串的另一位j和S[i]进行比较。另一位j依靠模式串的next函数值确定。
next函数计算,下图解释了为什么模式串可以直接移动到next[j]处和S[i]比较。next函数是对应位的前缀+1。下图中的不同指的是S中i和T中的j不同时的T中的j的位置。详细解释见数P82-83。
python3计算next函数
def getNext(T):
next1 = [T[0], 0]
i, j = 1, 0
while i < T[0]:
if j == 0 or T[i] == T[j]: # 初始化next[1]以及找不到任何的Pk'==Pj时next[j+1]=1和计算Pk==Pj时,next[j+1] = next[j] + 1
i += 1
j += 1
next1.append(j)
else:
j = next1[j]
return next1----------------------------------------------------------------------------------------------------------------------------------------------------------------------
nextval函数优化,有些情况为:当前S中的i和T中的j不匹配,于是寻找next[j]再次和S中的i匹配,但是如果next[j]代表的字符和原本的j代表的字符相同,此次匹配就是无效的,因为j已经和S中i比较过,不需要再次比较。如图。会重复比较S[5]和T[5]、T[4]、T[3]、T[3]、T[2]、T[1]
优化后为:
计算优化的next函数
def getNextVal(T):
nextval = [T[0], 0]
i, j = 1, 0
while j < T[0]:
if j == 0 or T[i] == T[j]:
i += 1
j += 1
if T[i] != T[j]:
nextval.append(j)
else:
nextval.append(nextval[j])
else:
j = nextval[j]
return nextval----------------------------------------------------------------------------------------------------------------------------------------------------------------------
KMP完整算法
def index_KMP(S, T, pos):
NextVal = getNext(T)
i, j = pos, 1
while i <= S[0] and j <= T[0]:
if j == 0 or S[i] == T[j]: # j==0表示主串当前的S[i]和模式串的T[1]都不匹配,只有将主串和模式串同时后移一位继续匹配;
# S[i] == T[j]表示当前主串和模式串指向的字符匹配,继续后移查看下一位是否匹配
i += 1
j += 1
else:
j = NextVal[j] # 移动T用T的另一个字符和S匹配
if j > T[0]:
return i - T[0]
else:
return 0
def getNext(T):
next1 = [T[0], 0]
i, j = 1, 0
while i < T[0]:
if j == 0 or T[i] == T[j]: # 初始化next[1]以及找不到任何的Pk'==Pj时next[j+1]=1和计算Pk==Pj时,next[j+1] = next[j] + 1
i += 1
j += 1
next1.append(j)
else:
j = next1[j]
return next1
def getNextVal(T):
nextval = [T[0], 0]
i, j = 1, 0
while j < T[0]:
if j == 0 or T[i] == T[j]:
i += 1
j += 1
if T[i] != T[j]:
nextval.append(j)
else:
nextval.append(nextval[j])
else:
j = nextval[j]
return nextval
if __name__ == '__main__':
S = list('acabaabaabcacaabc')
S.insert(0, len(S)) # S = [6, 'a', 'b', 'b', 'a', 'b', 'a']
T = list('abaabc')
T.insert(0, len(T)) # T = [3, 'a', 'b', 'a']
getNext(T)
T1 = list('aaaab')
T1.insert(0, len(T1))
getNextVal(T1)
print(index_KMP(S, T, 1))