java8 Arrays.sort 与Arrays.parallelSort

java8 Arrays.sort 与Arrays.parallelSort

Sort方法

java8中Arrays.sort()方法有很多重载方式，先来看看对byte类型的排序

static void sort(byte[] a, int left, int right) {
    // Use counting sort on large arrays
    if (right - left > COUNTING_SORT_THRESHOLD_FOR_BYTE) {
        int[] count = new int[NUM_BYTE_VALUES];

        for (int i = left - 1; ++i <= right;
            count[a[i] - Byte.MIN_VALUE]++
        );
        for (int i = NUM_BYTE_VALUES, k = right + 1; k > left; ) {
            while (count[--i] == 0);
            byte value = (byte) (i + Byte.MIN_VALUE);
            int s = count[i];

            do {
                a[--k] = value;
            } while (--s > 0);
        }
    } else { // Use insertion sort on small arrays
        for (int i = left, j = i; i < right; j = ++i) {
            byte ai = a[i + 1];
            while (ai < a[j]) {
                a[j + 1] = a[j];
                if (j-- == left) {
                    break;
                }
            }
            a[j + 1] = ai;
        }
    }
}

如果大于域值那么就使用计数排序法，否则就使用插入排序。具体排序算法分析在下面给出。

再来看看其他类型（float，double）的数组的排序。代码如下：

static void sort(float[] a, int left, int right,
                 float[] work, int workBase, int workLen) {

    while (left <= right && Float.isNaN(a[right])) {
        --right;
    }
    for (int k = right; --k >= left; ) {
        float ak = a[k];
        if (ak != ak) { // a[k] is NaN
            a[k] = a[right];
            a[right] = ak;
            --right;
        }
    }

    doSort(a, left, right, work, workBase, workLen);

    int hi = right;

    while (left < hi) {
        int middle = (left + hi) >>> 1;
        float middleValue = a[middle];

        if (middleValue < 0.0f) {
            left = middle + 1;
        } else {
            hi = middle;
        }
    }
    while (left <= right && Float.floatToRawIntBits(a[left]) < 0) {
        ++left;
    }
    for (int k = left, p = left - 1; ++k <= right; ) {
        float ak = a[k];
        if (ak != 0.0f) {
            break;
        }
        if (Float.floatToRawIntBits(ak) < 0) { // ak is -0.0f
            a[k] = 0.0f;
            a[++p] = -0.0f;
        }
    }
}

首先，将数组中的NaN全部排到最后，然后调用dosort方法进行排序。然后在针对-0.0f和0.0f进行处理。
doSort()方法由于代码过多，这里不再贴上了。主要还是用到了插入排序，不过该方法后面讲数组分为很多份，然后递归的调用。

parallelSort

parallelSort是java8中新出的一种排序API，这是一种并行排序，Arrays.parallelSort使用了Java7的Fork/Join框架使排序任务可以在线程池中的多个线程中进行，Fork/Join实现了一种任务窃取算法，一个闲置的线程可以窃取其他线程的闲置任务进行处理。代码如下：

public static void parallelSort(int[] a, int fromIndex, int toIndex) {
    rangeCheck(a.length, fromIndex, toIndex);
    int n = toIndex - fromIndex, p, g;
    if (n <= MIN_ARRAY_SORT_GRAN ||
        (p = ForkJoinPool.getCommonPoolParallelism()) == 1)
        DualPivotQuicksort.sort(a, fromIndex, toIndex - 1, null, 0, 0);
    else
        new ArraysParallelSortHelpers.FJInt.Sorter
            (null, a, new int[n], fromIndex, n, 0,
             ((g = n / (p << 2)) <= MIN_ARRAY_SORT_GRAN) ?
             MIN_ARRAY_SORT_GRAN : g).invoke();
}

这个方法使用了一个临界值，如果是小容量的数组或者分块为1，其实和普通的sort方法一样。否则就用的是Fork/Join。

性能对比

下面进行这两种sort方法的性能对比：
使用的测试代码如下：

public class TestSort {

  final int UPPER_LIMIT = 0xffffff;
  final int ROUNDS = 10;
  final int INCREMENT = 5;
  final int INIT_SIZE = 1000;

  public static void main(String[] args){
    new TestSort().test();
  }

  public void test() {
    // 测试数组大小从INIT_SIZE开始,每次增加INCREMENT倍,直到超过UPPER_LIMIT.
    for (int capacity = INIT_SIZE; capacity <= UPPER_LIMIT; capacity *= INCREMENT) {
      ArrayList list = new ArrayList(capacity);

      for (int i = 0; i < capacity; i++) {
        list.add((int) (Math.random() * capacity));
      }
      // avgTimeOfParallelSort:parallelSort经过ROUNDS次排序所耗费的平均时间
      double avgTimeOfParallelSort = 0;
      // avgTimeOfSort:sort经过ROUNDS次排序所耗费的平均时间
      double avgTimeOfSort = 0;

      for (int i = 1; i <= ROUNDS; i++) {
        // 每次排序都先打乱顺序
        Collections.shuffle(list);

        Integer[] arr1 = list.toArray(new Integer[capacity]);
        Integer[] arr2 = arr1.clone();

        avgTimeOfParallelSort += counter(arr1, true);
        avgTimeOfSort += counter(arr2, false);

      }

      output(capacity, avgTimeOfParallelSort / ROUNDS, avgTimeOfSort
              / ROUNDS);
    }
  }

  /**
   * 用于计算排序花费的时间
   *
   * @param arr
   *            要排序的数组
   * @param useParallelSort
   *            true:使用parallelSort;false:使用sort
   * @return 返回花费的时间
   */
  private double counter(Integer[] arr, boolean useParallelSort) {
    long begin, end;
    begin = System.nanoTime();
    if (useParallelSort) {
      Arrays.parallelSort(arr);
    } else {
      Arrays.sort(arr);
    }
    end = System.nanoTime();
    return BigDecimal.valueOf(end - begin, 9).doubleValue();

  }

  /**
   *
   * @param capacity
   *            当前数组容量
   * @param avgTimeOfParallelSort
   *            parallelSort花费的平均时间
   * @param avgTimeOfSort
   *            sort花费的平均时间
   */
  private void output(int capacity, double avgTimeOfParallelSort,
                      double avgTimeOfSort) {
    System.out
            .println("==================================================");
    System.out.println("Capacity:" + capacity);
    System.out.println("ParallelSort:" + avgTimeOfParallelSort);
    System.out.println("Sort:" + avgTimeOfSort);
    System.out.println("Winner is:"
            + (avgTimeOfParallelSort < avgTimeOfSort ? "ParallelSort"
            : "Sort"));
    System.out
            .println("==================================================");
  }

}

测试结果为：

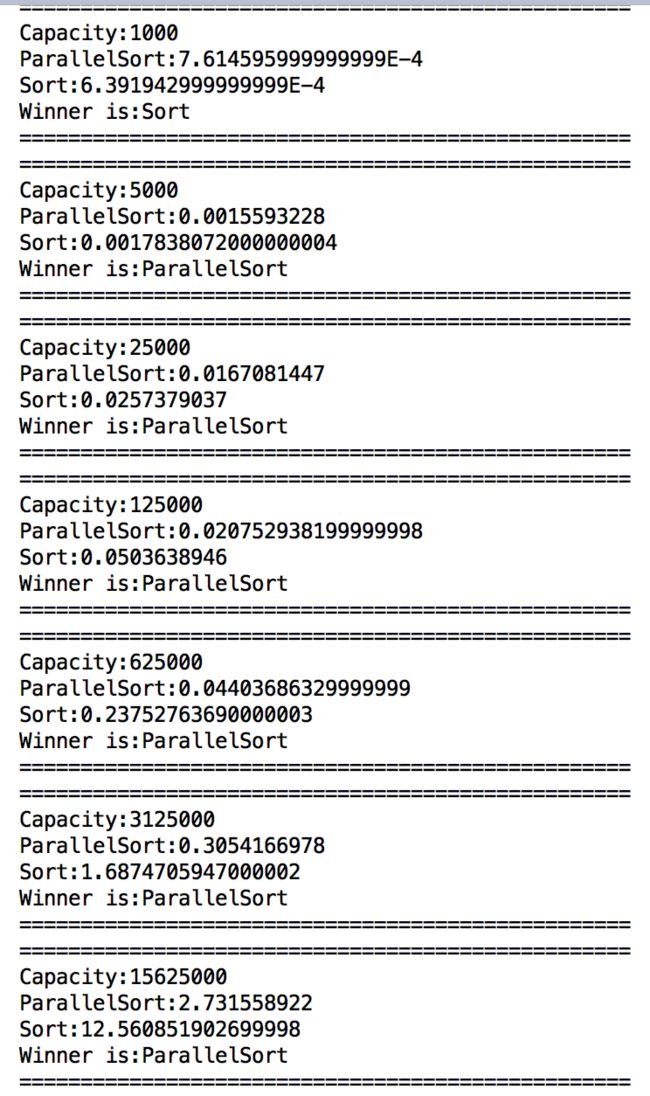
发现数据量越大，parallelSort的优势就越明显。

常用排序算法

发现jdk源码中写的排序算法都很精简，值得学习，这里讲所看到的算法总结出来：

1.counting sort（计数排序）

计数排序是在对byte类型的数组排序的时候使用到的。主要是首先用一个临时数组保存一个元素出现的次数，数组的下标是该元素的值，然后遍历的时候就从临时数组的最大下标开始，将值赋给排序的数组，如果出现次数大于1，那么循环赋值。jdk中实现很精简，模仿写的代码如下:

public static void main(String[] args){
  int[] a = new int[]{2,1,4,5,3,2,6};
  int[] count = new int[10];

  for (int i = -1; ++i < a.length; count[a[i]]++) ;
  for (int i = 10, k = a.length; k > 0; ) {
    while (count[--i] == 0);
    int value = i;
    int s = count[i];

    do {
      a[--k] = value;
    }while (--s > 0);
  }
}

计数排序的时间复杂度为O(N),如果有用于统计次数的需求还是可以使用的。

2.insertion sort（插入排序）

插入排序的时间复杂度为0(N^2)，主要思想还是说用一个变量来保存插入值，然后依次替换。

public static void main(String[] args){
  int[] a = new int[]{2,1,4,5,3,2,6};

  for (int i = 0, j = i; i < a.length - 1; j = ++i) {
    int ai = a[i + 1];
    while (ai < a[j]) {
      a[j + 1] = a[j];
      if(j-- == 0)
        break;
    }
    a[j + 1] = ai;
  }
}

3.merge sort（归并排序）

归并排序是分治算法的一个典型例子，就是把一个数组分为大小相近的的子数组，然后把子数组排序好后通过归(Merge)手法合成一个大的排序好的数组。其实在对子数组进行排序的时候，就是用到插入排序。

public static void mergeSort(int[] src, int left, int right) {
  int length = right - left;
  if (length < INSERTIONSORT_THRESHOLD)
    insertSort(src);
  int mid = (left + right) >>> 1;
  mergeSort(src, left, mid);
  mergeSort(src, mid, right);

  if (((Comparable) src[mid - 1]).compareTo(src[mid]) <= 0) {
    System.arraycopy(src, left, src, left, length);
    return;
  }

  int[] dest = new int[length];
  for (int i = 0,p = left, q = mid; i < right; i++) {
    if(p < mid && ((Comparable)src[p]).compareTo(src[q]) <= 0)
      dest[i] = src[p++];
    else
      dest[i] = src[q++];
  }
  src = dest;
}

 归并排序的时间复杂度为O(NLogN)，不过需要额外的空间来存储数据。

4.快速排序

快速排序和归并排序都使用分治的思想来设计算法，区别在于归并排序把数组分为两个基本等长的子数组，分别排好序后再进行归并操作，而快速排序则是选取一个基准元素，拆分之后基准元素左边的元素都比基准元素小，右边的元素都不小于基准元素，这样只需要分别对两个子数组排序即可，而没有了归并操作。快排的重点在于选选取基准元素。

private static void swap(int arr[], int i, int j) {
  int tmp;

  tmp = arr[i];
  arr[i] = arr[j];
  arr[j] = tmp;
}

public static void quickSort(int arr[], int left, int right) {
  int i, last;

  if (left > right)
    return;

  swap(arr, left, (left + right) >>> 1);
  last = left;
  for (i = left + 1; i <= right; i++) {
    if (arr[i] < arr[left])
      ++last;
  }
  swap(arr, left, last);
  quickSort(arr, left, last - 1);
  quickSort(arr, last + 1, right);
}

注：性能对比代码是在网上看到一个大牛写的。但是写这篇播客的时候，发现找不到链接了。如果有人知道原文，请评论，我加上，谢谢。