详解BM算法以及其改进KMP算法原理与在python中的实现

在介绍KMP算法之前，我们先来了解另外一种算法，BM算法。

其实不论是KMP算法，还是BM算法都是字符串的模式匹配算法，那么
什么是模式匹配呢？

在严老师的书里是这样定义的：子串的定位操作通常被称为串的模式匹配。

其实就是给定两个字符串，一个被当成主串，然后在主串中寻找另一个字符串的过程。而这个过程也被称为串的模式匹配。同时我们要寻找的这个字符串被称为子串或者模式串。

pattern_str = 'ababcabcacbab'

match_str = 'abcac'

# 我在pattern_str中寻找match_str的过程，就被称为串的模式匹配

下面我们先来介绍BM算法，因为KMP算法其实是BM算法的一个改进，这个改进算法呢，是D.E.Knuth 与 V.R.Partt 还有 J.H.Morris同时发现的，也被称为克努特—莫里斯—普拉斯操作。它的简称自然就是KMP

既然我们要在主串中寻找字串所在的位置，首先应该想到的我直接用一个循环，然后看看主串是不是和模式串的第一个相等，如果相等，我就移动到主串和模式串到下一个位置，如果不相等，那么我就主串从当前循环开始的位置往后面移动一位，然后重新和模式串的第一个位置的字符进行比较。

我们假设当前 i 代表的是主串的位置，j代表的是模式串的位置

就拿上面的例子说吧，首先是i=0,j=0的时候

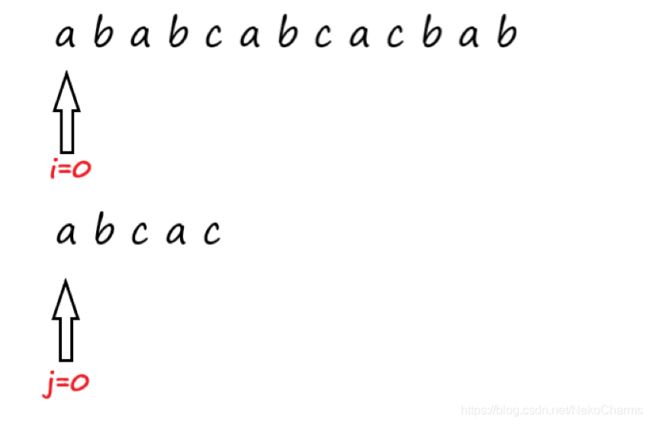
主串与模式串相等，那么我们执行i+=1,j+=1;现在i=1,j=1,主串和模式串同时移动到第二个位置 ，这时候我们发现 主串和模式串还是相等 ，那么我们再执行
i+=1,j+=1，现在来到了主串和模式串的第三个位置：

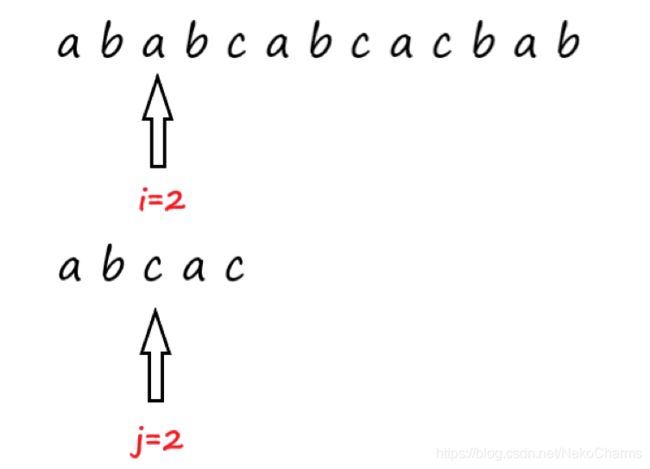
发现不相等了，那么我们只能返回模式串的开头位置,即令j=0，主串应该从最初开始的位置后移一位即 i 应该等于1

主串最先是从第一位开始和模式串匹配,在第三个位置发生失配，那么下一次应该主串从最初开始的位置往后移动一位（即第二个位置）再来和模式串的第一个位置进行匹配。

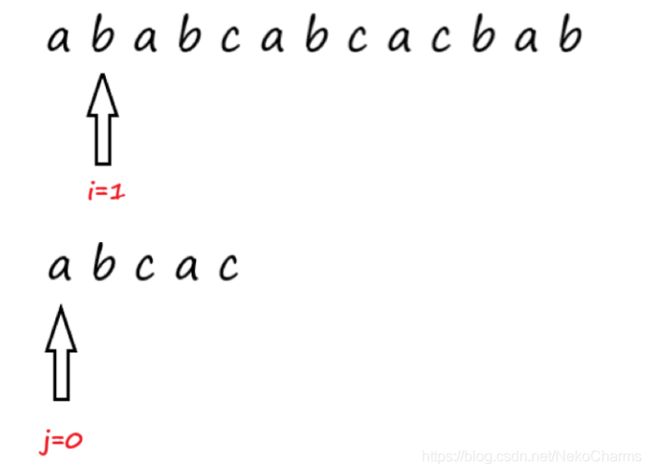
然后接着下一次的匹配，直到 i 达到了主串的末尾或者 j 到达了模式串的末尾 我们就跳出循环。

def matching(t, s):  # t是主串，s是模式串
    i = 0
    j = 0
    length_t = len(t)
    length_s = len(s)
    while i < length_t and j < length_s:  # 判断循环跳出条件
        if t[i] == s[j]:
            i += 1
            j += 1
        else:
            i = i - j + 1  # 因为如果发生失配，i应该回到当次循环开始的位置再后移一位
            j = 0          # 因为发生失配的时候，前面有j个都成功匹配了，所以说i要回到当次循环开始位置再后移一位
    if j == length_s:  # 当跳出循环的时候，如果能成功匹配的话j应该是走到了模式串的末尾然后执行j+1 刚好会等于模式串的长度
        return i-length_s
    else:
        return 'match failed'


if __name__ == '__main__':
    pattern_str = 'ababcabcacbab'
    match_str = 'abcac'
    print(matching(t=pattern_str, s=match_str))

下面是运行结果，代表模式串在主串的第五个位置开始。

这就是BM算法，但是该算法效率很低，如果主串为 ’0000000000000000001‘ 而模式串等于’00001’，每次匹配到模式串的最后一个都发生失配，每次都要让j重新回到模式串开始位置，i要回到当前i-4+1=i-3的位置。在这种最坏情况下时间复杂度为O(n*m) 其中n和m分别为模式串和子串的长度

那么有没有一种办法不让每次 j 都要回到最开始的位置 ，i 也不用每次都要回到当次循环开始的位置+1呢

下面就谈到了KMP算法，是BM算法的一种改进

首先我们来举个例子：
我们假设有这么两个字符串，主串为’aacaababccab’ ，模式串为’aababc’
按照BM算法的方法：首先 i=0,j=0,从开头判断，相等，我们全部后移一位变成 i=1,j=1，再进行匹配，相等全部后移一位 i=2,j=2，发生失配，j回到0，i回到1。

这时候会发现，其实发生失配j回到0，i回到1 ，进行匹配。这次匹配是不是应该是多余的。

我们简单分析一下，前两次没有发生失配，那么我就能知道我模式串第一个和第二个分别和主串的第一个第二个相等。再看我的模式串， 模式串第一位和第二位相等，那么是不是我能推导出来我模式串第一个和主串第二个也是相等的。


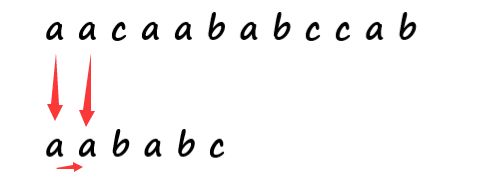
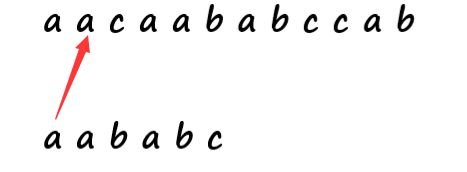
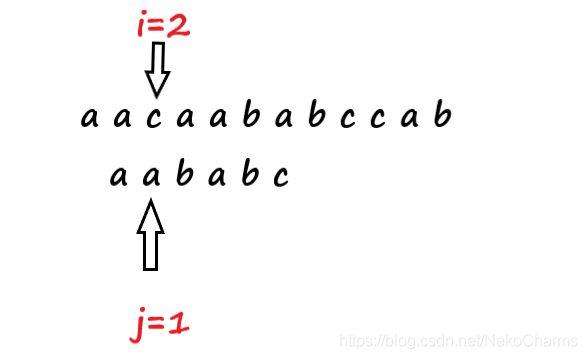
那么我还有有必要回到j=0，i=1，继续比较主串第二个和模式串第一个吗？
我就只需要令 i 不动 保持 i=2，然后把 j 回到 第二个位置上即令j=1，然后开始下一次匹配

现在我们假设当发生失配的时候，j不用每次回到开头，我们假设一个位置 k ，让如果模式串在j的位置发生失配的时候，j回到k，而不是回到开头0

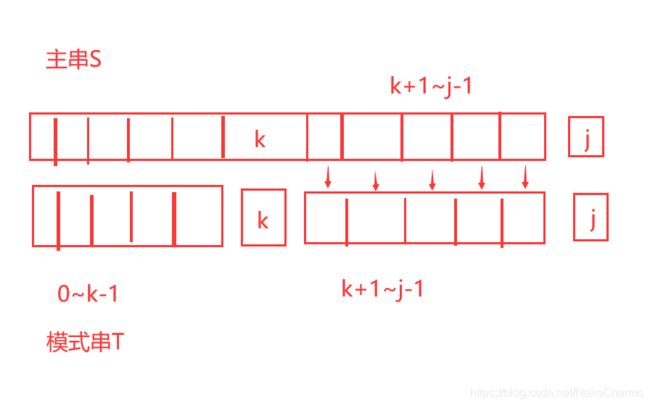
如图，既然在j个位置发生失配，那么主串和模式串从0~j-1都是相当的 ，图中箭头指出来了
模式串Tk+1 ~ Tj-1 和 主串Sk+1 ~ Sj-1相等，那么如果我们能在模式串T发现在第K个位置的前面即是从0~k-1 与k的后面从k+1~j-1如果相等。

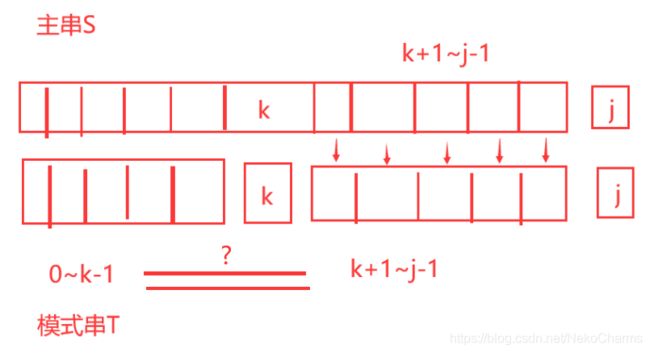
那么是不是可以的到模式串T0~k-1 与 主串Sk+1~j-1相等，那么我就没有必要再去比较这两部分了，我在i不动的前提下，令 j = k 就避免了重复的比较。

这里我们假设已经实现一个功能，k = next[j] ，当第j个位置发生失配的时候，我只需要令 j = next[j] 就可以了

那么自然可以写出相应的KMP算法：

def kmp_match(t, s):  # t是主串，s是模式串
    i = 0
    j = 0
    while i < len(t) and j < len(s):
        if t[i] == s[j]:
            i += 1
            j += 1
        else:
            j = next[j]
    if j == len(s):
        return i-len(s)
    else:
        return 'match failed'

现在再来回到如何求解next[j]，求解next[j]的过程很像KMP算法，仿照KMP算法我们可以写出来：

def get_next(s):
    ne_xt = list(range(len(s))) # 填充列表，只要列表长度等于s的长度
    ne_xt[0] = -1
    i = 0
    j = -1
    while i < len(s)-1:
        if j == -1 or s[i] == s[j]:
            i += 1
            j += 1
            ne_xt[i] = j
        else:
            j = ne_xt[j]
    return ne_xt

下面就是KMP算法的真正实现：

def kmp_match(t, s):
    ne_xt = get_next(s)
    i = 0
    j = 0
    while i < len(t) and j < len(s):
        if j == -1 or t[i] == s[j]:
            i += 1
            j += 1
        else:
            j = ne_xt[j]
    if j == len(s):
        return i - len(s)
    else:
        return 'match failed'

next[j]的其实还可以改进，这里不做讨论。