图像全参考评价之梯度幅度相似性偏差(GMSD)原理简介以及Python实现

梯度幅度相似性偏差(Gradient Magnitude Similarity Deviation)是2014年zhang lei等人在论文《Gradient Magnitude Similarity Deviation: A Highly Efficient Perceptual Image Quality Index》提出的一种图像全参考评价(FR-IQA)方法，具有准确度高、计算量少的特点。

• 原理简介
  梯度幅值能够反映结构信息，仅使用梯度幅值作为特征就能产生准确度较高的图片质量预测分数。自然图像往往有着丰富类型的局部结构，不同的结构在失真中会有不同的梯度幅值退化。基于局部质量退化在图像全局上的变化可以反映图像的质量这一观点，文章提出了计算局部梯度幅值相似性来衡量局部图像质量，计算局部图像质量的标准差来衡量图像全局的质量。
  1.计算局部梯度幅值相似性
  作者使用Prewitt算子计算图像梯度，使用其他算子如 Sobel and Scharr 得到的效果相似。
  
  然后计算梯度幅值mr、md：
  
  梯度幅值相似性(GMS)如下：
  
  c是一个常数，作用是为了防止分母为0.
  2.标准差池化
  SSIM等方法使用的是平均池化方法，这种方法计算简便，认为图像每块区域的质量对全局质量的贡献相同。也有研究人员提出加权池化的方法，但是这种方法对效果提升作用不大且提高了计算量。自然图像具有丰富的结构，不同结构对于失真的响应不同，如模糊在“平坦”部位的影响就比在“纹理”部位的影响小。基于局部质量退化在图像全局上的变化可以反映图像的质量这一理念，文章提出了 Standard Deviation Pooling。
  

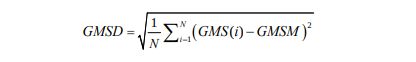
• 代码实现
  在实验应用中，文章首先使用2x2均值滤波器分别对原始图像和失真图像进行滤波，然后进行间隔为2的下采样。

论文的MATLAB源码如下：

function [score, quality_map] = GMSD(Y1, Y2)

% GMSD - measure the image quality of distorted image 'Y2' with the reference image 'Y1'.
% 
% inputs:
% 
% Y1 - the reference image (grayscale image, double type, 0~255)
% Y2 - the distorted image (grayscale image, double type, 0~255)
% 
% outputs:

% score: distortion degree of the distorted image
% quality_map: local quality map of the distorted image

% This is an implementation of the following algorithm:
% Wufeng Xue, Lei Zhang, Xuanqin Mou, and Alan C. Bovik, 
% "Gradient Magnitude Similarity Deviation: A Highly Efficient Perceptual Image Quality Index",
% http://www.comp.polyu.edu.hk/~cslzhang/IQA/GMSD/GMSD.htm

T = 170; 
Down_step = 2;
dx = [1 0 -1; 1 0 -1; 1 0 -1]/3;
dy = dx';

aveKernel = fspecial('average',2);
aveY1 = conv2(Y1, aveKernel,'same');
aveY2 = conv2(Y2, aveKernel,'same');
Y1 = aveY1(1:Down_step:end,1:Down_step:end);
Y2 = aveY2(1:Down_step:end,1:Down_step:end);

IxY1 = conv2(Y1, dx, 'same');     
IyY1 = conv2(Y1, dy, 'same');    
gradientMap1 = sqrt(IxY1.^2 + IyY1.^2);

IxY2 = conv2(Y2, dx, 'same');     
IyY2 = conv2(Y2, dy, 'same');

gradientMap2 = sqrt(IxY2.^2 + IyY2.^2);
quality_map = (2*gradientMap1.*gradientMap2 + T) ./(gradientMap1.^2+gradientMap2.^2 + T);
score = std2(quality_map);

python实现如下：

import cv2
import numpy as np
import time
from numba import jit,njit
#实现卷积操作
@jit
def convolution(img,kernal):
    new_arr = kernal.reshape(kernal.size)
    new_arr = new_arr[::-1]
    kernal = new_arr.reshape(kernal.shape)

    kernal_heigh = kernal.shape[0]
    kernal_width = kernal.shape[1]

    cor_heigh = img.shape[0] - kernal_heigh + 1
    cor_width = img.shape[1] - kernal_width + 1
    result = np.zeros((cor_heigh, cor_width), dtype=np.float64)
    for i in range(cor_heigh):
        for j in range(cor_width):
            result[i][j] = (img[i:i + kernal_heigh, j:j + kernal_width] * kernal).sum()
    return result

def gmsd(dis_img,ref_img,c=170):
    hx=np.array([[1/3,0,-1/3]]*3,dtype=np.float64)#Prewitt算子
    ave_filter=np.array([[0.25,0.25],[0.25,0.25]])#均值滤波核
    down_step=2#下采样间隔
    hy=hx.transpose()
    #均值滤波
    ave_dis=convolution(dis_img,ave_filter)
    ave_ref=convolution(ref_img,ave_filter)
    #下采样
    ave_dis_down=ave_dis[np.arange(0,ave_dis.shape[0],down_step),:]
    ave_dis_down=ave_dis_down[:,np.arange(0,ave_dis_down.shape[1],down_step)]
    ave_ref_down=ave_ref[np.arange(0,ave_ref.shape[0],down_step),:]
    ave_ref_down=ave_ref_down[:,np.arange(0,ave_ref_down.shape[1],down_step)]
    #计算mr md等中间变量
    mr_sq=convolution(ave_ref_down,hx)**2+convolution(ave_ref_down,hy)**2
    md_sq=convolution(ave_dis_down,hx)**2+convolution(ave_dis_down,hy)**2
    mr=np.sqrt(mr_sq)
    md=np.sqrt(md_sq)
    GMS=(2*mr*md+c)/(mr_sq+md_sq+c)
    GMSM=np.mean(GMS)
    GMSD=np.mean((GMS-GMSM)**2)
    return GMSD

与上面MATLAB代码不同的是，这里的二维卷积实现的是‘valid’模式。