克鲁斯卡尔（Kruskal）算法（K算法）：公交站问题

1，应用场景—公交站问题

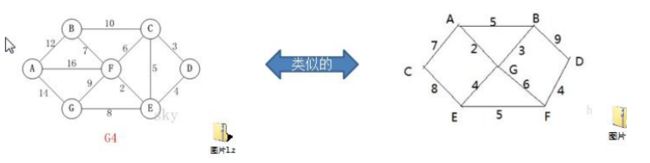
• 某城市从新增的7个站点（A，B，C，D，E，F，G），现在需要把7个站点联通
• 各个站点的距离用边权表示，比如A-B为12公里
• 如何修路保证各个站点都能走通，并距离最短
• 从图和问题可以看出，克鲁斯卡尔算法与普里姆算法解决的问题完成一致，只是解决问题的方式不同

2，克鲁斯卡尔算法介绍

• 克鲁斯卡尔算法，是用来求加权连通图的最小生成树的算法
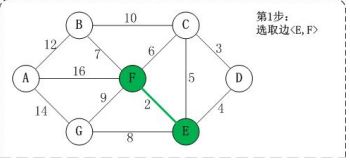
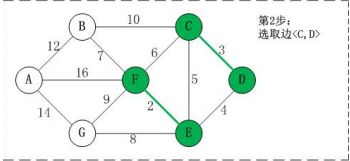
• 基本算法思想：按照边权值大小从小到大的顺序选取n - 1条边，并保证这n - 1条边不构成回路
• 回路的判断标准是连接边的两个顶点的终点重合

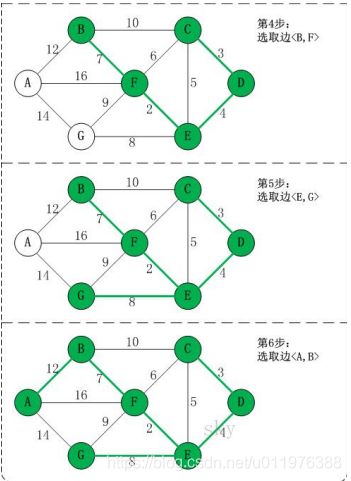
2.1，算法图解

1. 以应用场景中的左图为例

2. 第一步，取最小的边，即，权值为2
   

3. 第二步，继续取最小的边，即，权值为3
   

4. 第三步，继续取，此处注意，构成回路的标准是顶点的终点不能一致，不是按照顶点的访问记录判断
   

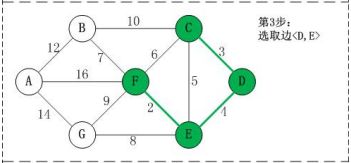
5. 紧接着，取最小的边，此处注意，构成了回路；因为将，，加入到最小生成树中后，这几个边的顶点就都了各自的终点F，此时再连接时，的终点都为F，终点重合，则构成了回路，不能构建

6. 按照第一步到第五步的逻辑，依次类推，则最后的结果如下：
   

7. 此时，最小生成树构建完成，最后的结果是，，，，，

3，代码实现

package com.self.datastructure.algorithm.kruskal;

import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.Getter;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * 克鲁斯卡尔算法
 * * 克鲁斯卡尔算法与Prim算法解决问题完全一致, 只是解决问题的方式不同
 * * 不同于Prim算法以点为基本单位, 克鲁斯卡尔以边为基本单位
 * * 先构建问题图表, 构建顶点, 并从中读取边的集合(注意不要读取两份)
 * * 然后对边按大小进行升序排列
 * * 遍历边的集合, 依次取出最小的边, 参与最小生成树的生成
 * * 分别从顶点-终点的记录数组中取出该边对应两个顶点的终点
 * * 如果终点重合说明构成了回路, 则不能构建
 * * 终点不重合, 说明还没有连接, 则继续构建
 * * 边集合遍历完成后, 整个最小生成树构建也随之完成
 * * 注意: 此处不能通过顶点已经访问来统计, 比如ABCD四个顶点, AB构成, CD构成, 此时ABCD已经全部访问, 但是不连通
 * @author pj_zhang
 * @create 2020-07-11 12:12
 **/
public class Kruskal {

    private final static int NOT_CONN = Integer.MAX_VALUE;

    public static void main(String[] args) {
        // 顶点集合
        char[] lstVertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        // 连接关系
        int[][] vertexMap = {
                {0, 12, NOT_CONN, NOT_CONN, NOT_CONN, 16, 14},
                {12, 0, 10, NOT_CONN, NOT_CONN, 7, NOT_CONN},
                {NOT_CONN, 10, 0, 3, 5, 6, NOT_CONN},
                {NOT_CONN, NOT_CONN, 3, 0, 4, NOT_CONN, NOT_CONN},
                {NOT_CONN, NOT_CONN, 5, 4, 0, 2, 8},
                {16, 7, 6, NOT_CONN, 2, 0, 9},
                {14, NOT_CONN, NOT_CONN, NOT_CONN, 8, 9, 0}
        };
        // 构建图
        MyGraph myGraph = new MyGraph(lstVertex, vertexMap);
        // 进行克鲁斯卡尔计算
        MyEdge[] result = kruskal(myGraph);
        System.out.println("最终结果如下: ");
        for (MyEdge myEdge : result) {
            System.out.println(myEdge);
        }
    }

    /**
     * 进行克鲁斯卡尔算法计算
     * @param myGraph 图表
     * @return 返回最终的连接关系
     */
    private static MyEdge[] kruskal(MyGraph myGraph) {
        // 结果集, 边的数量为顶点数量-1
        MyEdge[] result = new MyEdge[myGraph.getLstVertex().length - 1];
        int index = 0; // 记录下标位置
        // 顶点的连接终点集合, 初始化为0
        int[] endArr = new int[myGraph.getLstVertex().length];
        // 获取边集合
        MyEdge[] lstEdges = myGraph.getLstEdges();
        // 对边按权值从小到大进行排序
        sortEdges(lstEdges);
        // 对边集合进行遍历, 从最小开始取边进行最小生成树构建
        for (MyEdge myEdge : lstEdges) {
            // 获取边开始和结束的顶点
            char startVertex = myEdge.getStart();
            char endVertex = myEdge.getEnd();
            // 获取顶点对应的下标
            int startIndex = getVertexIndex(myGraph, startVertex);
            int endIndex = getVertexIndex(myGraph, endVertex);
            // 获取顶点连接串的终点, 避免构成回路
            int startEnd = getEndIndex(endArr, startIndex);
            int endEnd = getEndIndex(endArr, endIndex);
            // 如果终点值不重合, 说明不会构成回路, 则进行连接
            if (startEnd != endEnd) {
                // 对终点的终点进行延伸
                endArr[startEnd] = endEnd;
                // 记录边
                result[index++] = myEdge;
            }
        }
        System.out.println("终点数组: " + Arrays.toString(endArr));
        return result;
    }

    /**
     * 获取顶点的终点索引
     * @param endArr 终点记录数组
     * @param index 当前顶点下标
     * @return 终点下标
     */
    private static int getEndIndex(int[] endArr, int index) {
        // 如果当前顶点存在终点, 则继续去找终点的终点
        // 找到最终点, 最终返回该索引
        while (endArr[index] != 0) {
            index = endArr[index];
        }
        // 如果当前顶点的终点为0, 表示顶点的终点就是它自己, 直接返回即可
        return index;
    }

    /**
     * 获取顶点对应的下标
     * @param myGraph 图
     * @param vertex 顶点
     * @return
     */
    private static int getVertexIndex(MyGraph myGraph, char vertex) {
        for (int i = 0; i < myGraph.getLstVertex().length; i++) {
            if (myGraph.getLstVertex()[i] == vertex) {
                return i;
            }
        }
        return -1;
    }

    /**
     * 对边按权值进行排序
     * @param lstEdges
     */
    private static void sortEdges(MyEdge[] lstEdges) {
        for (int i = 0; i < lstEdges.length; i++) {
            for (int j = 0; j < lstEdges.length - 1 - i; j++) {
                if (lstEdges[j].getWeight() > lstEdges[j + 1].getWeight()) {
                    MyEdge temp = lstEdges[j];
                    lstEdges[j] = lstEdges[j + 1];
                    lstEdges[j + 1] = temp;
                }
            }
        }
    }

    /**
     * 构建图表
     */
    @Getter
    static class MyGraph {

        /**
         * 顶点数量
         */
        private int vertexCount;

        /**
         * 顶点列表
         */
        private char[] lstVertex;

        /**
         * 顶点图
         */
        private int[][] vertexMap;

        /**
         * 顶点的边集合
         */
        private MyEdge[] lstEdges;

        public MyGraph(char[] lstVertex, int[][] vertexMap) {
            this.vertexCount = lstVertex.length;
            this.lstVertex = lstVertex;
            this.vertexMap = vertexMap;
            // 记录边, 按顺序读取, 保证顺序
            List<MyEdge> lstData = new ArrayList<>(10);
            for (int i = 0; i < vertexCount; i++) {
                // 从下一位开始读, 保证不会生成重复的边
                for (int j = i + 1; j < vertexCount; j++) {
                    // 如果连接, 则进行统计
                    if (vertexMap[i][j] != NOT_CONN) {
                        lstData.add(new MyEdge(lstVertex[i], lstVertex[j], vertexMap[i][j]));
                    }
                }
            }
            lstEdges = new MyEdge[lstData.size()];
            for (int i = 0; i < lstData.size(); i++) {
                lstEdges[i] = lstData.get(i);
            }
        }

    }

    /**
     * 边对象
     */
    @Data
    @AllArgsConstructor
    static class MyEdge {

        /**
         * 起点
         */
        private char start;

        /**
         * 终点
         */
        private char end;

        /**
         * 权重
         */
        private int weight;
    }

}