【高级数据结构】 || AVL树详解(C++)
文章目录
- 【1】什么是AVL树
- 【2】为什么要引出AVL树
- 【3】AVL树的特点
- 【4】AVL树的旋转
- 单向右旋
- 单向左旋
- 双向旋转(先左后右)
- 双向旋转(先右后左)
- 【5】AVL树的结构
- 【6】AVL树的插入
- 【7】AVL树的删除
- 【8】AVL树的高度
- 【9】判断一棵二叉搜索树是不是平衡树
- 【10】判断一棵二叉树是否是平衡二叉搜索树
【1】什么是AVL树
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树
【2】为什么要引出AVL树
AVL树又称平衡的BST树,它能保证二叉树高度相对平衡,尽量降低二叉树的高度,提高搜索效率。
单纯的二叉搜索树在最坏的情况下插入查找删除等操作时间复杂度会是O(N)
请看如图:
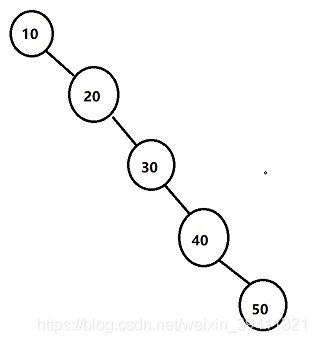
AVL树能通过几种旋转避免这种情况的发生,使得所有结点的增删改查时间复杂度为O(lg N)
【3】AVL树的特点
- 左子树和右子树的高度之差的绝对值不超过1
- 树中的每个左子树和右子树都是AVL树
- 每个节点都有一个平衡因子(balance factor),任一节点的平衡因子只能是-1,0,1
平衡因子计算方式为结点的左子树高度减去右子树的高度
【4】AVL树的旋转
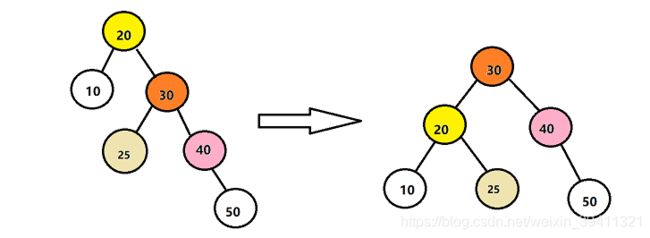
单向右旋
单向右旋平衡处理:由于在a的左子树根结点的左子树上插入结点,a的平衡因子由1增加到2,致使以a为根结点的子树失去平衡,则需要进行一次右向顺时针旋转操作。

// 右旋转操作
AVLNode* rightRotate(AVLNode* node)
{
AVLNode* child = node->_left; // 得到旋转后的根节点
node->_left = child->_right; // 该根节点的右子树则变成其原父节点的左子树
child->_right = node;// 该根节点的原父节点变成该节点的右子树
node->_height = maxHeight(node->_left, node->_right) + 1; // 更新节点高度
child->_height = maxHeight(child->_left, child->_right) + 1;// 更新节点高度
return child;//返回旋转后的根节点
}
单向左旋
单向左旋平衡处理:由于在a的右子树根结点的右子树上插入结点,a的平衡因子由-1增加到-2,致使以a为根结点的子树失去平衡,则需要进行一次左向逆时针旋转操作。
// 以node为根节点进行左旋转,返回旋转后的根节点
AVLNode* leftRotate(AVLNode* node)
{
AVLNode* child = node->_right;// 得到旋转后的根节点
node->_right = child->_left;// 该根节点的左子树则变成其原父节点的右子树
child->_left = node;// 该根节点的原父节点变成该节点的左子树
node->_height = maxHeight(node->_left, node->_right) + 1; // 更新节点高度
child->_height = maxHeight(child->_left, child->_right) + 1; // 更新节点高度
return child; //返回旋转后的根节点
}
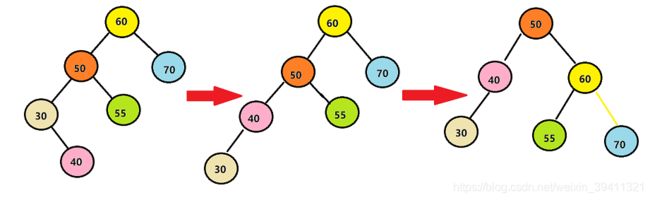
双向旋转(先左后右)
双向旋转(先左后右)平衡处理:由于在a的左子树的根结点的右子树上插入结点,a的平衡因子由1增加到2,致使a为根结点的子树失去平衡,则需要进行两次旋转(先左旋后右旋)操作。简称LR型旋转
// 左平衡 左-右旋转
AVLNode* leftBalance(AVLNode *node)
{
node->_left = leftRotate(node->_left);
return rightRotate(node);
}
双向旋转(先右后左)
双向旋转(先右后左)平衡处理:由于在a的右子树的根结点的左子树上插入结点,a的平衡因子由1增加到2,致使a为根结点的子树失去平衡,则需要进行两次旋转(先右旋后左旋)操作。简称RL型旋转

// 右平衡 右-左旋转
AVLNode* rightBalance(AVLNode *node)
{
node->_right = rightRotate(node->_right);
return leftRotate(node);
}
【5】AVL树的结构
struct AVLNode
{
AVLNode(T data = T())
:_data(data)
, _left(nullptr)
, _right(nullptr)
, _height(1)
{}
T _data; //数据域
AVLNode *_left; //左孩子
AVLNode *_right; //右孩子
int _height; //节点的高度
};
【6】AVL树的插入
void insert(const T &val)
{
_root = insert(_root, val);
}
AVLNode* insert(AVLNode *node, const T &val)
{
if (node == nullptr)
{
return new AVLNode(val);
}
if (node->_data > val)
{
node->_left = insert(node->_left, val);
// AVL添加的节点失衡判断
if (height(node->_left) - height(node->_right) > 1)
{
if (height(node->_left->_left) >= height(node->_left->_right))
{
// 左孩子的左子树太高
node = rightRotate(node);
}
else
{
// 左孩子的右子树太高
node = leftBalance(node);
}
}
}
else if (node->_data < val)
{
node->_right = insert(node->_right, val);
// AVL添加的节点失衡判断
if (height(node->_right) - height(node->_left) > 1)
{
if (height(node->_right->_right) >= height(node->_right->_left))
{
// 右孩子的右子树太高
node = leftRotate(node);
}
else
{
// 右孩子的左子树太高
node = rightBalance(node);
}
}
}
else
{
;
}
// 在递归回溯过程中,更新节点的高度值
node->_height = maxHeight(node->_left, node->_right) + 1;
return node;
}
【7】AVL树的删除
void remove(const T &val)
{
_root = remove(_root, val);
}
AVLNode* remove(AVLNode *node, const T &val)
{
if (node == nullptr)
{
return nullptr;
}
if (node->_data > val)
{
node->_left = remove(node->_left, val);
if (height(node->_right) - height(node->_left) > 1)
{
if (height(node->_right->_right) >= height(node->_right->_left))
{
// 右孩子的右子树太高
node = leftRotate(node);
}
else
{
// 右孩子的左子树太高
node = rightBalance(node);
}
}
}
else if (node->_data < val)
{
node->_right = remove(node->_right, val);
if (height(node->_left) - height(node->_right) > 1)
{
if (height(node->_left->_left) >= height(node->_left->_right))
{
// 左孩子的左子树太高
node = rightRotate(node);
}
else
{
// 左孩子的右子树太高
node = leftBalance(node);
}
}
}
else
{
if (node->_left != nullptr && node->_right != nullptr)
{
if (height(node->_left) >= height(node->_right))
{
// 前驱替换
AVLNode *pre = node->_left;
while (pre->_right != nullptr)
{
pre = pre->_right;
}
node->_data = pre->_data;
node->_left = remove(node->_left, pre->_data);
}
else
{
// 后继替换
AVLNode *post = node->_right;
while (post->_left != nullptr)
{
post = post->_left;
}
node->_data = post->_data;
node->_right = remove(node->_right, post->_data);
}
}
else
{
if (node->_left != nullptr)
{
AVLNode *left = node->_left;
delete node;
return left;
}
else if (node->_right != nullptr)
{
AVLNode *right = node->_right;
delete node;
return right;
}
else
{
return nullptr;
}
}
}
// 在递归回溯过程中,更新节点的高度值
node->_height = maxHeight(node->_left, node->_right) + 1;
return node;
}
【8】AVL树的高度
//树的高度
int level()
{
return level(_root);
}
int level(AVLNode* node)
{
if (node == nullptr)
{
return 0;
}
int left = level(node->_left);
int right = level(node->_right);
return (left > right ? left : right) + 1;
}
【9】判断一棵二叉搜索树是不是平衡树
/*
* 判断一棵 二叉搜索树 是否是 平衡树
* 因为题目条件已经说明了该树是一棵二叉搜索树
* 因此我们直接从二叉搜索树与平衡二叉搜索树在性质上的重要区别入手,即一颗
* 平衡二叉搜索树任一结点的左右子树高度差不超过1,因此我们借助了求层数的函数
* level(),在函数递归前判断是否满足该条件即可,若不满足,我们直接结束,若满足
* 继续递归遍历其他结点即可。
*/
bool isAVL()
{
return isAVL(_root);
}
bool isAVL(AVLNode *node)
{
if (node == nullptr)
{
return true;
}
if (abs(level(node->_left) - level(node->_right)) > 1)
{
return false;
}
return isAVL(node->_left) && isAVL(node->_right);
}
【10】判断一棵二叉树是否是平衡二叉搜索树
/*
* 判断一颗 二叉树 是否是 平衡二叉搜索树,是返回true,否则返回false
* 我们之前有写过判断一颗二叉树是否是二叉搜索树(BST)的代码
* 我们在递归函数前进行很多的条件判断,那么我们只需要在这部分继续添加条件
* 判断是否是平衡树即可。判断方式和上题是相同的。
*/
bool isAVLTree()
{
return isAVLTree(_root);
}
bool isAVLTree(AVLNode* node)
{
static AVLNode* prev = nullptr;
if (node == nullptr)
{
return true;
}
if (!isAVLTree(node->_left))
{
return false;
}
if (prev != nullptr && node->_data < prev->_data)
{
return false;
}
if (abs(level(node->_left) - level(node->_right)) > 1)
{
return false;
}
prev = node;
return isAVLTree(node->_right);
}