并查集分析

以下内容整理至 《挑战程序设计竞赛》

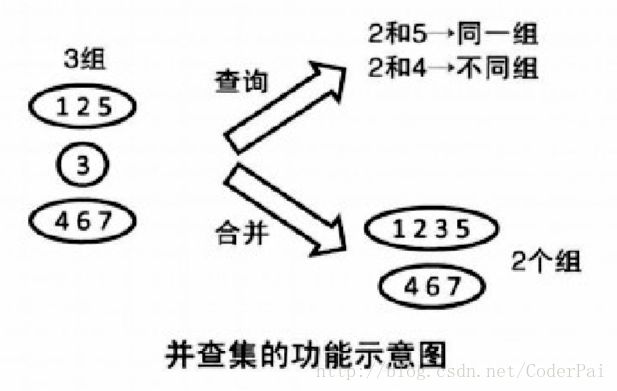
1. 并查集是什么

并查集是一种用来管理元素分组情况的数据结构。并查集可以高效地进行如下操作。不过需要注意并查集虽然可以进行合并操作，但是却无法进行分割操作。

• 查询元素 a 和元素 b 是否属于同一组。
• 合并元素 a 和元素 b 所在的组。

2. 并查集操作

2.1 初始化

我们准备 n 个节点来表示 n 个元素。最开始时没有边。

程序实现如下：

for(int i=0; ii++)
    path[i] = i;

2.2 节点查询

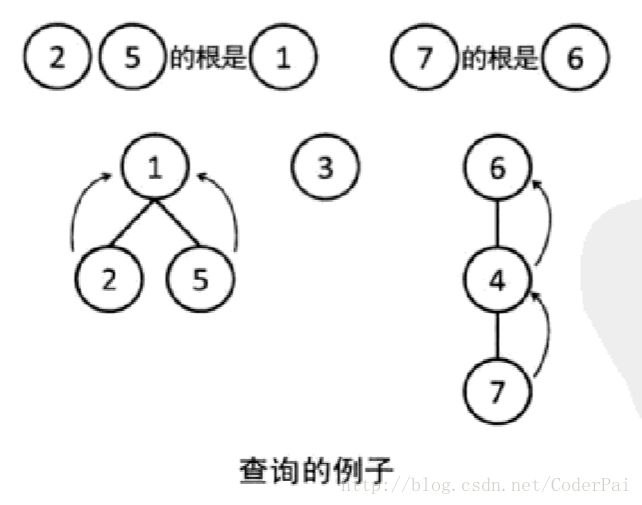
为了查询两个节点是否属于同一组，我们需要沿着树向上走，来查询包含这个元素的树的根是谁。如果两个节点走到了同一个根，那么就可以知道它们属于同一组。

在下图中，元素 2 和元素 5 都走到了元素 1，因此它们属于同一组。另一方面，由于元素 7 走到的是元素 6，因此同元素 2 或元素 5 属于不同组。

程序实现如下：

// 寻找节点 x 的根节点
int find(int x)
{
    int r=x;
    while( pre[r] != r )
          r=pre[r];
    return r;
}

2.3 合并操作

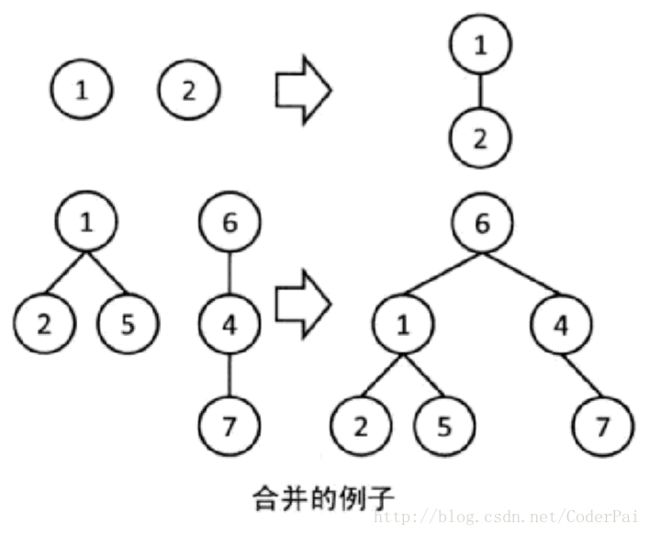
像下图一样，从一个组的根向另一个组的根连边，这样两棵树就变成了一棵树，也就把两个组合合并为一个组了。

程序实现如下：

void merge(int a,int b)
{
    int fa=find(a),fb=find(b);
    if(fa!=fb)
        path[fx] = fy;
}

至此，我们实现了基础的并查集初始化，查找和合并操作。但是这样操作会导致并查集退化，甚至退化到线性。那么，有没有办法避免这种情况呢？答案是肯定的，我们可以在查找操作和合并操作的时候做一些小优化。

3. 并查集优化

3.1 合并优化

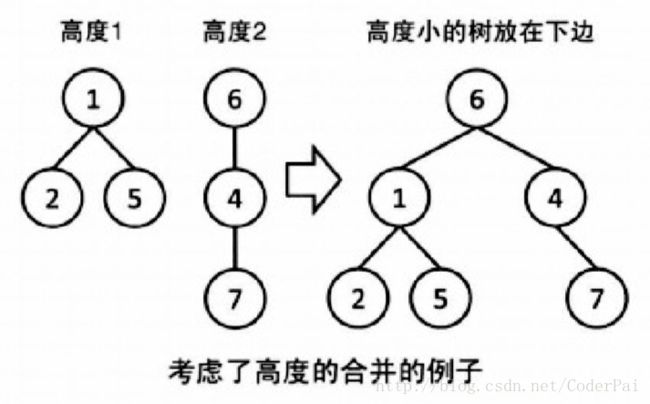
当我们在进行合并操作的时候，上面的代码并没有去对比树的高度。那么，就会造成这样一种问题，我们会把一颗子树一直归并到另一个固定的树，从而把树变成了线性结构。为了解决这个问题，我们可以按照如下操作：

• 对于每棵树，记录这棵树的高度（rank）。
• 合并时如果两棵树的 rank 不同，那么从 rank 小的向 rank 大的合并。

程序实现如下：

void merge(int a,int b)
{
    int fa=find(a),fb=find(b);
    if(faelse
        path[fa]=fb;
}

3.2 路径压缩

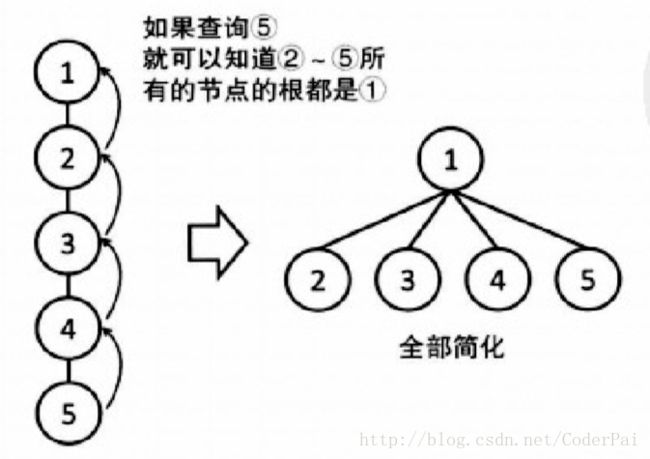
当我们在合并两个节点的时候，有一种路径压缩算法可以提高查询效率。具体的压缩算法是，对于每个节点，一旦向上走到了一次根节点，就把这个点到父亲的边改为直接连向根。比如下图的2~5个节点，所有的根节点都是1，如下：

程序实现如下：

int find(int x)
{
    int r=x;
    while(r!=path[r])
        r=path[r];
    int i=r,j=-1;

    while(i!=j)
    {
        j=path[i];  // 在改变上级之前，用临时变量 j 记录下他的值
        path[i]=r;  // 把上级节点改为根节点
        i=j;
    }
    return r;
}

4. 并查集的复杂度

加入了这两个优化之后的并查集效率非常之高。对 n 个元素的并查集进行一次操作的复杂度是 O(a(n))。在这里，a(n) 是阿克曼（Ackermann）函数的反函数。这比 O(log(n)) 还要快。

不过，这是“均摊复杂度”。也就是说，并不是每一次操作都满足这个复杂度，而是多次操作之后平均每一次操作的复杂度是 O(a(n)) 的意思。

5. 并查集的完整实现

在例子中，我们用编号代表每个元素。数据 path 表示的是父亲的编号，path[x] = x 时，x 是所在的树的根。

int path[100];
int rank[100];

// 初始化 n 个元素
void init(int n)
{
    for (int i=0; i0;
    }
}

// 查询树的根
int find(int x)
{
    int r=x;
    while(r!=path[r])
        r=path[r];
    int i=r,j=-1;

    while(i!=j)
    {
        j=path[i];  // 在改变上级之前，用临时变量 j 记录下他的值
        path[i]=r;  // 把上级节点改为根节点
        i=j;
    }
    return r;
}

// 合并 x 和 y 所属的合集
void merge(int x, int y)
{
    fx = find(x);
    fy = find(y);
    if (fx == fy) return;
    if (rank[fx] < rank[fy])
        path[fx] = fy;
    else
    {
        path[fy] = fx;
        if (rank[fx] == rank[fy]) rank[fx] ++;
    }
}

---

如果觉得内容有用，帮助多多分享哦 :)

长按或者扫描如下二维码，关注 “CoderPai” 微信号（coderpai）。添加底部的 coderpai 小助手，添加小助手时，请备注 “算法” 二字，小助手会拉你进算法群。如果你想进入 AI 实战群，那么请备注 “AI”，小助手会拉你进AI实战群。