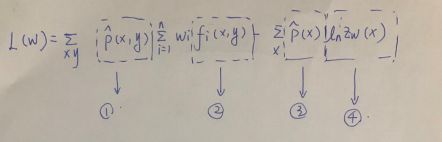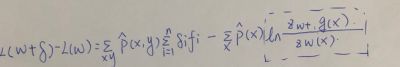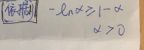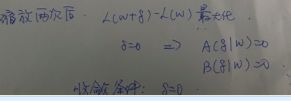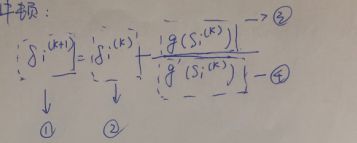AI-统计学习(11)-改进的迭代算法及拟牛顿法

   逻辑回归时是需要改进迭代尺度算法，用于提高收敛性，而对于没有显示形式方程求极值或者0时，我们需要用拟牛顿法。

1.改进的尺度迭代算法

   1.1公式及解释

   1.2求解步骤及难点说明

      1.2.1.第一次缩放

        1.2.2第二次缩放

   1.3收敛条件

   1.4总结

2.拟牛顿法步骤

    2.1公式及解释

   2.2图形及步骤说明

---

 

1.改进的尺度迭代算法

1.1公式及解释

  公式

  1.1.1x,y的经验分布函数

  1.1.2 f(x,y)给出的特征函数，每给出一对（x,y） f应该是知道的。

1.1.3 p(x) 对x 的经验分布，给一个x就去训练集中找x，在训练集中的比例是多少

1.1.4lnzw(x) 给定xy的条件分布的一个归一化的系数

1.2目标是求极值，求解步骤及难点说明

  1.2.1 步骤：w赋初值，然后更新w ,使wifi增大，从而求最大值。

  1.2. 2难的部分就是指数上有w, 还要做对数变化。于是经历两次缩放。

   1.2 3依据1：

           

实现第一次缩放记作：

      

   1.2.4 依据2:

          

实现第二次缩放记作

        

两次缩放以后

        

 1.3收敛条件

        

1.4总结

  1.4.1目的是找到似然函数增大最大的

   1.4.2 找到下界

   1.4.3 最大化下界

   1.4.4难点就是参数需要存在指数求导，变换后还存在指数求导，于是两次缩放

 

 

2.拟牛顿法步骤

 2.1 公式及解释

解释：1.当前步的值

         2.前一步的值

        3.前一步的函数

         4.前一步函数导数

 2.2图形及步骤说明