常见的数据结构与算法

一，数据结构

       我们如何把现实中大量而且非常复杂的问题以特定的数据类型(个体)和特定的存储结构(个体的关系)保存到相应的主存储器(内存)中，以及在此基础上为实现某个功能而执行的相应操作，这个相应的操作也叫做算法。简单来说：

     数据结构 == 个体 + 个体的关系
     算法 == 对存储数据的操作

 

二，衡量算法的标准

• 时间复杂度 指的是大概程序执行的次数，而非程序执行的时间
• 空间复杂度 指的是程序执行过程中，大概所占有的最大内存
• 难易程度
• 健壮性

三，常见的几种数据排序

• 冒泡排序
• 选择排序
• 插入排序
• 快速排序

###冒泡排序

def bubble_sort(li):
    for i in range(len(li)-1):
        for j in range(len(li)-i-1):
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j]



###选择排序

def select_sort(li):
    for i in range(len(li)-1):
        min_loc = i
        for j in range(i+1,len(li)):
            if li[j] < li[min_loc]:
                min_loc = j
        if min_loc != i:
            li[i],li[min_loc] = li[min_loc],li[i]



###插入排序（二分法）

def insert_sort(li):
    for i in range(1,len(li)):
        tmp = li[i]
        j = i-1

        while j >=0 and tmp 
    
####快速排序
def quick_sort(data, left, right):
     if left < right:
         mid = partition(data, left, right)
         quick_sort(data, left, mid - 1)
         quick_sort(data, mid + 1,right)


def partition(data, left, right):
    tmp = data[left]
    while left < right:
       while left < right and data[right] >= tmp:
             right -= 1
       data[left] = data[right]
       while left < right and data[left] <= tmp:
             left += 1
       data[right] = data[left]
    data[left] = tmp
    return left
 
    
 
      
    
 
   

     常见的查找方法：

              顺序查找

             二分查找

     应用场景：

           各种榜单

           各种表格

           给二分法查找用

 

四，线性结构

        线性结构就是把诺干个数据节点用一条线串联起来

        1，连续储存（数组）：python中的列表

• 优点:
  • 存取速度快
• 缺点：
  • 事先需要知道数组的长度
  • 需要大块的连续内存
  • 插入删除非常的慢，效率极低

 

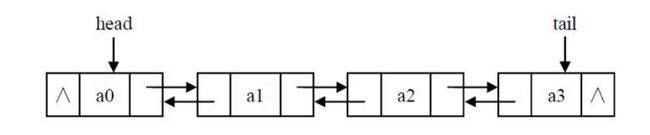
        2，离散储存（链表）：

定义：

• n个节点离散分配
• 彼此通过指针相连
• 每个节点只有一个前驱节点，每个节点只有一个后续节点
• 首节点没有前驱节点，尾节点没有后续节点

优点:

• 空间没有限制，插入删除元素很快

缺点：

• 查询比较慢

链表的节点的结构如下：

值	指针域
data	next

 

data为自定义的数据，next为下一个节点的地址。

2.专业术语：

• 首节点：第一个有效节点
• 尾节点：最后一个有效节点
• 头结点：第一个有效节点之前的那个节点，头结点并不存储任何数据，目的是为了方便对链表的操作
• 头指针：指向头结点的指针变量
• 尾指针：指向尾节点的指针变量

3.链表的分类：

• 单链表
• 双链表 每一个节点有两个指针域
• 循环链表 能通过任何一个节点找到其他所有的节点
• 非循环链表

4.算法：

• 增加
• 删除
• 修改
• 查找
• 总长度

5，链表的增删改操作

      如果希望通过一个函数来对链表进行处理操作，只需要一个参数，头结点即可，因为我们可以通过头结点来推算出链表的其他所有的参数

class Hero(object):
    def __init__(self, no=None, nickname=None, name=None, pNext = None):
        self.no = no
        self.nickname = nickname
        self.name = name
        self.pNext = pNext


def addHero(head, pNew):
    cur = head
    # while cur.pNext != None:
    #     cur = cur.pNext
    #
    # cur.pNext = pNew

    while cur.pNext != None:
        if cur.pNext.no > pNew.no:
            break

        cur = cur.pNext

    pNew.pNext = cur.pNext
    cur.pNext = pNew

def showHero(head):
    if isEmpty(head):
        return None

    cur = head

    while cur.pNext != None:
        print("英雄的编号是: %s, 外号是：%s, 姓名:%s" % (cur.pNext.no, cur.pNext.nickname, cur.pNext.name))
        cur = cur.pNext

def isEmpty(head):
    if head.pNext != None:
        return False
    return True

def delHero(head,no):
    cur = head
    while cur.pNext != None:
        if cur.pNext.no == no:
            cur.pNext = cur.pNext.pNext
            break
        cur = cur.pNext





# 头结点
head = Hero()

## 首节点
h1 = Hero(1, '及时雨', '宋江')
h2 = Hero(2, '玉麒麟', '卢俊义')
h3 = Hero(6, '豹子头', '林冲')
h4 = Hero(4, '入云龙', '公孙胜')

addHero(head, h1)
addHero(head, h2)
addHero(head, h3)
addHero(head, h4)

showHero(head)

View Code

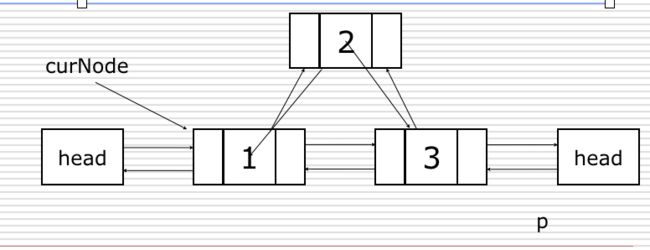
6，双向链表操作：

双向链表中每个节点有两个指针：一个指向后面节点、一个指向前面节点

class Node(object):
      def __init__(self, data=None):
           self.data = data
           self.next = None
           self.prior = None

 

插入：双向链表的操作：

p.next = curNode.next
curNode.next.prior = p
curNode.next = p
p.prior = curNode

 

删除：

p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p

 

8.循环链表

     循环链表是另一种形式的链式存贮结构。它的特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。

   利用循环链表解决约瑟夫问题：

    设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类推，直到所有人出列为止，由此产生       一个出队编号的序列

###循环链表
class Child(object):
    first = None
    def __init__(self, no=None, pNext=None):
        self.no = no
        self.pNext = pNext

    def addChild(self, n):
        cur = None
        for i in range(n):      #创建n个元素
            child = Child(i + 1)

            if i == 0 :       #循环链表
                self.first = child
                child.pNext = self.first
                cur = self.first
            else:
                cur.pNext = child
                child.pNext = self.first
                cur = cur.pNext

    def showChild(self):
        cur = self.first
        while cur.pNext != self.first:
            print("当前孩子的编号是：%s" % cur.no)
            cur = cur.pNext

        print("当前孩子的编号是：%s" % cur.no)

    def countChild(self, m, k):
        tail = self.first

        while tail.pNext != self.first:
            tail = tail.pNext

        #### 当退出循环的时候，tail已经是在first的后面了

        for i in range(k-1):
            tail = tail.pNext
            self.first = self.first.pNext

        while tail != self.first:
            for i in range( 1):
                tail = tail.pNext
                self.first = self.first.pNext

            self.first = self.first.pNext
            tail.pNext = self.first

        print("最终剩下的孩子的编号是: %s" % self.first.no)



c = Child()
c.addChild(1000)
c.showChild()
c.countChild(3,2)

      线性结构的两种应用之栈：

          栈的定义：是一种先进后出的储存方式

结构类似箱子，先放进去的最后出

 

栈的分类：静态与动态

• 静态栈

  • 静态栈的核心是数组，类似于一个连续内存的数组，我们只能操作其栈顶元素

• 动态栈

  • 动态栈的核心是链表

 

 

栈的算法主要是压栈和出栈两种操作的算法，下面我就用代码来实现一个简单的栈。

首先要明白以下思路：

• 栈操作的是一个一个节点
• 栈本身也是一种存储的数据结构
• 栈有初始化、压栈、出栈、判空、遍历、清空等主要方法

class Stack(object):
    def __init__(self):
        self.pTop = None
        self.pBottom = None

class Node(object):
    def __init__(self, data=None, pNext = None):
        self.data = data
        self.pNext = pNext


def push(s, new):
    new.pNext = s.pTop
    s.pTop = new


def pop(s):
    cur = s.pTop

    while cur != s.pBottom:
        s.pTop = cur.pNext
        print("出栈的元素是: %d" % cur.data)
        cur = cur.pNext
    else:
        print("出栈失败")
def getAll(s):
    cur = s.pTop
    while cur != s.pBottom:
        print(cur.data)
        cur = cur.pNext
def is_empty(s):
    if s.pTop == s.pBottom:
        return True
    else:
        return False
def clear(s):
    if is_empty(s):
        return None
    p = s.pTop
    q = None
    while p != s.pBottom:
        q = p.pNext
        del p
        p = q
    else:
        s.pBottom = s.pTop
head = Node()
s = Stack()
s.pTop = s.pBottom = head
n1 = Node(2)
push(s, n1)
n1 = Node(5)
push(s, n1)
n1 = Node(89)
push(s, n1)
print("##############遍历元素##########")
getAll(s)
# print("##############出栈元素#######")
# pop(s)
print("##############清空栈##########")
clear(s)
print("##############遍历元素##########")
getAll(s)

      栈的一些应用：

            函数的调用

            内存的分配

            表达式求值

            ......

 

线性结构的两种应用之队列：

   队列的定义：是一种先进先出的数据存储结构

  

   队列的分类：链式队列与静态队列

  链式队列的算法：

class Node:
    def __init__(self, value):
        self.data = value
        self.next = None
class Queue:
    def __init__(self):
        self.front = Node(None)
        self.rear = self.front
    def enQueue(self, element):
        n = Node(element)
        self.rear.next = n
        self.rear = n
    def deQueue(self):
        if self.empty():
            print('队空')
            return
        temp = self.front.next
        self.front = self.front.next
        if self.rear == temp:
            self.rear = self.front
        del temp
    def getHead(self):
        if self.empty():
            print('队空')
            return
        return self.front.next.data
    def empty(self):
        return self.rear == self.front
    def printQueue(self):
        cur = self.front.next
        while cur != None:
            print(cur.data)
            cur = cur.next
    def length(self):
        cur = self.front.next
        count = 0
        while cur != None:
            count += 1
            cur = cur.next
        return count
if __name__ == '__main__':
    queue = Queue()
    queue.enQueue(23)
    queue.enQueue(2)
    queue.enQueue(4)
    queue.printQueue()
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)

队列的实际应用：

      最经典的应用是：生产者与消费者模型

Python的Queue模块中提供了同步的、线程安全的队列类，包括FIFO（先入先出)队列Queue，LIFO（后入先出）队列LifoQueue，和优先级队列PriorityQueue。这些队列都实现了锁原语（可以理解为原子操作，即要么不做，要么就做完），能够在多线程中直接使用。可以使用队列来实现线程间的同步。

用FIFO队列实现上述生产者与消费者问题的代码如下：

import threading
import time
 
#python2中
from Queue import Queue
 
#python3中
# from queue import Queue
 
class Producer(threading.Thread):
    def run(self):
        global queue
        count = 0
        while True:
            if queue.qsize() < 1000:
                for i in range(100):
                    count = count +1
                    msg = '生成产品'+str(count)
                    queue.put(msg)
                    print(msg)
            time.sleep(0.5)
 
class Consumer(threading.Thread):
    def run(self):
        global queue
        while True:
            if queue.qsize() > 100:
                for i in range(3):
                    msg = self.name + '消费了 '+queue.get()
                    print(msg)
            time.sleep(1)
 
 
if __name__ == '__main__':
    queue = Queue()
 
    for i in range(500):
        queue.put('初始产品'+str(i))
    for i in range(2):
        p = Producer()
        p.start()
    for i in range(5):
        c = Consumer()
        c.start()

queue的说明：

1. 对于Queue，在多线程通信之间扮演重要的角色
2. 添加数据到队列中，使用put()方法
3. 从队列中取数据，使用get()方法
4. 判断队列中是否还有数据，使用qsize()方法

• 为什么要使用生产者和消费者模式

在线程世界里，生产者就是生产数据的线程，消费者就是消费数据的线程。在多线程开发当中，如果生产者处理速度很快，而消费者处理速度很慢，那么生产者就必须等待消费者处理完，才能继续生产数据。同样的道理，如果消费者的处理能力大于生产者，那么消费者就必须等待生产者。为了解决这个问题于是引入了生产者和消费者模式。

• 什么是生产者消费者模式

生产者消费者模式是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯，而通过阻塞队列来进行通讯，所以生产者生产完数据之后不用等待消费者处理，直接扔给阻塞队列，消费者不找生产者要数据，而是直接从阻塞队列里取，阻塞队列就相当于一个缓冲区，平衡了生产者和消费者的处理能力。

这个阻塞队列就是用来给生产者和消费者解耦的。纵观大多数设计模式，都会找一个第三者出来进行解耦

 

转载于:https://www.cnblogs.com/liqingxiaobai/articles/9588181.html