三次样条曲线拟合及Matlab/Python实现

对于形如y = a + bx + c * x^2 + d * x^3 的三次spline曲线拟合的数学原理，我就不多说了。

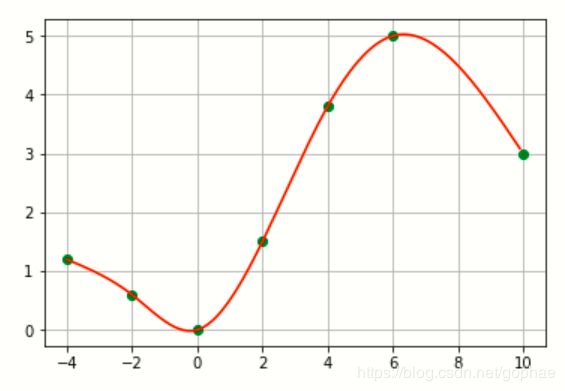
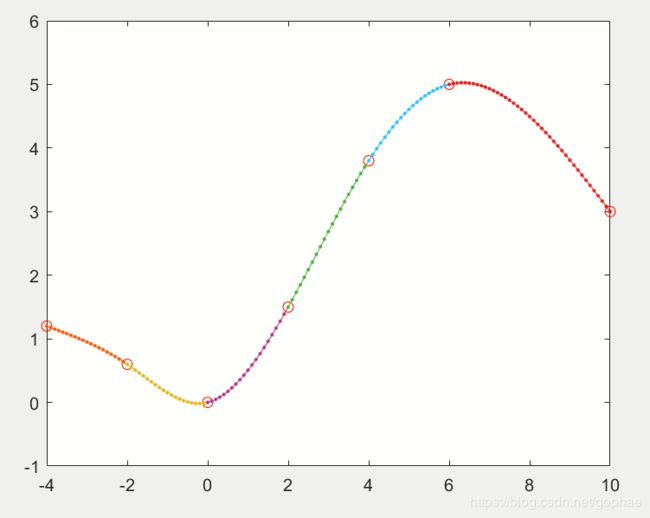
我接了一个图给大家看看：




数值计算的伪代码如下：

书名是：numerical_methods_for_engineers_for_engineers_chapra_canale_6th_edition
spline interpolation 在18.6章，想了解如何做三次曲线拟合的就去这个书里面找一下。

接下来就是Matlab 和 Python的实现：
Python代码来自https://github.com/gameinskysky/PythonRobotics/tree/master/PathPlanning/FrenetOptimalTrajectory
我稍作了修改：

class Spline:
    u"""
    Cubic Spline class
    """

    def __init__(self, x, y):
        self.b, self.c, self.d, self.w = [], [], [], []

        self.x = x
        self.y = y

        self.nx = len(x)  # dimension of x
        h = np.diff(x)

        # calc coefficient c
        self.a = [iy for iy in y]

        # calc coefficient c
        A = self.__calc_A(h)
        B = self.__calc_B(h)
        self.c = np.linalg.solve(A, B)
        #  print(self.c1)

        # calc spline coefficient b and d
        for i in range(self.nx - 1):
            self.d.append((self.c[i + 1] - self.c[i]) / (3.0 * h[i]))
            tb = (self.a[i + 1] - self.a[i]) / h[i] - h[i] * \
                (self.c[i + 1] + 2.0 * self.c[i]) / 3.0
            self.b.append(tb)

    def calc(self, t):
        u"""
        Calc position
        if t is outside of the input x, return None
        """

        if t < self.x[0]:
            return None
        elif t > self.x[-1]:
            return None

        i = self.__search_index(t)
        dx = t - self.x[i]
        result = self.a[i] + self.b[i] * dx + \
            self.c[i] * dx ** 2.0 + self.d[i] * dx ** 3.0

        return result

    def calcd(self, t):
        u"""
        Calc first derivative
        if t is outside of the input x, return None
        """

        if t < self.x[0]:
            return None
        elif t > self.x[-1]:
            return None

        i = self.__search_index(t)
        dx = t - self.x[i]
        result = self.b[i] + 2.0 * self.c[i] * dx + 3.0 * self.d[i] * dx ** 2.0
        return result

    def calcdd(self, t):
        u"""
        Calc second derivative
        """

        if t < self.x[0]:
            return None
        elif t > self.x[-1]:
            return None

        i = self.__search_index(t)
        dx = t - self.x[i]
        result = 2.0 * self.c[i] + 6.0 * self.d[i] * dx
        return result

    def __search_index(self, x):
        u"""
        search data segment index
        """
        return bisect.bisect(self.x, x) - 1

    def __calc_A(self, h):
        u"""
        calc matrix A for spline coefficient c
        """
        A = np.zeros((self.nx, self.nx))
        A[0, 0] = 1.0
        for i in range(self.nx - 1):
            if i != (self.nx - 2):
                A[i + 1, i + 1] = 2.0 * (h[i] + h[i + 1])
            A[i + 1, i] = h[i]
            A[i, i + 1] = h[i]

        A[0, 1] = 0.0
        A[self.nx - 1, self.nx - 2] = 0.0
        A[self.nx - 1, self.nx - 1] = 1.0
        #  print(A)
        return A

    def __calc_B(self, h):
        u"""
        calc matrix B for spline coefficient c
        """
        B = np.zeros(self.nx)
        for i in range(self.nx - 2):
            B[i + 1] = 3.0 * (self.a[i + 2] - self.a[i + 1]) / \
                h[i + 1] - 3.0 * (self.a[i + 1] - self.a[i]) / h[i]
        #  print(B)
        return B


class Spline2D:
    u"""
    2D Cubic Spline class
    """

    def __init__(self, x, y):
        self.s = self.__calc_s(x, y)
        self.sx = Spline(self.s, x)
        self.sy = Spline(self.s, y)

    def __calc_s(self, x, y):
        dx = np.diff(x)
        dy = np.diff(y)
        self.ds = [math.sqrt(idx ** 2 + idy ** 2)
                   for (idx, idy) in zip(dx, dy)]
        s = [0]
        s.extend(np.cumsum(self.ds))
        return s

    def calc_position(self, s):
        u"""
        calc position
        """
        x = self.sx.calc(s)
        y = self.sy.calc(s)

        return x, y

    def calc_curvature(self, s):
        u"""
        calc curvature
        """
        dx = self.sx.calcd(s)
        ddx = self.sx.calcdd(s)
        dy = self.sy.calcd(s)
        ddy = self.sy.calcdd(s)
        k = (ddy * dx - ddx * dy) / (dx ** 2 + dy ** 2)
        return k

    def calc_yaw(self, s):
        u"""
        calc yaw
        """
        dx = self.sx.calcd(s)
        dy = self.sy.calcd(s)
        yaw = math.atan2(dy, dx)
        return yaw


def calc_spline_course(x, y, ds=0.1):
    sp = Spline2D(x, y)
    s = list(np.arange(0, sp.s[-1], ds))

    rx, ry, ryaw, rk = [], [], [], []
    for i_s in s:
        ix, iy = sp.calc_position(i_s)
        rx.append(ix)
        ry.append(iy)
        ryaw.append(sp.calc_yaw(i_s))
        rk.append(sp.calc_curvature(i_s))

    return rx, ry, ryaw, rk, s

然后再写一个test文件：

import sys;
sys.path.append("H:\Project\TrajectoryPlanningModelDesign\Codes\frenet_optimal\frenet_optimal")#这里写你存放上面这个文件的文件夹目录
import cubic_spline
import numpy as np
import matplotlib.pyplot as plt
x = [-4 ,-2, 0, 2, 4, 6, 10];
y = [1.2, 0.6, 0, 1.5, 3.8, 5, 3];
spline = cubic_spline.Spline(x,y)
rx = np.arange(-4,10,0.1)
ry = [spline.calc(i) for i in rx]
plt.plot(x,y,"og")
plt.plot(rx,ry,"-r")
plt.grid(True)
#因为在jupyter 里面写的，最开始调用一下import sys

结果如图：

把python写成Matlab

clc
clear all

x = [-4 -2 0 2 4 6 10];
    y = [1.2 0.6 0 1.5 3.8 5 3];
    figure
    plot(x,y,'ro');
    hold on
    
    N = length(x);
   A = zeros(N,N);
   B = zeros(N,1);

   for i = 1:N-1
   h(i) = x(i+1) - x(i);
   end
   
   A(1,1) = 1; 
   A(N,N) = 1;
   for i = 2:N-1
       A(i,i) = 2*(h(i-1) + h(i));
   end
   
   for i  =2 : N-1
   A(i, i+1) = h(i);
   end
   
   for i  = 2: N-1
       A(i,i-1) = h(i-1);
   end
   
   for i = 2:N-1
       B(i) = 6* (y(i+1)-y(i))/h(i) - 6* (y(i)-y(i-1))/h(i-1);
   end
   m= A\B
   
   for i = 1:N
       a(i) = y(i);
   end
   
     for i = 1:N
       c(i) = m(i)/2;
     end
   
      for i = 1:N-1
          d(i) =( c(i+1)-c(i) )/(3*h(i));
      end
      
       for i = 1:N-1
           b(i)  = (a(i+1)-a(i))/h(i)- h(i)/3*(c(i+1)+ 2*c(i));
       end
       
       for  i= 1:N-1
           X = x(i):0.1:x(i+1);
           Y = a(i)+ b(i)*(X-x(i)) + c(i) * (X- x(i)).^2 + d(i) * (X - x(i)).^3;
       plot(X, Y,'.-')   
       end
         

结果如图：