NOIP 提高组 初赛 三、问题求解 习题集(三)NOIP2006-NOIP2009
1.第十二届(NOIP2006)
问题:
1.将 2006 个人分成若干不相交的子集,每个子集至少有 3 个人,并且:
(1)在每个子集中,没有人认识该子集的所有人。
(2)同一子集的任何 3 个人中,至少有 2 个人互不认识。
(3)对同一子集中任何 2 个不相识的人,在该子集中恰好只有 1 个人认识这两个人。 则满足上述条件的子集最多能有 个?
2.将边长为 n 的正三角形每边 n 等分,过每个分点分别做另外两边的平行线,得到若干个正三角形, 我们称为小三角形。正三角形的一条通路是一条连续的折线,起点是最上面的一个小三角形,终点是最 下面一行位于中间的小三角形。在通路中,只允许由一个小三角形走到另一个与其有公共边的且位于同 一行或下一行的小三角形,并且每个小三角形不能经过两次或两次以上(图中是 n=5 时一条通路的例 子)。设 n=10,则该正三角形的不同的通路的总数为_ __。
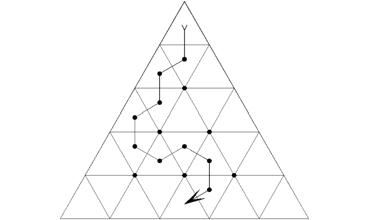
问题解答:
1.思考过程中发现矛盾,若子集只有3人,A认识B,A认识C,B、C互不认识,那A算不算认识该集合中的所有人。
(1)在每个子集中,没有人认识该子集的所有人。该条件有问题。
经思考发现每个子集至少3个人,不代表至少3个人,要满足三个条件,子集肯定超过3人。
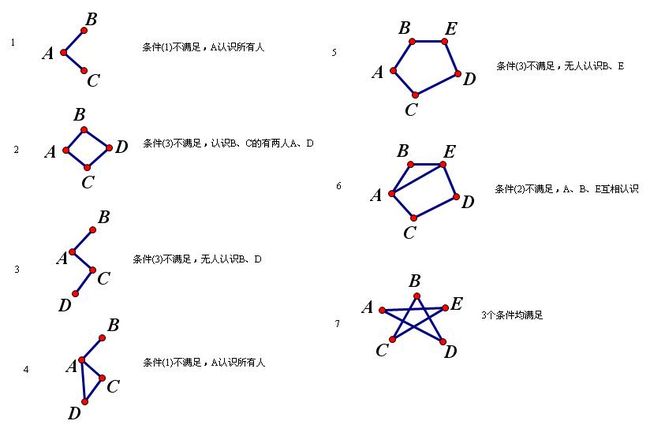
思考过程如上图,1-6都想到了,没有耐心再想下去了,找到http://www.zybang.com/question/7d364e02b9acabe93190e3f1ceb44a2d.html发现基本思路正确,每个子集最少需要5个元素,如上图7所示,离成功之差一步,不过还是很高兴自己能想到1-6.一直在想6个元素怎么构成符合题意的子集。http://tieba.baidu.com/p/143515702提到:
他问的是最多能找出几个集合~
最后剩余的那1个人不算……
多体会体会题目意思,会有帮助的~
本题答案:2006/5=401
2.

方法一:
n=1 0条路径 (1-1)!
n=2 1条路径 (2-1)!
n=3 2条路径 (3-1)!
n=4 6条路径 (4-1)!
猜
n=10 (10-1)!条路径。
方法二:
来自http://tieba.baidu.com/p/2692128895
上层下到下层的第一个点。。然后你就发现。。。这些点通向中间那个终点的路只有一条。。。而上层到下层的第一个到达点的个数是(N-1)所以答案就是(n-1)!
解释:n=4 第1层到第2层有1个路径,第2层到第3层有2个路径,第3层到第4层有3个路径,故总路径为1*2*3=6。
推广到n层,(n-1)!个路径。
1.集合、图 2.排列组合
2.第十三届(NOIP2007)
问题:
1.给定n个有标号的球,标号依次为1,2,…,n。将这n个球放入r个相同的盒子里,不允许有空盒,其不同放置方法的总数记为S(n,r)。例如,S(4,2)=7,这7种不同的放置方法依次为{(1) , (234)} , {(2) , (134)} , {(3) , (124)} , {(4) , (123)} ,{(12) , (34)} , {(13) , (24)} , {(14) , (23)}。当n=7,r=4时,S(7,4)= 。
2.N个人在操场里围成一圈,将这N个人按顺时针方向从1到N编号,然后从第一个人起,每隔一个人让下一个人离开操场,显然,第一轮过后,具有偶数编号的人都离开了操场。依次做下去,直到操场只剩下一个人,记这个人的编号为J(N),例如,J(5)=3,J(10)=5,等等。
则J(400)= 。
(提示:对N=2m+r进行分析,其中0≤r<2m)。
问题解答:
1.
4个盒子,放入球个数如下:
1 1 1 4
1 1 2 3
1 1 3 2(重复)
1 1 4 1(重复)
1 2 1 3(重复)
1 2 2 2
1 2 3 1(重复)
1 3 1 2(重复)
1 3 2 1(重复)
1 4 1 1(重复)
有效个数只有上述三种:1 1 1 4;1 1 2 3;1 2 2 2.
用枚举法得出1 1 1 4有35种
后参考http://www.zybang.com/question/67df89c725b679eedcfa84345b27d353.html
发现1 1 1 4办法C(7,4)=35种。受到启发:1 1 1 4办法C(7,1)*C(6,1)*C(5,1)/P(3,3)=35种
1 1 2 3办法C(7,2)*C(5,3)=210种。或1 1 2 3办法C(7,1)*C(6,1)/P(2,2)*C(5,2)=210中。
1 2 2 2办法C(7,2)*C(5,2)*C(3,2)/P(3,3)=105种。
答案:35+210+105=350
2.
方法一:
已开始准备J(1),J(2),J(3),J(4),......找规律,找着找着,果断放弃。
方法二:
直接处理J(400),第一轮结束:剩奇数200个:1 3 5 7 ......399
第二轮结束剩100个数据:1 5(1+4) 9(5+4) 13(9+4) ...397(393+4)
第三轮结束剩50个数据:1 9(1+8) 17(9+8)......393
第四轮结束剩25个数据:1 17(1+16) 33(17+16)......385
因该轮剩奇数个数据,故,开始手动处理:
1 17 33 49 65 81 97 113 129 145161 177 193 209 225 241 257 273 289 305 321 337 353 369 385
第五轮结束剩:
385 1 33 65 97 129 161 193 225 257 289 321 353
第六轮结束剩:
353 385 33 97 161 225 289
第七轮结束剩:
289 353 33 161
第八轮结束剩:
289 353 33 161
第九轮结束剩:
28933
第十轮结束剩:
289
答案:289
本题虽然方法二也不慢,但实际操作过程中,还是容易出错。
有无通法:https://zhidao.baidu.com/question/582894513179510725.html
289人
把N写成2的K次方加X的形式
则J[N]=2X+1
400=2的8次方加144
所以是第2*144+1=289个人
3.第十四届(NOIP2008)
问题:
1.有6个城市,任何两个城市之间有一条道路连接,6个城市之间两两之间的距离如下表表示,则城市1到城市6的最短距离为____________。
| |
城市1 |
城市2 |
城市3 |
城市4 |
城市5 |
城市6 |
| 城市1 |
0 |
2 |
3 |
1 |
12 |
15 |
| 城市2 |
2 |
0 |
2 |
5 |
3 |
12 |
| 城市3 |
3 |
2 |
0 |
3 |
6 |
5 |
| 城市4 |
1 |
5 |
3 |
0 |
7 |
9 |
| 城市5 |
12 |
3 |
6 |
7 |
0 |
2 |
| 城市6 |
15 |
12 |
5 |
9 |
2 |
0 |
2.书架上有21本书,编号从1到21 从中选4本,其中每两本的编号都不相邻的选法一共有___________________种。
问题解答:
1.
迪杰斯特拉算法:
0 2 3 1 12 15 (1)
0 2 3 1 8 10 (2)
0 2 3 1 5 10 (3)
0 2 3 1 5 8 (5)
0 2 3 1 5 7 (7)
答案:7
2.
想破头,结果一看http://www.zybang.com/question/98ecde8191580f87432df06e7153dcb4.html还挺简单,不过层层剥离,想到这个层面,确实挺难。
假如书架上现已放好了17本书,现要将4本书插入进去且使之任意两本不相邻,即在18个空中插入4本书,列式为:C(18,4)=3060
4.第十五届(NOIP2009)
问题:
1.拓扑排序是指将有向无环图G中的所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若 ∈E(G),则u在线性序列中出现在v之前,这样的线性序列成为拓扑序列。如下的有向无环图,对其顶点做拓扑排序,则所有可能的拓扑序列的个数为 。

2.某个国家的钱币面值有1, 7, 72,73共计四种,如果要用现金付清10015元的货物,假设买卖双方各种钱币的数量无限且允许找零,那么交易过程中至少需要流通 张钱币。
问题解答:
1.题目没看懂,什么是拓扑排序,按着理解做一遍,是一个很小的答案,明显理解有问题。
查了http://www.cnblogs.com/dolphin0520/archive/2011/04/16/2017737.html发现理解没有问题。
通过http://blog.sina.com.cn/s/blog_477c8fd70100h3w7.html对该题有了更深的了解,同时也加深了对拓扑排序的理解。
12376,插入4可以在7前或7后2个位置;123476,123746在1后空位插入5,有6个位置;将89整体插入1237465有8个位置,或者在8个位置中,挑出2个位置插入8,9。故个数为:
2*6*(8+C(8,2))=2*6*(8+28)=432个。
2.进制装换及允许找零
10015=4*7^4+1*7^3+1*7^2+2*7^1+5*7^0
4*7^4=28*7^3
5*7^0=1*7^1-2*7^0
共纸币张数:28+1+1+2+1+2=35张
1.拓扑排序,排列组合 2.进制转换
2016-12-7 20:06



