通俗解释matlab之模拟退火求TSP问题（一）

1.初识模拟退火算法

        说起模拟退火算法，不管哪个地方讲反正都有那么一段历史来源，模拟退火据说就是根据物理学上物质分子在温度较高的时候运动剧烈，很容易从一个转台转到另一个状态，而在温度较低的时候运动缓慢，状态也就基本上固定而不宜发生转变。明不明白这个具体的物理过程无所谓，理解后面算法流程后就明白了什么是退火降温。说白了，如果和算法结合起来的话，就是高温的时候问题的解很容易发生改变，从一个解很容易变化到另外的一个解，随着温度的降低，解的这种改变性越来越低。而在每一次降温的过程中，算法都会记录上在本次温度下的所有改变的解中的优秀解，并传递到下一次的降温过程中。这样，你想一想，开始解的变化范围很大，并一直在寻找优解，慢慢的变化范围变小，就变成了锁定前一次寻找到的最优解。其实基本上所有的算法都是这样的一个过程，先广度搜索，在集中寻找等等，不同的是不同的算法他们的搜索速度、搜索的准确率不同而已。

2.我要解决的问题

既然是优化算法，那就用它来解决一个常见的问题---旅行商问题，也叫TSP问题。问题是什么样子的呢，就是随机给你不同的地点，要你每个地点走一次的话，怎么走这个地点的顺序才能使得你走的总路程最短呢，像这类问题最好的验证实例就是邮递员了吧，他会想怎么邮递所有的包裹才能使得他要走的总路线最少吧。好了下面我随便给出30个不同的点代表不同的位置吧，点的左边都在0~1之间，如下：

cities1=[0.6606,0.9695,0.5906,0.2124,0.0398,0.1367,0.9536,0.6091,0.8767,0.8148,0.3876,0.7041,0.0213,0.3429,0.7471,0.4606,0.7695,0.5006,0.3124,0.0098,0.3637,0.5336,0.2091,0.4767,0.4148,0.5876,0.6041,0.3213,0.6429,0.7471;

0.9500,0.6740,0.5029,0.8274,0.9697,0.5979,0.2184,0.7148,0.2395,0.2867,0.8200,0.3296,0.1649,0.3025,0.8192,0.6500,0.7420,0.0229,0.7274,0.4697,0.0979,0.2684,0.7948,0.4395,0.8867,0.3200,0.5296,0.3649,0.7025,0.9192];

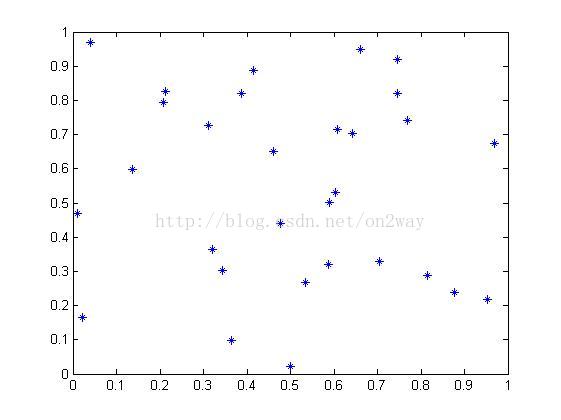
注意了，这就是30对（x,y）的值，在matlab下画出来就如图所示：

plot(cities1(1,:),cities1(2,:),'*')

 

现在问题就是怎么首尾相连这些点才能是他们点之间的距离最小。

（3）关于如何开展算法

地点知道了那么剩下的就是如何开始了。首先最关键的就是点的顺序问题。上面我们给了一系列点，我们的假设就是那些点的先后顺序就是我们要走的顺序，而算法的开展就是改变那些点的循序。比如说上面的点中，第一个点是（0.6606,0.6606），第五个点是（0.0398,0.0398）吧，其他的类似就不说了，那么开始走的顺序就是从第一个点走到第二个点，然后再到第三个点，等等。好了，那么如果我把第一、五的位置换一下，现在第一个要走的点是（0.0398,0.0398），第五个要走的点就是（0.0398,0.0398），其他都先不变的话，那么你想想没变化前你从一点走到二点的距离和变化后你从一点走到二点的距离一样吗？显然不一样。那么好了，不一样就会有大小吧，记录所有距离和的较小者，ok了。并且这种交换可不是只有两个两个交换呀，可以多个相互交换。并且可以交换多次，这样可以产生多少组不同的走法呀，里面不乏有更好的解吧。讲到这里我们也就清楚了我们有哪些事情要干了吧，首先，得有一个负责交换点的函数吧，换完后，肯定还的有一个针对这种顺序下求他们的相互顺序点点之间所有距离和的函数吧。还有一个就是模拟退火的精髓函数，它是决定着某次交换操作后根据所得的结果来决定是否接受本次交换的函数。

针对模拟退火的这个精髓函数，其实它的最基本的原则就只有一个，就是如果交换后距离变小了，那么一定接受这个交换结果，（重点来了）如果交换后距离变大了，那么它不是立马就拒绝这个结果，而是以一定的概率接受这个结果，这个概率的计算方法是 p=exp[-(Ej-Ei)/T],其中Ej相当于交换后的距离值，Ei相当于交换前的距离值，而T就是我们所说的温度了，那么我们说当Ej>Ei时，是不是以这个概率p接受这个解呀，想想，此时的(Ej-Ei)是不是一个小的正值呀（相当于误差），而T温度，肯定也是一个正值，只不过在迭代的过程中我们在一直减小这个T值，所以叫降温嘛。好了我们来看看这个p值怎么变化的吧，再想想，我们说开始的时候高温，也就是T很大是不是，那么exp[-(Ej-Ei)/T]想想大概是多少，假设(Ej-Ei)也就是误差波动不大的话，是不是应为T很大导致-(Ej-Ei)/T从负向趋近于0呀，那么exp[-(Ej-Ei)/T]趋近于1是吧（exp函数性质，不懂的话就没办法了），也就是这个概率p趋近于1，什么概念呀，是不是基本上温度T高的时候，即使碰到了交换后不好的结果也接受呀。好了，再想想，随着T迭代慢慢的下降，T作为分母是不是使得整个P值在慢慢下降呀，也就是接受坏的结果的概率慢慢下降，到最后当T下降到很小的时候，-(Ej-Ei)/T是不是就负向很大了呀，那么p=-(Ej-Ei)/T基本上趋近于0了，也就是再碰到坏的解就基本上不接受了吧。理解了这个精髓部分，这个算法基本上差不多了，剩下的就是发挥部分了，怎么去选择初始温度呀，迭代次数是多少合适呀，每次交换几个点的位置比较好呀，再有就是如何降温，是以一定的比例降温还是怎么降温呀，这一切一切都决定着你的算法是否能很好的找到最优解。下面来实践吧；

（4）输入初始数据到matlab

      function d = datafile1()    %初始城市距离

cities1 = [0.6606,0.9695,0.5906,0.2124,0.0398,0.1367,0.9536,0.6091,0.8767,...  

 0.8148,0.3876,0.7041,0.0213,0.3429,0.7471,0.4606,0.7695,0.5006,0.3124,0.0098,0.3637,0.5336,0.2091,0.4767,...

0.4148,0.5876,0.6041,0.3213,0.6429,0.7471;0.9500,0.6740,0.5029,...

0.8274,0.9697,0.5979,0.2184,0.7148,0.2395,...

0.2867,0.8200,0.3296,0.1649,0.3025,0.8192,0.6500,0.7420,0.0229,...

0.7274,0.4697,0.0979,0.2684,0.7948,0.4395,...

0.8867,0.3200,0.5296,0.3649,0.7025,0.9192];

save cities1.mat cities1;  

像这样建一个m文件，用的时候运行一下它，会生成mat文件，点击既可以把这个矩阵导到matlab工作框中了，这样做也便于修改。当然你也可以直接输入这个矩阵，不过很麻烦，数据量大的话怎么输入。

（5）关于如何交换地点

有了上面理论说明，下面直接程序吧：

%-------------函数说明----------------

%    交换地点顺序

%       输入变量：

%               inputcities:原来的地点顺序和位置

%                    n：    要交换的次数（即多少对地点相交换）

%       输出变量：

%               s：交换后的地点顺序和位置

%---------------------------------------

function s = swapcities(inputcities,n) 

s = inputcities;

 for i = 1 : n

city_1 = round(length(inputcities)*rand(1));%生成随机交换点（1~30之间

%吧）round 四舍五入                         

    if city_1 < 1      %小于1取1，最小不也就是1吗

        city_1 = 1;

    end

    city_2 = round(length(inputcities)*rand(1));

    if city_2 < 1

        city_2 = 1;

    end

    temp = s(:,city_1);        %交换操作，c语言中不经常这么替换吗

    s(:,city_1) = s(:,city_2);

    s(:,city_2) = temp;

end

简单吧，不解释。

（6）关于计算一定顺序的距离和

%-------------函数说明----------------

%    距离计算函数

%       输入变量：

%               inputcities:原来的地点顺序和位置

%       输出变量：

%               d：顺序相加的距离和

%---------------------------------------

function d = distance(inputcities)   %城市距离求和

d=0;

for n = 1:length(inputcities)

   if n == length(inputcities)   %首尾的距离计算

        d = d + norm(inputcities(:,n) - inputcities(:,1));

    else 

        d = d + norm(inputcities(:,n) - inputcities(:,n+1)); %相邻两个点的距离   

    end 

end

对其中norm解释一下，norm是一个求范数的操作，范数某种意义上就是长度、大小、距离的意思，在这里看看，norm里面是不是x和y的坐标差呀，这样算后就是这两个点之间的距离，不明白的就可以认为是对坐标差的（x^2+y^2）开方，勾股定理明白吧，就是它了，比如norm（3,4）=norm（4,3）=norm（-3,4）=norm（-4,-3），是多少，都是5，这就是范数。

其他好理解吧。

（7）最精髓的部分，关于降温选择

%-------------函数说明----------------

%    模拟退火函数

%       输入变量：

%               inputcities:原来的地点顺序和位置

%       initial_temperature：初始温度

%              cooling_rate： 降温比例系数

%               threshold  ： 一个循环次数

%     numberofcitiestoswap ： 每次交换地点的对数  

%---------------------------------------

function  simulatedannealing(inputcities,initial_temperature,...

    cooling_rate,threshold,numberofcitiestoswap)             %退火算法

tempeature = initial_temperature;       %初始温度

input_cities = inputcities;             %城市坐标

 plot(input_cities(1,:),input_cities(2,:),'*');  

 %画出开始图像，与后面对比

 hold on,plot(input_cities(1,:),input_cities(2,:));

 figure;

while tempeature > 0.01         %循环条件，把降温底线作为条件         

    for i = 1 : threshold               %循环次数

       previous_distance = distance(input_cities); %旧距离和

       temp_cities = swapcities(input_cities,numberofcitiestoswap);  

%随机n次交换

       current_distance = distance(temp_cities);   %新距离和

       diff = abs(current_distance - previous_distance);  %产生误差

       if current_distance < previous_distance     

%距离变少了，直接接受，不用考虑 

           input_cities = temp_cities;             %接受    

       else if rand(1) < exp(-diff/(tempeature))   %否则，以一定的概率接受

               input_cities = temp_cities;        %概率符合了，进来接受       

           end

       end

    end

   tempeature = tempeature*cooling_rate;      %降温过程

end

   fprintf('\t\t\tTempeature = %3.8f\n',tempeature);     %输出结果      

   current_distance = distance(input_cities);

   fprintf('\t\t\tFinal_istance = % 3.8f\n',current_distance); 

   plot(input_cities(1,:),input_cities(2,:),'*');

   hold on,plot(input_cities(1,:),input_cities(2,:));

 

好了，把上面几个函数编写完成，在运行simulatedannealing函数就有结果了，当然里面的参数的设置好了。对于上面的这个大函数，都有注释，感觉也很简单清晰吧，就不解释了。下面是我的实验结果，当编写完成以后，给相应的参数（自己慢慢试的）：

simulatedannealing(cities1,0.5,0.92,100,1)    

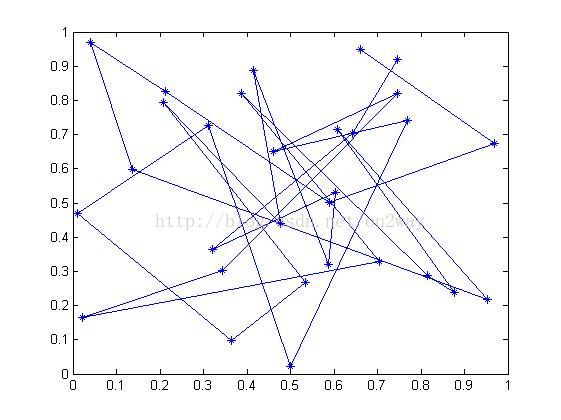
前提是你得把cities1成功输入到matlab中，运行结果如下：

 

这是最初的那个行走路线，看看多差，相互交了多少次。。。

 

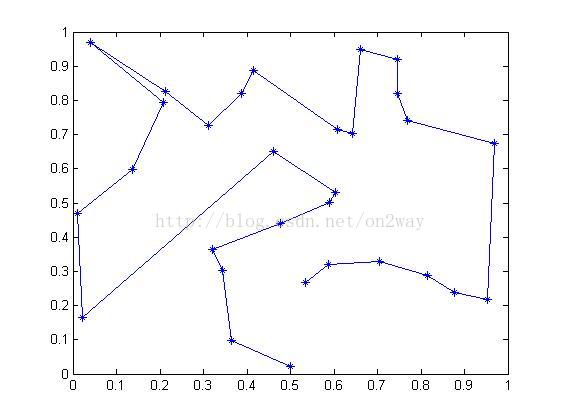
Tempeature = 0.00993111

Final_istance =  5.29570947

这是我的某次运行出来的结果图，可以看到总的行走距离为5.29570947，当然这是我运行了好多回，并且不断调整simulatedannealing里面的参数来的比较好的一个结果，每次的结果还都不一样，大致都在5~8之间，并且我感觉这肯定不是最优解，最优解应该比这个还小才对。不过这是最基础的算法了，没有一点改进，比如说降温率固定了，循环次数固定了，每次交换对数固定了等等，能达到这个效果还行吧。如果再好好对这个算法进行改善下，比如说把这些固定的值改为动态改变的话，效果肯定会好些，具体怎么改善算法，可以去看相关专业文献，明白了模拟退火的基本原理再去改善就很好理解了。下回合再来发个改善版的算法吧，看看效果能优化到哪里吧。

改进的模拟退火求TSP问题（二）