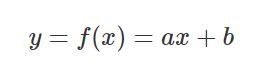逻辑回归和线性回归,代价函数,交叉熵函数,极大似然估计

 

目录
1. 什么是逻辑回归？

3.逻辑回归和线性回归关系

3. 最大似然估计->代价函数

---

1. 什么是逻辑回归？

在线性回归模型中，输出一般是连续的，例如

模型的定义域和值域都可以是[-∞, +∞]。

逻辑回归:输入可以是连续的[-∞, +∞]，但输出一般是离散的，即只有有限多个输出值。例如，其值域可以只有两个值{0, 1}，这两个值可以表示对样本的某种分类，高/低、患病/健康、阴性/阳性等，这就是最常见的二分类逻辑回归。\

3.逻辑回归和线性回归关系

按下图的理解:逻辑回归=线性回归函数+Sigmoid函数

3. 最大似然估计->代价函数

(对数似然估计,对数损失函数,极大似然估计,对数损失, 即对数似然损失(Log-likelihood Loss), 也称逻辑斯谛回归损失(Logistic Loss)或交叉熵损失(cross-entropy Loss), 是在概率估计上定义的.它常用于(multi-nominal, 多项)逻辑斯谛回归和神经网络,以及一些期望极大算法的变体. 可用于评估分类器的概率输出.)

        此时我们想要找到一组w,使函数正确的概率最大.而我们在上面的推理过程中已经得到每个单条样本预测正确概率的公式:

                P(正确) = * 

最后得到代价函数,

逻辑回归一般使用交叉熵作为代价函数。关于代价函数的具体细节，请参考代价函数，这里只给出交叉熵公式：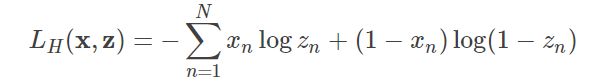

这个对数损失函数与上面的极大似然估计的对数似然函数本质上是等价的。所以逻辑回归直接采用对数损失函数来求参数，实际上与采用极大似然估计来求参数是一致的。（损失函数的目标是最小化，似然函数则是最大化，二者仅相差一个符号）。

 

reference:
https://blog.csdn.net/saltriver/article/details/63683092

https://www.cnblogs.com/stAr-1/p/9020537.html

https://blog.csdn.net/lanchunhui/article/details/75433608