目标检测Anchor free方法总结：YOLOv1、CornerNet、CenterNet、FCOS

YOLOv1（2016）:https://arxiv.org/pdf/1506.02640.pdf
CornerNet（2018）:https://arxiv.org/pdf/1808.01244.pdf
CenterNet（2019）:https://arxiv.org/pdf/1904.08189.pdf
FCOS（2019）：https://arxiv.org/pdf/1904.01355.pdf

什么是Anchor free方法？

  Anchor free是相对于Anchor base而言的一种目标检测方法，anchor base需要在图像的特征图中每个位置预先设置一定数量的anchor，然后对每个anchor进行分类和回归。而anchor free的方法则不需要预先设定anchor，直接对图像进行目标检测。anchor free的方法相对于anchor base有几个好处：
  1、不用设计关于anchor的超参数如anchor的数量、边长、长宽比、IOU阈值等，而这些超参数在anchor base方法中对网络性能影响很大。
  2、训练过程中不用重复计算大量的IOU。在anchor base中假如在一个30*30的feature map中每个位置有9个anchor，那么对于每一个真实目标框要计算30*30*9=8100次IOU来筛选正样本。对于多级多目标预测计算量大大增加。
  3、在anchor base方法中需要预设大量的anchor，如果不使用RPN网络筛选建议框，那么训练会存在大量的负样本，而添加RPN网络会降低网络的推理速度，anchor free则不存在正负样本不均衡的问题。

YOLOv1

  网络结构

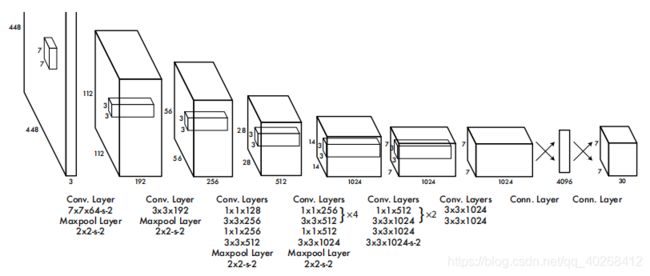
  网络由24卷积层和2个全连接层顺序叠加组成。

  实现方法
  通过卷积网络进行特征提取，生成S×S的feature maps（图中为7×7），特征图上的每个点映射在原图上为一个方格，那么原图上就是S×S的网格。对于一个真实的目标框其中心点落在那个网格内，那么那个网格就负责预测这个目标。每个网格要预测B个bounding box，每个bounding box除了要回归自身的位置（x，y，w，h）之外，还要附带预测一个confidence值，其中x，y是边界框相对于其所在单元格的偏移（一般是相对于单元格左上角坐标点的偏移，在这里每个正方形单元格的边长视为1，故x，y在[0,1]之间）；w，h分别是预测的边界框宽，高相对于整张图片宽，高的比例，也是在[0,1]之间。原始网络是预测2个bbox，所以上图网络最后输出就是7×7×（20+2×（1+4）），20为类别数。网络预测后的bbox通过NMS进行过滤，得到最终的检测框。
  损失函数如下图所示：

  前两项是bbox位置误差项，然后两项是bbox置信度误差项，最后一项是包含目标的单元格分类误差项。

  YOLOv1是对S×S个网格直接预测B个bbox（x，y，w，h，c），而没有预先设定anchor，它也是第一个anchor free的目标检测算法，而在后来的YOLOv2中则采用了anchor机制来提高算法召回率。

CornerNet

  网络结构

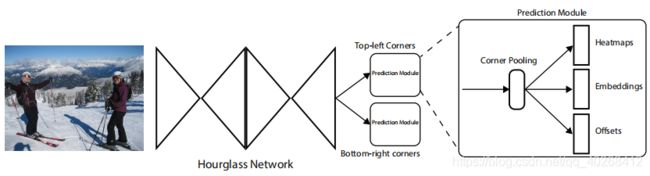
  网络的backbone采用沙漏网络，具体结构参考：Hourglass。然后对主干网络进行两个分支预测：一个分支是对bbox左上角的角点进行预测，另一个分支则是对bbox右下角的角点进行预测。在每个分支中首先进行corner pooling，然后生成三个分支Heatmaps、Embeddings、Offsets。

  Corner Pooling
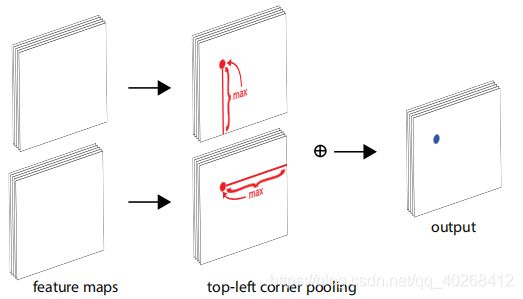
  在对目标左上角进行检测时，由先验知识可以知道，目标的信息包含在该点的右下方，因此作者设计了Corner Pooling来融合某点轴线方向上的信息，top-left corner pooling如下图所示：

  top-left corner pooling是分别将目标点垂直轴线以下的位置提取最大值，然后对水平轴线以右的位置提取最大值，将两个最大值相加即为该点池化后的结果，实际应用时可以从右向左、从下向上进行更新计算，减小复杂度，提高计算效率，实例计算如下所示。bottom-right corner pooling原理类似。

  Heatmaps
  Heatmaps的作用是预测某一点是否为某个目标的角点。以左上角分支为例，网络预测的Heatmaps为H×W×C，C为类别数，每个channel为一个二值量，全为负数时表示该点预测为背景。另外在训练计算损失函数时，作者只将ground truth角点处的点划为正样本，但是因为在真实角点附近的负样本也可以得到较大重叠区域的bbox，因此作者在计算这些邻近负样本的损失函数时运用一个二维高斯函数进行约束，$x,y$为点$(i,j)$离真实点的距离，论文中$\delta$取1/3$r$：
$$y_{cij}=\{\begin{array}{llc}{e}^{-\frac{x^2+y^2}{2{\delta }^2}}& x^2+y^2\le r^2& \\ 0& else& \end{array}$$
  Heatmaps部分损失函数使用Focal loss：
$$L_{det}=-\frac{1}{N}\sum _{c=1}^C\sum _{i=1}^H\sum _{j=1}^W\{\begin{array}{llc}(1-p_{cij}{)}^{\alpha }log(p_{cij})& y_{cij}=1& \\ (1-y_{cij}{)}^{\beta }(p_{cij}{)}^{\alpha }log(1-p_{cij})& else& \end{array}$$
  N为整张图片中目标数量，$\alpha ,\beta$为控制权重的超参数，文章中分别取2和4。由损失函数可以看出，通过高斯函数的约束，即使把离真实点很近的点预测为目标点，其损失函数会很低，近似可以认为是预测正确的。

  Offset
  假设网络的下采样率为n，那么在输入图像上的点$(x,y)$映射在Heatmaps上为$(\lfloor \frac{x}{n}\rfloor ,\lfloor \frac{y}{n}\rfloor )$，存在精度丢失的情况。设与第$k$个真实框的坐标偏差为:
$$o_k=(\frac{x_k}{n}-\lfloor \frac{x_k}{n}\rfloor ,\frac{y_k}{n}-\lfloor \frac{y_k}{n}\rfloor )$$
  Offset的作用就是对目标位置的偏差进行回归预测，损失函数可以表示为：
$$L_{off}=\frac{1}{N}\sum _{k=1}^N\sum _{i\in \{x,y\}}SmoothL1Loss(o_k^i,{\hat{o}}_k^i)$$
  以上损失函数只对真实目标角点位置进行计算

  Embedding
  对角点进行了预测和修正，由于对左上角点和右下角点是分开进行预测，那么需要对真实目标的左上角点和右下角点进行匹配以获得最后的目标框。Embedding的作用就是对每个点预测一个嵌入向量，将左上角分支与右下角分支中嵌入向量相似的点进行匹配。Embedding的输出为H×W×L，L为嵌入向量的长度，文中取1。设左上角的嵌入向量为$e_{tk}$，右下角的嵌入向量为$e_{bk}$，那么作者将该部分的损失函数设计为两个部分：
$$L_{pull}=\frac{1}{N}\sum _{k=1}^N[(e_{tk}-e_k{)}^2+(e_{bk}-e_k{)}^2]，e_k=\frac{e_{tk}+e_{bk}}{2}$$
$$L_{push}=\frac{1}{N(N-1)}\sum _{k=1}^N\sum _{j=1,j\ne k}^{N}max(0,\Delta -|e_k-e_j|)$$
公式中$\Delta$取1，从公式可以看出，pull损失函数目的是将属于同一个目标的$e_{tk}$，$e_{bk}$拉的更相似；push损失函数则是将不同目标的$e_k$之间差距拉大。跟offset损失一样，以上两个损失也只对真实的角点位置进行计算。

  网络预测分支的具体结构如下图所示：

CenterNet

  网络结构

  CenterNet与CornerNet的总体思路相似，改进了CornerNet中的corner pooling方式，并增加了一个预测中心点的分支，主干网络也是采用的Hourglass。

  Center pooling & Cascade corner pooling

  center pooling（上图a）的方式与corner pooling（上图b）类似，center pooling是在feature maps上的某点的水平和垂直方向上寻找最大值然后相加的到该点池化后的值。而cascade corner pooling（上图c） 则是先沿边界查找最大值（与corner pooling相同），然后在最大值处向内部寻找最大值，将找到的两个最大值相加得到池化后的结果。由以上原理可知center pooling和cascade corner pooling可以由corner pooling在不同方向上串接实现，如下图所示：

  推理过程
  1、选取top-k个center keypoints和top-k对croners（论文取k=70）。
  2、根据offset将center keypoints和croners对应的bbox映射在输入图像上。
  3、检测bbox的中心区域是否包含center keypoints，并且两者的类别要求一致。
  4、将符合条件的bbox保留，将bbox的得分取三个点（左上、右下、中心点）的均值。

  中心区域计算
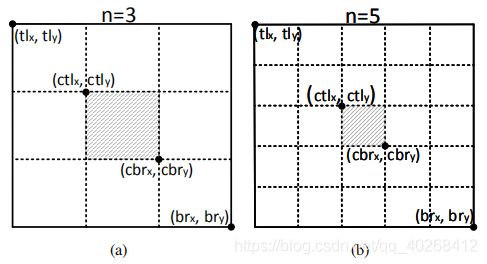
  设bbox左上点的坐标为$(tlx,tly)$，坐下点的坐标为$(brx,bry)$。那么中心区域的四个点的计算方法如下所示：
$$\{\begin{array}{ll}ctlx=\frac{(n+1)tlx+(n-1)brx}{2n}& \\ ctly=\frac{(n+1)tly+(n-1)bry}{2n}& \\ cbrx=\frac{(n-1)tlx+(n+1)brx}{2n}& \\ cbry=\frac{(n-1)tly+(n+1)bry}{2n}& \end{array}$$
  示意图如下所示，论文中bbox边长大于150时取n=5，否则取n=3：

  损失函数
$$L=L_{det}^{co}+L_{det}^{ce}+\alpha L_{pull}^{co}+\beta L_{push}^{co}+\theta (L_{off}^{co}+L_{off}^{ce})$$
其中$L_{det}^{co}$、$L_{pull}^{co}$、$L_{push}^{co}$、$L_{off}^{co}$与CornerNet中定义相同，表示关于corners对的损失函数，另外两项则是关于center的损失函数，同样采用focal loss和l1 loss。

FCOS

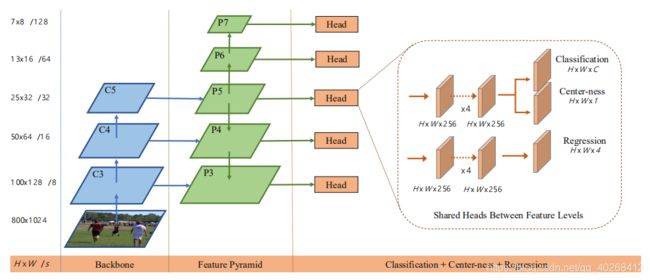
  网络结构

  由图可知，FCOS网络采用金字塔结构对特征进行融合，并在多个特征层进行预测，网络的预测部分有三个分支，在不同特征层$\{P_3,P_4,P_5,P_6,P_7\}$上分别逐点进行类别预测、边界回归、中心度估计，其中$P_6$，$P_7$分别进行了两倍的下采样。FCOS的预测分类策略与YOLOv1有点类似（YOLOv1是在S×S的feature maps上进行分类和预测），可以注意到每个分支的输出都跟feature maps的W×H相同。

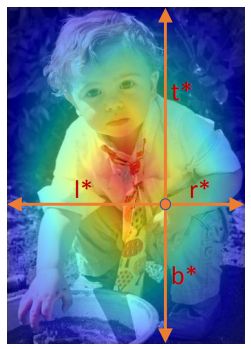
  逐像素回归
  FCOS的回归策略是将feature maps上的点$(x,y)$映射会输入图像上$(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys)$，若映射后的点位于任意一个真实框内则认为其为正样本，将真实框的类别作为该点的类别，并对其边框进行回归$v^{\ast }=(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$，向量中的每个元素表示该点距离bbox四条边的距离，如下图所示。需要注意的是，当映射后的点落在多个真实框内，则认为该点的类别为较小真实框的类别，这种模糊样本可以通过FPN多级预测来进行解决。

  FPN多级预测
  由于存在模糊样本，作者通过限制不同的特征层回归的bbox范围，来消除这种影响。首先在所有特征层上对每个位置计算出回归参数$l^{\ast }$，$t^{\ast }$，$r^{\ast }$，$b^{\ast }$；如果一个位置满足$max(l^{\ast },t^{\ast },r^{\ast },b^{\ast })>m_i或max(l^{\ast },t^{\ast },r^{\ast },b^{\ast })<m_{i-1}$，则把该样本设置为负样本，不再对其进行回归。$m_i$表示第$i$个特征层需要回归的最大距离，论文中$m_2=0,m_3=64,m_4=128,m_5=256,m_6=512,m_7=\infty$。这种策略相当于限制不同级别的feature maps预测不同大小的bbox。

  Center-ness

$$centernes{s}^{\ast }=\sqrt{\frac{min(l^{\ast },r^{\ast })}{max(l^{\ast },r^{\ast })}\times \frac{min(t^{\ast },b^{\ast })}{max(t^{\ast },b^{\ast })}}$$
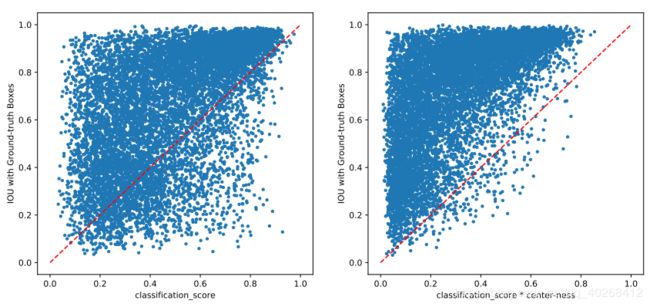
  由公式可以看出，中心度表示预测点在图像中偏离中心的距离，其值在0~1之间，使用二值交叉熵损失进行训练。在进行预测时，bbox最终得分表示为分类置信度和中心度的乘积，这样可以降低那些远离目标中心点的bbox的权重，有利于后续的NMS过滤筛选，可以显著提高网络的性能，并且没有任何超参数。作者在论文中提到可以提前限制位于目标中心的点为正样本（类似于CenterNet的中心区域？），来替代中心度的方法，但是这样会有一个超参数。下图是有无中心度的效果：

以后若有效果比较好的anchor free网络，本博客会持续更新。

以上。