从 one-hot 到 softmax,再到交叉熵,技术一脉相承
1. one-hot 编码的来源
神经网络实际上可以看作传统逻辑电路的推广。逻辑电路里面的信号只有0,1两个结果,而神经网络里面的信号,利用 sigmoid 函数强制变换到 (0,1) 区间。
神经网络的二分类模型,第一层的每个神经元,都可以生成一个空间线性分割的判别式,经过 sigmoid 函数激活,变换到 (0,1) 区间。因此,第一层输出的 n 个节点,表示输入向量分别落入 n 个分割平面的哪一侧。
从第二层开始,输入节点的值都是一个“模糊”布尔值,取值范围在(0,1)区间。然后第二层和第三层对这些输入变量做 and 和 or 这两个逻辑运算。借助 sigmoid 函数,and 运算和 or 运算可以表示成统一的形式。
x 1 ∧ x 2 = σ ( x 1 + x 2 − 1.5 ) x 1 ∨ x 2 = σ ( x 1 + x 2 − 0.5 ) (1) \tag1 \begin{matrix} x_1 \land x_2 = \sigma(x_1 + x_2 - 1.5)\\ x_1 \lor x_2 = \sigma(x_1 + x_2 - 0.5)\\ \end{matrix} x1∧x2=σ(x1+x2−1.5)x1∨x2=σ(x1+x2−0.5)(1)
附注:因为 and 运算和 or 运算可以统一表示成 σ ( x 1 + x 2 − w ) \sigma(x_1+x_2-w) σ(x1+x2−w)
的形式,因此,对应的神经元节点参数可以让训练算法自行决定, w w w 小于 1,就代表 or 运算,否则代表 and 运算。
二分类网络最终输出节点只有一个。要实现 n 分类能力,可以训练 n 个二分类网络,然后合并起来,这样的 n 分类网络具有 n 个输出节点。理想情况下,只有一个节点输出 1, 其他节点都输出 0。这就是所谓的 one-hot 编码。
2. softmax 的来历
事实上,n 分类网络一般不会输出理想的 one-hot 编码,为加快网络输出结果尽快向 one-hot 编码收敛,最后一层的输入节点,应该取消 sigmoid 激活,可以允许最后一层的输入节点值域为 ( − ∞ , + ∞ ) (-\infty,+\infty ) (−∞,+∞)。然后对于最后一层的输入 ( x 1 , x 2 , . . . , x n ) (x_1,x_2,...,x_n) (x1,x2,...,xn) 做如下变换:
y i = e x i e x 1 + e x 2 + . . . + e x n , ( i = 1 , 2 , . . . , n ) (2) \tag2 y_i=\frac{e^{x_i}}{e^{x_1}+e^{x_2}+...+e^{x_n}},(i=1,2,...,n) yi=ex1+ex2+...+exnexi,(i=1,2,...,n)(2)
这个变换称为 softmax 函数,其作用是让 x i x_i xi 中最大的数变得更大,其他的变得更小,而且输出变量 y i y_i yi 的总和恒为 1。
3. 传统损失函数的弊病
假设 y i y_i yi 是训练样本给出的真实结果, F ( x i , w ) F(x_i, w) F(xi,w) 是模型给出的预测结果。容易想到,损失函数可以按照下面方式定义,
L o s s ( w ) = ∑ ∣ F ( x i , w ) − y i ∣ (3) \tag3 Loss(w) = \sum|F(x_i,w)-y_i| Loss(w)=∑∣F(xi,w)−yi∣(3)
损失函数的定义原则是,如果预测结果与是及样本真实结果的距离越远,给予的惩罚就要越大。(3)式非常直观地体现出了这一点。
回归模型输出结果值域通常为 ( − ∞ , + ∞ ) (-\infty,+\infty ) (−∞,+∞),(3) 式效果符合预期。但基于 softmax 的分类网络而言,情况并不理想。以二分类网络为例,输出结果 F ( x i , w ) F(x_i, w) F(xi,w) 与真实结果 y i y_i yi 的最大距离不会超过 1,因此,模型参数 w w w 与理想参数之间差距无限增大,也不会导致输出结果 F ( x i , w ) F(x_i, w) F(xi,w) 与真实结果 y i y_i yi 的距离明显增加。这说明传统基于距离度量的损失函数,用于基于 one-hot 或者 softmax 的分类模型,无法对更差的模型参数给予更大的惩罚。这会严重影响模型训练效果。
4. 交叉熵
对于预测结果和真实结果之间的差,如何设计一个合理的惩罚函数?我们依据真实样本的值分别看一下。
4.1 真实样本 y i = 1 y_i = 1 yi=1
我们希望构造一个函数,符合下面的条件:
L o s s i ( w ) = { 0 , ( F ( x i , w ) = 1 , 预 测 正 确 , 惩 罚 为 零 ) + ∞ , ( F ( x i , w ) = 0 , 预 测 完 全 错 误 , 惩 罚 无 穷 大 ) (4) \tag4 Loss_i(w)= \begin{cases} 0,&&(F(x_i,w)=1,预测正确,惩罚为零)\\ +\infty,&&(F(x_i,w)=0,预测完全错误,惩罚无穷大) \end{cases} Lossi(w)={0,+∞,(F(xi,w)=1,预测正确,惩罚为零)(F(xi,w)=0,预测完全错误,惩罚无穷大)(4)
这个函数不难找,下面是一个简单的方案:
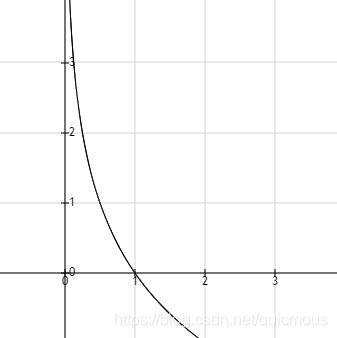
L o s s i ( w ) = − l o g [ F ( x i , w ) ] , ( y i = 1 ) (5) \tag5 Loss_i(w)=-log[F(x_i,w)], \ \ \ \ (y_i=1) Lossi(w)=−log[F(xi,w)], (yi=1)(5)
这个函数很有意思,我期望你输出1,如果你听话,惩罚就是0;如果输出结果 0 这一端靠近,惩罚就趋向无穷大。参见下图,
4.2 真实样本 y i = 0 y_i = 0 yi=0
对于 y i = 0 y_i=0 yi=0 而言,模型应该输出数值0。因此,定义惩罚函数:
L o s s i ( w ) = − l o g [ 1 − F ( x i , w ) ] , ( y i = 0 ) (5) \tag5 Loss_i(w)=-log[1-F(x_i,w)], \ \ \ \ (y_i=0) Lossi(w)=−log[1−F(xi,w)], (yi=0)(5)
这个函数同样有意思,我期望你输出0,如果你听话,惩罚就是0;如果输出结果 向1 这一端靠近,惩罚就趋向无穷大。参见下图,

于是我们得到了下面的惩罚函数:
L o s s i ( w ) = { − l o g [ F ( x i , w ) ] , ( y i = 1 ) − l o g [ 1 − F ( x i , w ) ] , ( y i = 0 ) (6) \tag6 Loss_i(w) = \begin{cases} -log[F(x_i,w)],&&(y_i=1)\\ -log[1-F(x_i,w)],&&(y_i=0) \end{cases} Lossi(w)={−log[F(xi,w)],−log[1−F(xi,w)],(yi=1)(yi=0)(6)
采用个小技巧,合并在一起,
L o s s i ( w ) = − y i l o g [ F ( x i , w ) ] − ( 1 − y i ) l o g [ 1 − F ( x i , w ) ] (7) \tag7 Loss_i(w)=-y_ilog[F(x_i,w)]-(1-y_i)log[1-F(x_i,w)] Lossi(w)=−yilog[F(xi,w)]−(1−yi)log[1−F(xi,w)](7)
公式看上去高大上很多,但这只是雕虫小技而已,你可以分别令 y i = 1 , y i = 0 y_i=1,y_i=0 yi=1,yi=0 带入验证一下,应该和(6)效果一样。
3. 交叉熵损失函数
如果有 N 个训练样本 ( x i , y i ) , i = 1 , 2 , . . . , N (x_i, y_i), i =1,2,...,N (xi,yi),i=1,2,...,N。损失函数可定义为
L o s s ( w ) = ∑ i = 1 N { − y i l o g [ z ( x i , w ) ] − ( 1 − y i ) l o g [ 1 − z ( x i , w ) ] } (8) \tag8 Loss(w) = \sum_{i=1}^N\{ -y_ilog[z(x_i,w)]-(1-y_i)log[1-z(x_i,w)] \} Loss(w)=i=1∑N{−yilog[z(xi,w)]−(1−yi)log[1−z(xi,w)]}(8)
当然依据上述原理,我们还可以构造其他类似的损失函数。但是这个成为了业内受欢迎的表达形式,因为人们发现,上述公式可以借助统计学最大似然估计以及信息论中熵的理论冠冕堂皇地推导出来,实现理想与现实完美的统一。因此,这个函数称为交叉熵损失函数。至于其中复杂的数学推导,我们以后再慢慢讨论。
进一步,如果三分类模型的训练样本为 ( x i , r i , s i , t i ) (x_i, r_i, s_i, t_i) (xi,ri,si,ti),输出节点为 α ( x , w ) , β ( x , w ) , γ ( x , w ) \alpha(x,w),\beta(x,w), \gamma(x,w) α(x,w),β(x,w),γ(x,w),交叉熵可以定义如下:
L o s s i ( w ) = − r i l o g [ α ( x i , w ) ] − s i l o g [ β ( x i , w ) ] − t i l o g [ γ ( x i , w ) ] (9) \tag9 Loss_i(w)=-r_ilog[\alpha(x_i,w)]-s_ilog[\beta(x_i,w)]-t_ilog[\gamma(x_i,w)] Lossi(w)=−rilog[α(xi,w)]−silog[β(xi,w)]−tilog[γ(xi,w)](9)
于是,
L o s s ( w ) = ∑ i = 1 N − r i l o g [ α ( x i , w ) ] − s i l o g [ β ( x i , w ) ] − t i l o g [ γ ( x i , w ) ] (10) \tag{10} Loss(w)=\sum_{i=1}^{N}-r_ilog[\alpha(x_i,w)]-s_ilog[\beta(x_i,w)]-t_ilog[\gamma(x_i,w)] Loss(w)=i=1∑N−rilog[α(xi,w)]−silog[β(xi,w)]−tilog[γ(xi,w)](10)
这个貌似比二分类还容易理解。至于 n 分类模型,公式自己应该会推导了吧?