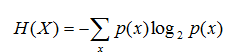信息熵及其Python的实现

一、熵

熵，在信息论中是用来刻画信息混乱程度的一种度量。熵最早源于热力学，后应广泛用于物理、化学、信息论等领域。1850年，德国物理学家鲁道夫·克劳修斯首次提出熵的概念，用来表示任何一种能量在空间中分布的均匀程度。1948年，Shannon在Bell System Technical Journal上发表文章“A Mathematical Theory of Communication”，将信息熵的概念引入信息论中。本文所说的熵就是Shannon熵，即信息熵，解决了对信息的量化度量问题。

信息熵定义如下：

 

其中X为一随机变量，x是该随机变量的可能取值，p(x)是x发生的概率。从定义中可以看出变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。

二、基于Python的信息熵

import math
#以整型数据为例，给出其信息熵的计算程序。
###########################################
'''统计已知数据中的不同数据及其出现次数'''
###########################################
def StatDataInf( data ):
    dataArrayLen = len( data )
    diffData = [];
    diffDataNum = [];
    dataCpy = data;
    for i in range( dataArrayLen ):
        count = 0;
        j = i
        if( dataCpy[j] != '/' ):
            temp = dataCpy[i]
            diffData.append( temp )
            while( j < dataArrayLen ):
                if( dataCpy[j] == temp ):
                    count = count + 1
                    dataCpy[j] = '/'
                j = j + 1
            diffDataNum.append( count )
    return diffData, diffDataNum

###########################################
'''计算已知数据的熵'''
###########################################
def DataEntropy( data, diffData, diffDataNum ):
    dataArrayLen = len( data )
    diffDataArrayLen = len( diffDataNum )
    entropyVal = 0;
    for i in range( diffDataArrayLen ):
        proptyVal = diffDataNum[i] / dataArrayLen
        entropyVal = entropyVal - proptyVal * math.log2( proptyVal )
    return entropyVal

def main():
    data = [1, 2, 1, 2, 1, 2, 1, 2, 1, 2 ]
    [diffData, diffDataNum] = StatDataInf( data )
    entropyVal = DataEntropy( data, diffData, diffDataNum )
    print( entropyVal )
    
    data = [1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1 ]
    [diffData, diffDataNum] = StatDataInf( data )
    entropyVal = DataEntropy( data, diffData, diffDataNum )
    print( entropyVal )
    
    data = [1, 2, 3, 4, 2, 1, 2, 4, 3, 2, 3, 4, 1, 1, 1 ]
    [diffData, diffDataNum] = StatDataInf( data )
    entropyVal = DataEntropy( data, diffData, diffDataNum )
    print( entropyVal )
    
    data = [1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4 ]
    [diffData, diffDataNum] = StatDataInf( data )
    entropyVal = DataEntropy( data, diffData, diffDataNum )
    print( entropyVal )
    data = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 1, 2, 3, 4, 5 ]
    [diffData, diffDataNum] = StatDataInf( data )
    entropyVal = DataEntropy( data, diffData, diffDataNum )
    print( entropyVal )
    
if __name__ == '__main__':
    main()
###########################################
#运行结果
1.0
0.9182958340544896
1.965596230357602
2.0
2.3183692540329317

三、参考文献

1. Shannon C E . The mathematical theory of communication. 1963[J]. Bell Labs Technical Journal, 1950, 3(9):31-32.
2. https://baike.so.com/doc/3291228-3467016.html.

作者：YangYF