连续时间傅里叶变换
1. 非周期信号的表示:连续时间傅里叶变换
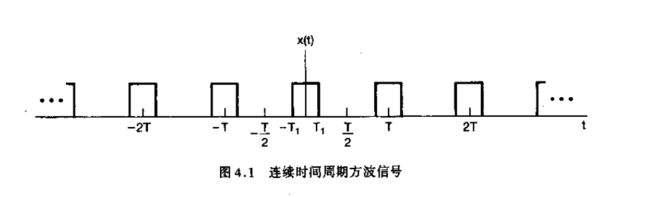
为了对傅里叶变换的实质进行更深入的了解,我们先从一个连续时间周期方波的傅里叶级数表示着手。即,在一个周期内
x ( t ) = { 1 , | t ∣ < T 1 0 , T 1 < ∣ t ∣ < T / 2 x(t) = \begin{cases} 1, & \text |t| < T_1 \\ 0, & \text T_1 < |t| < T/2 \end{cases} x(t)={1,0,|t∣<T1T1<∣t∣<T/2
该方波信号的傅里叶级数系数 a k a_k ak 是
(1) a k = 2 s i n ( k ω 0 T 1 ) k ω 0 T \tag{1}a_k = \frac{2sin(k\omega_0T_1)}{k\omega_0T} ak=kω0T2sin(kω0T1)(1)
式中 ω 0 = 2 π / T \omega_0 = 2\pi/T ω0=2π/T。
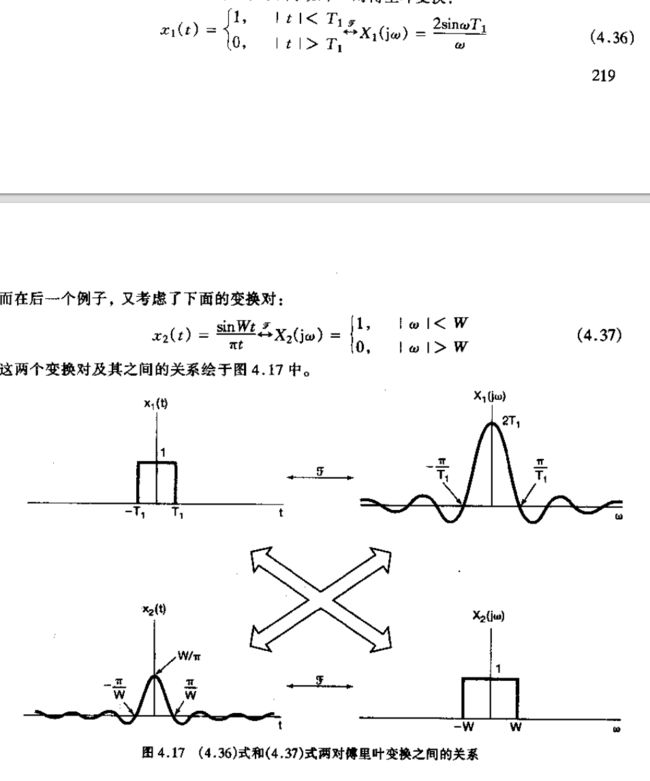
理解(1) 式的另一种方式是把它当作一个包络函数的样本,即
(2) T a k = 2 s i n ω T 1 ω ∣ ω = k ω 0 \tag{2}Ta_k = \frac{2sin\omega T_1}{\omega}\lvert _{\omega=k\omega_0} Tak=ω2sinωT1∣ω=kω0(2)
这就是,若将 ω \omega ω 看作一个连续变量,则函数 $ {(2sin\omega T_1)}/{\omega}$ 就代表 T a k Ta_k Tak 的包络,这些系数就是在此包络上等间隔取得的样本。而且,若 T 1 T_1 T1 固定,则 T a k Ta_k Tak 的包络就与 T T T 无关,如下图所示。
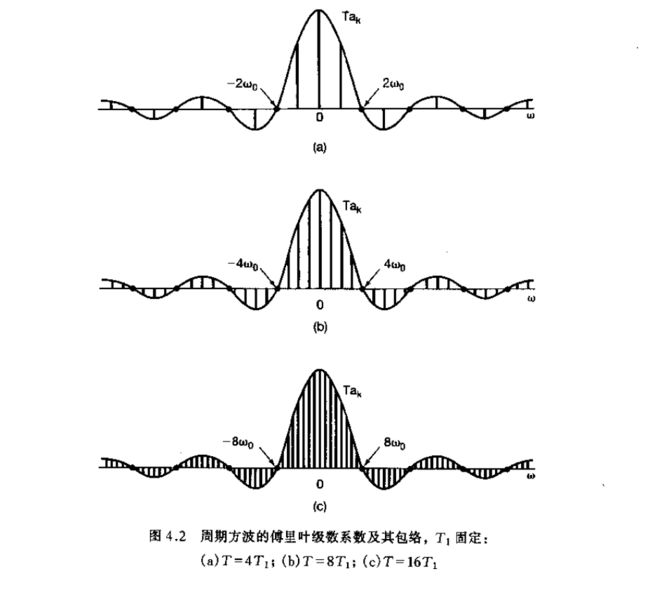
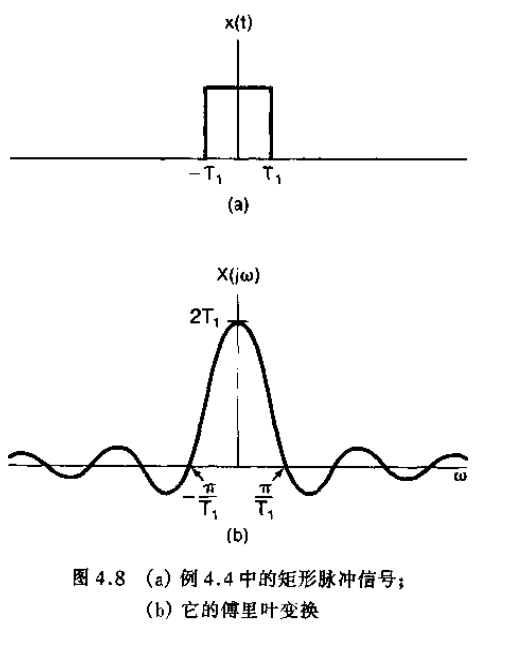
从该图可以看出,随着 T T T 增加,该包络就被以愈来愈密集的间隔采样。随着 T T T 变得任意大,原来的周期方波就趋近于一个矩形脉冲(也就是说,在时域保留下的是一个非周期信号,它对应于原方波的一个周期)。
与此同时,傅里叶级数(乘以 T T T 后)作为包络上的样本也变得愈来愈密集,这从某种意义上来说,随着 T → ∞ T\to \infty T→∞,傅里叶级数就趋近于这个包络函数。
这个例子说明了对非周期信号建立傅里叶表示的基本思想,可以把非周期信号当作一个周期任意大的极限来看待。
现在我们来考虑一个信号 x ( t ) x(t) x(t),它具有有限持续期 2 T 1 2T_1 2T1,从这个周期信号出发,可以构成一个周期信号 x ~ ( t ) \tilde x(t) x~(t),使 x ( t ) x(t) x(t) 就是 x ~ ( t ) \tilde x(t) x~(t) 的一个周期。当把 T T T 选的比较大时, x ( t ) x(t) x(t) 就在一个更长的时段上与 x ~ ( t ) \tilde x(t) x~(t) 相一致,并且随着 T → ∞ T\to \infty T→∞,对任意有限时间值 t t t 而言, x ~ ( t ) \tilde x(t) x~(t) 就等于 x ( t ) x(t) x(t)。
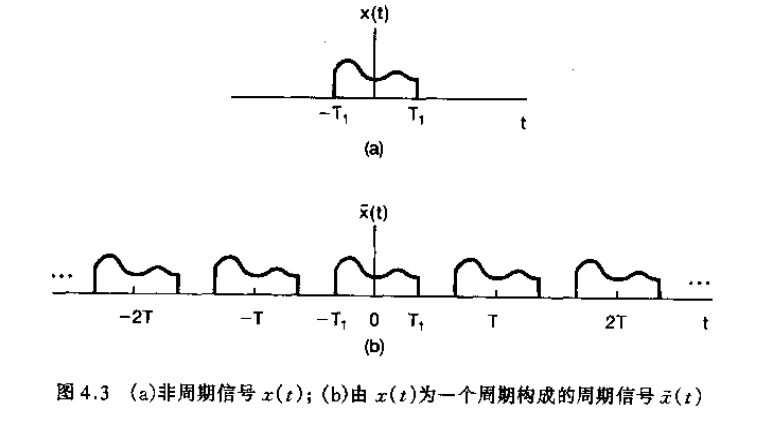
在这种情况下,我们考虑将 x ~ ( t ) \tilde x(t) x~(t) 表示成傅里叶级数,将积分区间选为 − T / 2 ⩽ t ⩽ T / 2 -T/2 \leqslant t \leqslant T/2 −T/2⩽t⩽T/2。
(3) x ~ ( t ) = ∑ k = − ∞ + ∞ a k e j k ω 0 t \tag{3}\tilde x(t) = \sum_{k=-\infty}^{+\infty}a_ke^{jk\omega_0t} x~(t)=k=−∞∑+∞akejkω0t(3)
(4) a k = 1 T ∫ − T 2 T 2 x ~ ( t ) e − j k ω 0 t d t \tag{4}a_k = \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\tilde x(t)e^{-jk\omega_0t}dt ak=T1∫−2T2Tx~(t)e−jkω0tdt(4)
式中 ω 0 = 2 π / T \omega_0=2\pi / T ω0=2π/T,由于在 ∣ t ∣ < T / 2 |t|< T/2 ∣t∣<T/2 内, x ~ ( t ) = x ( t ) \tilde x(t)=x(t) x~(t)=x(t),而在其余地方, x ( t ) = 0 x(t)=0 x(t)=0,所以(4)式可以重新写为
(5) a k = 1 T ∫ − T 2 T 2 x ( t ) e − j k ω 0 t d t = 1 T ∫ − ∞ + ∞ x ( t ) e − j k ω 0 t d t \tag{5}a_k = \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}x(t)e^{-jk\omega_0t}dt=\frac{1}{T}\int_{-\infty}^{+\infty}x(t)e^{-jk\omega_0t}dt ak=T1∫−2T2Tx(t)e−jkω0tdt=T1∫−∞+∞x(t)e−jkω0tdt(5)
因此,定义 T a k Ta_k Tak 的包络 X ( j ω ) X(j\omega) X(jω) 为
(6) X ( j ω ) = ∫ − ∞ + ∞ x ( t ) e − j ω t d t \tag{6}X(j\omega)=\int_{-\infty}^{+\infty}x(t)e^{-j\omega t}dt X(jω)=∫−∞+∞x(t)e−jωtdt(6)
这时候,系数 a k a_k ak 可以写为
(7) a k = 1 T X ( j k ω 0 ) \tag{7}a_k = \frac{1}{T}X(jk\omega_0) ak=T1X(jkω0)(7)
将(3) 和 (7)结合在一起, x ~ ( t ) \tilde x(t) x~(t) 就可以用表示为
(8) x ~ ( t ) = ∑ k = − ∞ + ∞ 1 T X ( j k ω 0 ) e j k ω 0 t = 1 2 π ∑ k = − ∞ + ∞ X ( j k ω 0 ) e j k ω 0 t ω 0 \tag{8}\tilde x(t) = \sum_{k=-\infty}^{+\infty} \frac{1}{T}X(jk\omega_0)e^{jk\omega_0t} = \frac{1}{2\pi}\sum_{k=-\infty}^{+\infty} X(jk\omega_0)e^{jk\omega_0t}\omega_0 x~(t)=k=−∞∑+∞T1X(jkω0)ejkω0t=2π1k=−∞∑+∞X(jkω0)ejkω0tω0(8)
随着 T → ∞ T\to \infty T→∞, x ~ ( t ) \tilde x(t) x~(t) 趋近于 x ( t ) x(t) x(t),式(8)的极限就变成 x ( t ) x(t) x(t) 的表达式。再者,当 T → ∞ T\to \infty T→∞ 时,有 ω 0 → 0 \omega_0\to 0 ω0→0,式(8)的右边就过渡为一个积分。
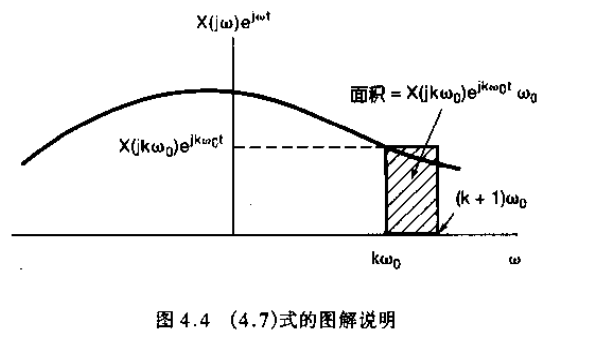
右边的每一项都可以看作是高度为 X ( j k ω 0 ) e j k ω 0 t X(jk\omega_0)e^{jk\omega_0t} X(jkω0)ejkω0t 宽度为 ω 0 \omega_0 ω0 的矩形的面积。式(8)和式(6)就分别变成
(9) x ( t ) = 1 2 π ∫ − ∞ + ∞ X ( j ω ) e j ω t d ω \tag{9}\boxed{ x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty} X(j\omega)e^{j\omega t}d\omega} x(t)=2π1∫−∞+∞X(jω)ejωtdω(9)
(10) X ( j ω ) = ∫ − ∞ + ∞ x ( t ) e − j ω t d t \tag{10}\boxed{X(j\omega)=\int_{-\infty}^{+\infty}x(t)e^{-j\omega t}dt} X(jω)=∫−∞+∞x(t)e−jωtdt(10)
(9)式和 (10)式被称为傅里叶变换对。函数 X ( j ω ) X(j\omega) X(jω) 称为 X ( t ) X(t) X(t) 的傅里叶变换或傅里叶积分,也通常被称为频谱,而 (9)式称为傅里叶反变换式。
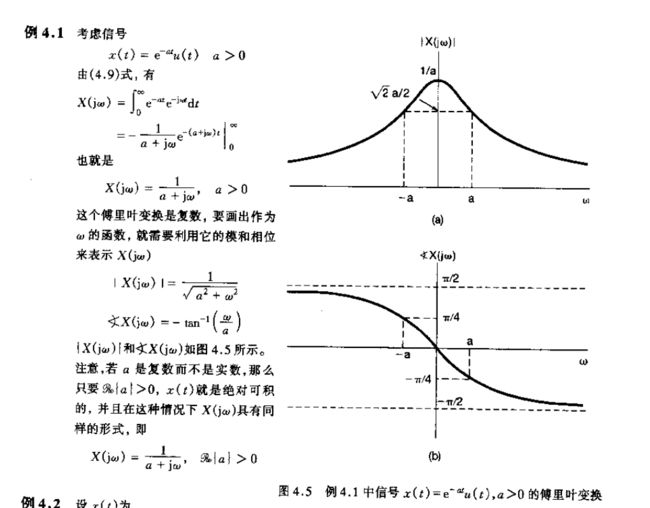
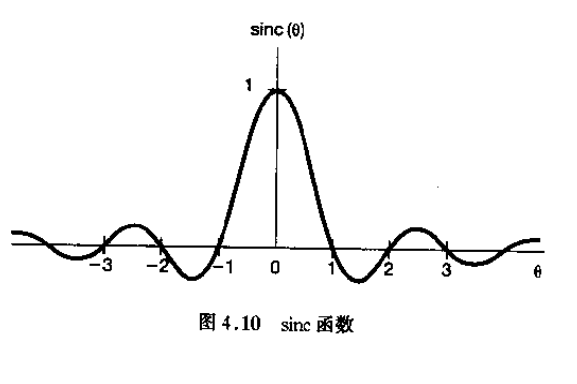
sinc 函数通常所用的形式为
(11) s i n c ( θ ) = s i n π θ π θ \tag{11} sinc(\theta)=\frac{sin\pi\theta}{\pi\theta} sinc(θ)=πθsinπθ(11)
2. 周期信号的傅里叶变换
考虑一个信号 x ( t ) x(t) x(t),其傅里叶变换 X ( j ω ) X(j\omega) X(jω) 是一个面积为 2 π 2\pi 2π,出现在 ω = ω 0 \omega = \omega_0 ω=ω0处的单独的一个冲激,即
(12) X ( j ω ) = 2 π δ ( ω − ω 0 ) \tag{12} X(j\omega) = 2\pi\delta(\omega-\omega_0) X(jω)=2πδ(ω−ω0)(12)
为了求出与 X ( j ω ) X(j\omega) X(jω) 对应的 x ( t ) x(t) x(t),可以应用式(9)的反变换公式得到
(13) x ( t ) = 1 2 π ∫ − ∞ + ∞ 2 π δ ( ω − ω 0 ) e j ω t d ω = e j ω 0 t \tag{13}x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty} 2\pi\delta(\omega-\omega_0)e^{j\omega t}d\omega=e^{j\omega_0 t} x(t)=2π1∫−∞+∞2πδ(ω−ω0)ejωtdω=ejω0t(13)
将上面的结果再加以推广,如果 X ( j ω ) X(j\omega) X(jω) 是在频率上等间隔的一组冲激函数的线性组合,即
(14) X ( j ω ) = ∑ k = − ∞ + ∞ 2 π a k δ ( ω − k ω 0 ) \tag{14} X(j\omega) = \sum_{k=-\infty}^{+\infty}2\pi a_k\delta(\omega-k\omega_0) X(jω)=k=−∞∑+∞2πakδ(ω−kω0)(14)
那么利用式(9),可得
(15) x ( t ) = ∑ k = − ∞ + ∞ a k e j k ω 0 t \tag{15} x(t) = \sum_{k=-\infty}^{+\infty}a_ke^{jk\omega_0 t} x(t)=k=−∞∑+∞akejkω0t(15)
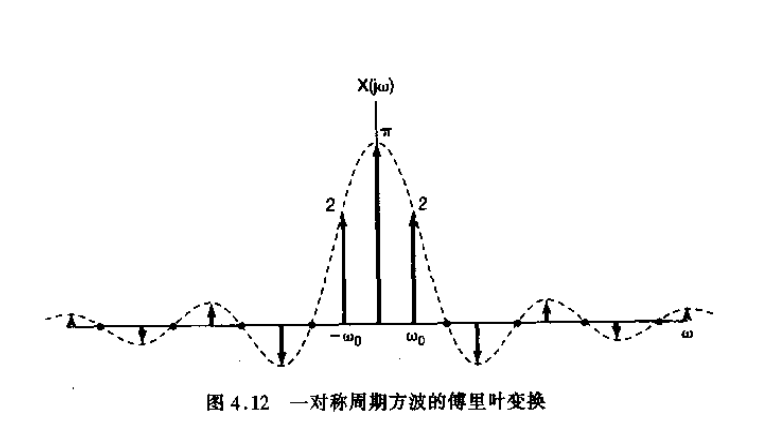
可以看出,式(15)就是一个周期信号所给出的傅里叶级数表示。因此,一个傅里叶级数系数为 { a k } \{a_k\} {ak} 的周期信号的傅里叶变换,可以看成是出现在成谐波关系的频率上的一串冲激函数,发生于第 k k k 次谐波频率 k ω 0 k\omega_0 kω0 上的冲激函数的面积是第 k k k 个傅里叶级数系数 a k a_k ak 的 2 π {2\pi} 2π 倍。

3. 连续时间傅里叶变换性质
为了方便,我们将 x ( t ) x(t) x(t) 和 X ( j ω ) X(j\omega) X(jω) 这一对傅里叶变换用下列符号表示
x ( t ) ↔ F X ( j ω ) x(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X(j\omega) x(t)↔FX(jω)
3.1. 线性
若
x ( t ) ↔ F X ( j ω ) x(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X(j\omega) x(t)↔FX(jω)
和
y ( t ) ↔ F Y ( j ω ) y(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} Y(j\omega) y(t)↔FY(jω)
则
(16) a x ( t ) + b y ( t ) ↔ F a X ( j ω ) + b Y ( j ω ) \tag{16} \boxed{ ax(t)+by(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} aX(j\omega)+bY(j\omega)} ax(t)+by(t)↔FaX(jω)+bY(jω)(16)
3.2. 时移性质
若
x ( t ) ↔ F X ( j ω ) x(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X(j\omega) x(t)↔FX(jω)
则
(17) x ( t − t 0 ) ↔ F e − j ω t 0 X ( j ω ) \tag{17} \boxed{ x(t-t_0) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} e^{-j\omega t_0}X(j\omega)} x(t−t0)↔Fe−jωt0X(jω)(17)
这个性质说明:信号在时间上移位,并不改变它的傅里叶变换的模。
3.3. 共轭及共轭对称性
若
x ( t ) ↔ F X ( j ω ) x(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X(j\omega) x(t)↔FX(jω)
则
(18) x ∗ ( t ) ↔ F X ∗ ( − j ω ) \tag{18} \boxed{ x^*(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X^*(-j\omega)} x∗(t)↔FX∗(−jω)(18)
共轭性质就能证明,若 x ( t ) x(t) x(t) 为实函数,那么 X ( j ω ) X(j\omega) X(jω) 就具有共轭对称性,即
(19) X ( − j ω ) = X ∗ ( j ω ) [ x ( t ) 为 实 ] \tag{19} \boxed{ X(-j\omega) = X^*(j\omega) \qquad [x(t) 为实]} X(−jω)=X∗(jω)[x(t)为实](19)
这就是说,傅里叶变换的实部是频率的偶函数,而虚部则是频率的奇函数。
3.4. 微分和积分
(20) d x ( t ) d t ↔ F j ω X ( j ω ) \tag{20} \boxed{ \frac{dx(t)}{dt} \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} j\omega X(j\omega)} dtdx(t)↔FjωX(jω)(20)
(21) ∫ − ∞ t x ( τ ) d τ ↔ F 1 j ω X ( j ω ) + π X ( 0 ) δ ( ω ) \tag{21} \boxed{ \int_{-\infty}^{t}x(\tau)d\tau \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} \frac{1} {j\omega} X(j\omega)+\pi X(0)\delta(\omega)} ∫−∞tx(τ)dτ↔Fjω1X(jω)+πX(0)δ(ω)(21)
3.5. 时间与频率的尺度变换
若
x ( t ) ↔ F X ( j ω ) x(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X(j\omega) x(t)↔FX(jω)
(22) x ( a t ) ↔ F 1 ∣ a ∣ X ( j ω a ) \tag{22} \boxed{ x(at) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} \frac{1}{|a|}X(\frac{j\omega}{a})} x(at)↔F∣a∣1X(ajω)(22)
若令 a = − 1 a=-1 a=−1,则有
(23) x ( − t ) ↔ F X ( − j ω ) \tag{23} \boxed{ x(-t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X(-j\omega)} x(−t)↔FX(−jω)(23)
3.6. 对偶性
3.7. 帕斯瓦尔定理
若
x ( t ) ↔ F X ( j ω ) x(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} X(j\omega) x(t)↔FX(jω)
则
(24) ∫ − ∞ + ∞ ∣ x ( t ) ∣ 2 d t = 1 2 π ∫ − ∞ + ∞ ∣ X ( j ω ) ∣ 2 d ω \tag{24} \boxed{\int_{-\infty}^{+\infty}|x(t)|^2dt =\frac{1}{2\pi}\int_{-\infty}^{+\infty}|X(j\omega)|^2d\omega } ∫−∞+∞∣x(t)∣2dt=2π1∫−∞+∞∣X(jω)∣2dω(24)
3.8. 卷积性质
(25) y ( t ) = h ( t ) ∗ x ( t ) ↔ F Y ( j ω ) = H ( j ω ) X ( j ω ) \tag{25} \boxed{y(t)=h(t)*x(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} Y(j\omega)=H(j\omega)X(j\omega)} y(t)=h(t)∗x(t)↔FY(jω)=H(jω)X(jω)(25)
两个信号在时域内的卷积就等于它们傅里叶变换的乘积。
3.9. 相乘性质
(27) r ( t ) = s ( t ) p ( t ) ↔ F R ( j ω ) = 1 2 π [ S ( j ω ) ∗ P ( j ω ) ] \tag{27} \boxed{r(t)=s(t)p(t) \overset{{\displaystyle {\mathcal {F}}}}{\leftrightarrow} R(j\omega)=\frac{1}{2\pi}[S(j\omega)*P(j\omega)]} r(t)=s(t)p(t)↔FR(jω)=2π1[S(jω)∗P(jω)](27)
两个信号在时域内的相乘就对应于频域内的卷积。
4. 傅里叶变换性质和基本傅里叶变化列表
获取更多精彩,请关注「seniusen」!
![]()