KNN的简单Python实现以及kd树的建立与搜索
KNN的简单Python实现以及kd树的建立与搜索
- KNN简介
- KNN算法实现
- kd树构建
- kd树查找
- 引用
KNN简介
通过引入如下的一个问题来进行KNN算法的阐释,如图有三种不同颜色的豆子,我们如何判定未知的三种颜色属于哪一类呢?

我们可以这样想这个问题,未知的种类的豆子离哪一类豆子的距离最近,就确定它为此种豆子。
在介绍k近邻算法之前,我们首先介绍最近邻算法,最近邻算法的定义如下:为了判断一个未知样本的类别,以全部已知类别的样本为代表点,计算未知类别 的样本到全部已知类别样本的距离,最后以与未知类别样本距离最小的样本的类别来标定这样的一个未知样本的类别。由此我们可以分析最近邻算法其实是有很大的缺陷,例如下图我们如何分析出绿色的点属于哪一种类别?

这张图可以清楚的看出来,运用最邻近算法非常容易受噪声点的干扰,而且它也不会识别出噪声点。因此,既然解决不了噪声点的问题,我们可以将噪声点的影响降低到最小,因而在此,引入了K近邻算法,即我们不再使用一个样本来判断未知样本的类别,而是扩大了参与决策的样本空间。K-近邻算法是最近邻算法的一个延伸。基本思路是:选择未知样本一定范围内确定个数的K个样本,该K个样本大多数属于某一类型,则未知样本判定为该类型。那么K的选择就显得十分重要,K如果选的较大,那么确实是能将噪声的影响降到最小,但类别之间的界限就显得较为模糊,就比如上述的例子,如果K取3,那么他就是三角形一类,如果K取5,那么它确实正方形一类。因此,在实际的操作中,一般先选一个较小 的K值,然后采用交叉验证的方式,逐渐调整K值的大小直至最后合适。
KNN算法实现
在此,基于python中的numpy库,实现了KNN的一个简易的实现版本,
算法基本步骤:
1)计算待分类点与已知类别的点之间的距离
2)按照距离递增次序排序
3)选取与待分类点距离最小的k个点
4)确定前k个点所在类别的出现次数
5)返回前k个点出现次数最高的类别作为待分类点的预测分类
具体的函数如下图所示:
def KNN(newinput,dataset,labels,k):
dis_square_mat = (dataset-newinput)**2 #求训练集中每个元素和test的差值
dis_squaresum_mat = dis_square_mat.sum(axis=1) #求距离的和值,以每一个元素为一个单位
distance = dis_squaresum_mat**0.5 #开方所求的距离之和
sorted_index = distance.argsort() #得到排序后的list的index数组
k_index = sorted_index[:k]
label_count = {}
#投票表决
for i in k_index:
if labels[i] in label_count:
label_count[labels[i]] += 1
else:
label_count[labels[i]] = 1
sorted_label_count = sorted(label_count.items(),key = lambda x:x[1],reverse=True)
return sorted_label_count[0][0]
首先通过numpy.array的形式输入数据,计算了已知类别的数据以及未知数据之间的欧几里得距离,然后由小到大进行距离的排序,并得到下标的一个list数组,取前K个数据,进行投票表决,得到最终的投票类别。
实现了KNN算法之后我们来分析这样的一个算法的优劣。KNN算法的优点是它需要调节的参数十分少,而且它不需要进行学习。
但它也存在很大的缺点,首先它很难处理那些类别极其不平衡的数据集,即:一个类的样本容量很大,而其他类样本数量很小时,很有可能导致当输入一个未知样本时,该样本的K个邻居中大数量类的样本占多数。 但是这类样本并不接近目标样本,而数量小的这类样本很靠近目标样本。这样我们可以采用权值的方法来改进。和该样本距离小的邻居权值大,和该样本距离大的邻居权值则相对较小。其次,KNN算法需要存储全部的训练样本,所占内存较大,对于十分大的数据集无法适用,第二个是计算量较大,每预测一个样本的类别都要遍历整个数据集进行运算。对于加载整个数据集的问题,无法进行改善,但对于遍历整个数据集,有方法进行改善。KNN算法的改进方法之一是分组快速搜索近邻法。其基本思想是:将样本集按近邻关系分解成组,给出每组质心的位置,以质心作为代表点,和未知样本计算距离,选出距离最近的一个或若干个组,再在组的范围内应用一般的KNN算法。由于并不是将未知样本与所有样本计算距离,故该改进算法可以减少计算量,但并不能减少存储量。
kd树构建
在进行KNN算法实现的时候,重要的是如何进行快速的k近邻搜索,尤其是在特征维度十分高的时候。k近邻法最简单的实现是线性扫描(穷举搜索),即要计算输入实例与每一个训练实例的距离(上述的实现中采用的方式)。计算并存储好以后,再查找K近邻。当训练集很大时,计算非常耗时。为了提高kNN搜索的效率,可以考虑使用特殊的结构存储训练数据,以减小计算距离的次数。
kd树(K-dimension tree)是对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是一种对k维空间的一种划分,构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分,从而构成一系列的K维超矩形区域。每一个节点对应于一个矩形区域。这样就可以很方便的进行二叉树的搜索,减少了搜索的计算量。
如图是二维kd树的一个分割实例,
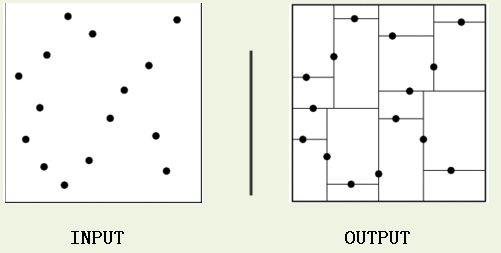
构造kd树的方法如下:首先构造一个根结点,此根结点对应的超矩形区域包含K维空间中的所有实例点;其次通过以下递归的方法,不断地对k维空间进行切分,生成子结点。【在超矩形区域上选择一个坐标轴以及在此坐标轴上的一个切分点(一般取中值),确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴,将当前超矩形区域切分为左右两个子区域(子结点);因而,实例被分到两个子区域,这个过程直到子区域内没有实例时终止(终止时的结点为叶结点)。】在此过程中,将实例保存在相应的结点上。选择中位数作为切分点的原因是,这样得到的kd树是平衡的(平衡二叉树:它是一棵空树,或其左子树和右子树的深度之差的绝对值不超过1,且它的左子树和右子树都是平衡二叉树)。
kd树构建算法步骤:
输入:k维空间数据集T={x1,x2,…,xN},其中xi=(x(1)i,x(2)i,…,x(k)i),i=1,2,…,N;
输出:kd树
(1)开始:构造根结点,根结点对应于包含T的k维空间的超矩形区域。选择x(1)即维度0为坐标轴,以T中所有实例的x(1)坐标的中位数为切分点,将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴x(1)垂直的超平面实现。由根结点生成深度为1的左、右子结点:左子结点对应坐标x(1)小于切分点的子区域,右子结点对应于坐标x(1)大于切分点的子区域。将落在切分超平面上的实例点保存在根结点。
(2)重复。对深度为j的结点,选择x(l)为切分的坐标轴,l=j%k+1,以该结点的区域中所有实例的x(l)坐标的中位数为切分点,将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴x(l)垂直的超平面实现。由该结点生成深度为j+1的左、右子结点:左子结点对应坐标x(l)小于切分点的子区域,右子结点对应坐标x(l)大于切分点的子区域。将落在切分超平面上的实例点保存在该结点。
kd树的具体构建函数如下:
class kdnode(object):
def __init__(self,dom_elt,split,left,right):
self.dom_elt = dom_elt
self.split = split
self.left = left
self.right = right
class kdtree(object):
def __init__(self,data):
self.k = len(data[0])
self.root = self.createnode(data, 0)
def createnode(self,data,split):
if not data:
return None
split_pos = len(data) // 2
data_sort = sorted(data,key=lambda x:x[split])
median = data_sort[split_pos]
split_next = (split+1) % self.k # 按顺序来进行维度选取,可以采取按方差来选取
return kdnode(median,split,self.createnode(data_sort[:split_pos],split_next),
self.createnode(data_sort[split_pos+1:],split_next))
这里采用的是坐标轮换方式来选取分割轴,当然如果是为了更高效的分割空间,可以计算所有数据点在每个维度上的数值的方差,然后选择方差最大的维度作为当前节点的划分维度。方差越大,说明这个维度上的数据越不集中(稀疏、分散),也就说明了它们就越不可能属于同一个空间,因此需要在这个维度上进行划分。这是一般集成的kd树的算法采用的分割方式。
kd树查找
构建完kd树之后,需要对整个树进行搜索,kd树的搜索比较麻烦,具体的搜索方法如下所示,
(1) 在kd树中找出包含目标点x的叶结点:从根结点出发,递归的向下访问kd树。若目标点当前维的坐标值小于切分点的坐标值,则移动到左子结点,否则移动到右子结点。直到子结点为叶结点为止;
(2) 以此叶结点为“当前最近点”;
(3) 递归的向上回退,在每个结点进行以下操作:
(a) 如果该结点保存的实例点比当前最近点距目标点更近,则以该实例点为“当前最近点”;
(b) 当前最近点一定存在于该结点一个子结点对应的区域。检查该子结点的父结点的另一个子结点对应的区域是否有更近的点。具体的,检查另一个子结点对应的区域是否与以目标点为球心、以目标点与“当前最近点”间的距离为半径的超球体相交。如果相交,可能在另一个子结点对应的区域内存在距离目标更近的点,移动到另一个子结点。接着,递归的进行最近邻搜索。如果不相交,向上回退。
(4) 当回退到根结点时,搜索结束。最后的“当前最近点”即为x的最近邻点。
kd树的具体查找函数如下:
def find_nearest(self,tree,point):
self.nearest_point = None
self.nearest_value = 0
def travel(node,depth):
if node != None:
n = len(point)
axis = depth % n
if point[axis] < node.dom_elt[axis]:
travel(node.left,depth+1)
else:
travel(node.right,depth+1)
distance = self.dis(point,node.dom_elt)
if (self.nearest_point == None):
self.nearest_point = node.dom_elt
self.nearest_value = distance
elif self.nearest_value > distance:
self.nearest_point = node.dom_elt
self.nearest_value = distance
print(node.dom_elt,depth,self.nearest_value)
if abs(point[axis] - node.dom_elt[axis]) <= self.nearest_value:
if point[axis] < node.dom_elt[axis]:
travel(node.right,depth+1)
else:
travel(node.left,depth+1)
travel(tree,0)
return self.nearest_point
def dis(self,a,b):
return ((np.array(a)-np.array(b))**2).sum()**0.5
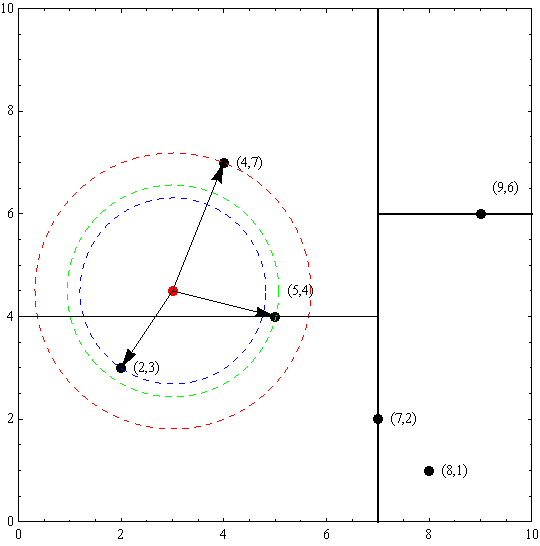
下面举个例子说明,如图所示我们已经构建好了一个kd树,我们需要搜索目标点(3,4.5)的最近邻点的最近点,首先从(7,2),搜索到(5,4),在进行查找时是由y = 4为分割超平面的,由于查找点为y值为4.5,因此进入右子空间查找到(4,7),因此首先将(4,7)作为最近点。然后回溯到(5,4),计算其与查找点之间的距离为2.06,小于当前与最近点的距离,因此将(5,4)设置为最近点。以目标查找点为圆心,目标查找点到(4,7)的距离为半径确定一个红色的圆。由于此圆的半径大于目标点到分割平面y=4的距离,因此回溯到(5,4)的另一个子空间进行查找。(2,3)结点与目标点距离为1.8,比当前最近点要更近,所以最近邻点更新为(2,3),最近距离更新为1.8,同样可以确定一个蓝色的圆。接着根据规则回退到根结点(7,2),由于蓝色圆与x=7的超平面不相交,因此不用进入(7,2)的右子空间进行查找。至此,搜索路径回溯完,返回最近邻点(2,3),最近距离1.8。

一下是kd树的整体构建及搜索代码如下:
class kdnode(object):
def __init__(self,dom_elt,split,left,right):
self.dom_elt = dom_elt
self.split = split
self.left = left
self.right = right
class kdtree(object):
def __init__(self,data):
self.k = len(data[0])
self.root = self.createnode(data, 0)
def createnode(self,data,split):
if not data:
return None
split_pos = len(data) // 2
data_sort = sorted(data,key=lambda x:x[split])
median = data_sort[split_pos]
split_next = (split+1) % self.k # 按顺序来进行维度选取,可以采取按方差来选取
return kdnode(median,split,self.createnode(data_sort[:split_pos],split_next),
self.createnode(data_sort[split_pos+1:],split_next))
def find_nearest(self,tree,point):
self.nearest_point = None
self.nearest_value = 0
def travel(node,depth):
if node != None:
n = len(point)
axis = depth % n
if point[axis] < node.dom_elt[axis]:
travel(node.left,depth+1)
else:
travel(node.right,depth+1)
distance = self.dis(point,node.dom_elt)
if (self.nearest_point == None):
self.nearest_point = node.dom_elt
self.nearest_value = distance
elif self.nearest_value > distance:
self.nearest_point = node.dom_elt
self.nearest_value = distance
print(node.dom_elt,depth,self.nearest_value)
if abs(point[axis] - node.dom_elt[axis]) <= self.nearest_value:
if point[axis] < node.dom_elt[axis]:
travel(node.right,depth+1)
else:
travel(node.left,depth+1)
travel(tree,0)
return self.nearest_point
def dis(self,a,b):
return ((np.array(a)-np.array(b))**2).sum()**0.5
引用
1.https://www.cnblogs.com/21207-iHome/p/6084670.html
2.https://blog.csdn.net/tudaodiaozhale/article/details/77327003
3.《统计学习方法》 李航 第3章 k近邻法