维特比算法解决隐马尔可夫模型解码问题（中文句法标注）
作者：白宁超
2016年7月12日14:08:28
摘要：最早接触马尔可夫模型的定义源于吴军先生《数学之美》一书，起初觉得深奥难懂且无什么用场。直到学习自然语言处理时，才真正使用到隐马尔可夫模型，并体会到此模型的妙用之处。马尔可夫模型在处理序列分类时具体强大的功能，诸如解决：词类标注、语音识别、句子切分、字素音位转换、局部句法剖析、语块分析、命名实体识别、信息抽取等。另外广泛应用于自然科学、工程技术、生物科技、公用事业、信道编码等多个领域。本文写作思路如下：第一篇对马尔可夫个人简介和马尔科夫链的介绍；第二篇介绍马尔可夫链（显马尔可夫模型）和隐马尔可夫模型以及隐马尔可夫模型的三大问题（似然度、编码、参数学习）；第三至五篇逐一介绍三大问题相关算法：（向前算法、维特比算法、向前向后算法）；最后非常得益于冯志伟先生自然语言处理教程一书，冯老研究自然语言几十余载，在此领域别有建树。（本文原创，转载注明出处：维特比算法解决隐马尔可夫模型解码问题（中文句法标注） )
目录
【自然语言处理：马尔可夫模型（一）】：初识马尔可夫和马尔可夫链
【自然语言处理：马尔可夫模型（二）】：马尔可夫模型与隐马尔可夫模型
【自然语言处理：马尔可夫模型（三）】：向前算法解决隐马尔可夫模型似然度问题
【自然语言处理：马尔可夫模型（四）】：维特比算法解决隐马尔可夫模型解码问题（中文句法标注）
【自然语言处理：马尔可夫模型（五）】：向前向后算法解决隐马尔可夫模型机器学习问题
马尔可夫个人简介
安德烈·马尔可夫，俄罗斯人，物理-数学博士，圣彼得堡科学院院士，彼得堡数学学派的代表人物，以数论和概率论方面的工作著称，他的主要著作有《概率演算》等。1878年，荣获金质奖章，1905年被授予功勋教授称号。马尔可夫是彼得堡数学学派的代表人物。以数论和概率论方面的工作著称。他的主要著作有《概率演算》等。在数论方面，他研究了连分数和二次不定式理论 ，解决了许多难题 。在概率论中，他发展了矩阵法，扩大了大数律和中心极限定理的应用范围。马尔可夫最重要的工作是在1906～1912年间，提出并研究了一种能用数学分析方法研究自然过程的一般图式——马尔可夫链。同时开创了对一种无后效性的随机过程——马尔可夫过程的研究。马尔可夫经多次观察试验发现，一个系统的状态转换过程中第n次转换获得的状态常取决于前一次（第（n-1）次）试验的结果。马尔可夫进行深入研究后指出：对于一个系统，由一个状态转至另一个状态的转换过程中，存在着转移概率，并且这种转移概率可以依据其紧接的前一种状态推算出来，与该系统的原始状态和此次转移前的马尔可夫过程无关。马尔可夫链理论与方法在现代已经被广泛应用于自然科学、工程技术和公用事业中。
1 算法原理描述
维特比算法解决：问题2（解码问题）：给定一个观察序列O和一个HMM λ=（A,B），找出最好的隐藏状态序列Q。
解码：使HMM这种包含隐藏变量的模型中，确定隐藏在某个观察序列后面变量序列的工作，叫做解码。
形式化描述：给定一个HMMλ=（A,B）和一个观察序列
作为输入，找出概率最大的状态序列
就是解码。
思想：使用前面算法找到隐藏在观察序列之后最好的状态序列，对于每个可能的隐藏状态序列，运用向前算法选出观察序列对隐藏序列的最大似然度的隐藏状态序列，从而完成解码工作，算法复杂度
，当状态序列很大时，指数级增长，计算量过大，由此采用一种动态规划算法降低算法复杂度：维特比算法。
2 维特比算法实例分析
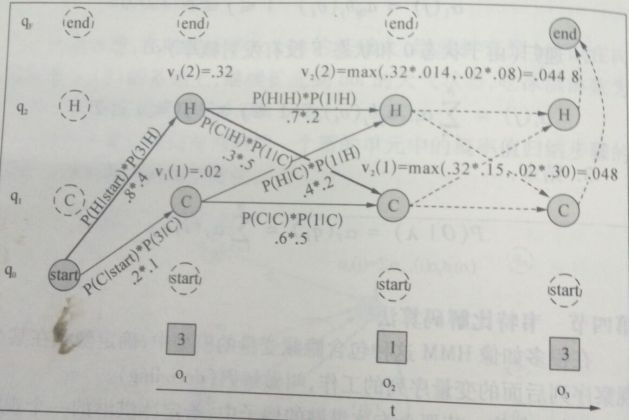
例子：通过吃冰淇淋数量（观察序列状态）计算隐藏状态空间的最佳路径（维特比网格）如下:
其中：
圆圈：隐藏状态 方框：观察状态
虚线圆圈：非法转移 虚线：计算路径
q：隐藏空间状态 o：观察时间序列状态
：在时间步t的观察状态下，隐藏状态j的概率。
Viterbi算法思想：按照观察序列由左向右顺序，每个表示自动机λ，HMM在看了头t个观察并通过了概率最大的状态序列
之后，在状态j的概率，每个 的值递归计算，并找出最大路径。
Viterbi算法形式化描述：每一个单元表示如下概率：
V的计算公式如下：
在时刻t-1的时候使用扩充前面路径的方法计算维特比概率，计算时，把下面3个因素相乘：
案例分析：
给定一个HMMλ=（A,B），HMM把最大似然度指派给观察序列，算法返回状态路径，从而找到最优的隐藏状态序列。上图是小明夏天吃冰淇淋‘3 1 3’，据此使用Viterbi算法推断最可能出现的天气状态（天气的热|冷）。
1）计算时间步1的维特比概率
计算时间步t=1和状态1的概率：
路径：start--C
计算时间步t=1和状态2的概率：
路径：start—H 较大
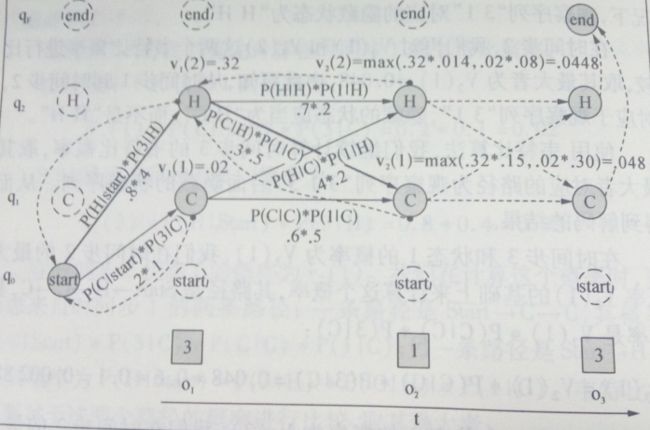
2）计算时间步2的维特比概率，在（1） 基础计算
计算时间步t=2和状态1的概率：
路径:start—H—C 较大
计算时间步t=2和状态2的概率：
路径：start—H--H
3）计算时间步3的维特比概率，在（2） 基础计算
计算时间步t=3和状态1的概率：
路径:start—H—C —C
计算时间步t=3和状态2的概率：
路径：start—H—C—H 较大
4）维特比反向追踪路径
路径为：start—H—C---H
综上所述可知：利用Viterbi算法我们知道小明夏天某天吃冰淇淋的观察值（3 1 3）推断出天气为（热 冷 热）。这也符合事实，天热吃3根，天冷吃一根。
维特比算法与向前算法的区别：
（1） 维特比算法要在前面路径的概率中选择最大值，而向前算法则计算其总和，除此之外，维特比算法和向前算法一样。
（2） 维特比算法有反向指针，寻找隐藏状态路径，而向前算法没有反向指针。
3 HMM和维特比算法解决随机词类标注问题
上面例子根据小明吃冰淇淋成功推断出天气事件，但是读者不免意犹未尽，那么下面利用同样方法进行词类标注。在随机词类标注算法中，单词是观察序列，相当于冰淇淋的数量。词类标记是隐藏状态，相当于天气的热冷。因此可以进行随机词类标注如下：
对于一个给定的句子或者单词序列，我们使用HMM词类标注算法来选择使用下面公式为最大值标记序列：
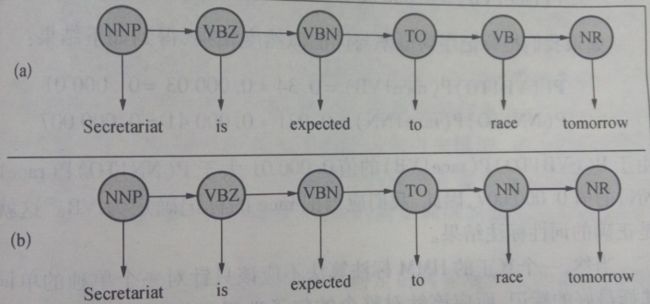
在进行词类标注时，句子“Secretariat is expected to race tomorrow”中的race是一个动词VB或者名词NN，它可以标注VB也可以标注NN，我们利用Viterbi算法解决：
根据HMM标注算法的公式可知，选择概率比较大的一个作为race的标记。P(VB|TO)*P(race|VB) 和P(NN|TO)*P(race|NN) 两者最大值即race的标记。
假设转移概率已知为：
P(NN|TO)=0.021
P(VB|TO)=0.34
假设词汇的发射概率即似然度也是知道的：
P(race|NN)=0.00041
P(race|VB)=0.00003
我们把标记序列概率和词汇发射概率相乘得到以下结果：
P(VB|TO)*P(race|VB) = 0.034*0.00003=0.00001
P(NN|TO)*P(race|NN) =0.021*0.00041=0.000007
因此，我们把race的标记确定为VB，这就是正确的词类标记结果，本质上采用统计模型的方法。当然真正使用时，我们根据需求对整个句子或者整段话以至于整篇文章进行标注，原理是一样的。
4 维特比算法描述
Viterbi算法定义：
5 利用Viterbi算法的中文句法标注
1 对文本数据清洗的预处理操作。代码略
2 对清洗后的文本，采用有监督方法对古文献BIO标记（B表示句子开始I表示句子中间O表示句子结尾）代码略
3 统计文本的转移矩阵B。 代码略
4 统计文本的发射矩阵A。 代码略
5 维特比解码算法找出观察序列O的最后的隐藏状态序列Q
5.1 隐马尔可夫模型中维特比解码算法序列标注
String observationStr="病有发热恶寒者；发于阳也，无热恶寒者；发于阴也。";//观察序列
String[] states={"B","I","O"};//状态序列
double start_probability=0.3333;//初始状态概率
String str="书名：伤寒论。作者：张仲景。朝代：东汉。";
String stateStr=MethodUilt.Vitrerbi(str, start_probability, Amatrixpath, Bmatrixpath);//隐藏状态序列，即隐含马尔科夫模型的词类标注
System.out.println("观察序列：\t"+str.replaceAll("", "\t")+"\n标注序列：\t\t"+stateStr);
5.2 针对马尔科夫模型中第二个问题，采用维特比算法进行句子标注，其中主要还是动态规划思想
/**
* 针对马尔科夫模型中第二个问题，采用维特比算法进行句子标注，其中主要还是动态规划思想
* @param observationStr 观察序列
* @param states 状态序列
* @param start_probability 初始化状态,即π
* @param Amatrixpath 发射矩阵路径
* @param Bmatrixpath 转移矩阵路径
* start_probability, transititon_probability, emission_probability
* @return
*/
public static String Vitrerbi(String observationStr,double start_probability,String Amatrixpath,String Bmatrixpath){
//将观察序列切词存储在数组里面
String[] ObserArr=observationStr.split("");
//将发射矩阵放入数组中
String[] emissionArrs=HeplerUilt.readStrFile(Amatrixpath, "\n").split("\n");//文本中发射矩阵逐次切割放于一位数组中
Map countMap=new HashMap();//实例化map，存储：词+实体（二维数组）
for(int i=0;i entry : countMap.entrySet()){
if(entry.getKey().equals(tarWord)){
double emission_probability=HeplerUilt.getMax(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());
String prior=HeplerUilt.compareMark(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());
list.add(prior);
V=start_probability*emission_probability;
//System.out.println(tarWord+":"+start_probability+":"+emission_probability+":"+prior+":"+HeplerUilt.DecFormat(4,V));
}
}
//观察序列O，第二个状态到结束
for(int i=2;i entry : countMap.entrySet()){
String q=list.get(list.size()-1).toString();//获取前一个标注
if(entry.getKey().equals(ObserArr[i])){ //获取观察序列的发射概率
double max_probability=HeplerUilt.getMax(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());//得到最大发射概率值
double transititon_probability=HeplerUilt.getMaxTrans(q,transArr); //获取最大的转移概率
String prior=HeplerUilt.compareMark(entry.getValue().getXb(), entry.getValue().getXi(), entry.getValue().getXo());//得到最大发射概率的标注
list.add(prior);//将最大发射概率进行保存
V=V*max_probability*transititon_probability;//得到下一步的V值
//测试数据
//System.out.println(ObserArr[i]+":"+max_probability+":"+transititon_probability+":"+prior+":"+HeplerUilt.DecFormat(4,V));
}
}
}
//System.out.println(observationStr.length()+":"+list.size());
for(int i=0;i 6 实验结果：
3 参考文献
【1】统计自然语言处理基础 Christopher.Manning等 著 宛春法等 译
【2】自然语言处理简明教程 冯志伟 著
【3】数学之美 吴军 著
【4】Viterbi算法分析文章 王亚强
声明：关于此文各个篇章，本人采取梳理扼要，顺畅通明的写作手法。一则参照相关资料二则根据自己理解进行梳理。避免冗杂不清，每篇文章读者可理清核心知识，再找相关文献系统阅读。另外，要学会举一反三，不要死盯着定义或者某个例子不放。诸如：此文章例子冰淇淋数量（观察值）与天气冷热（隐藏值）例子，读者不免问道此有何用？我们将冰淇淋数量换成中文文本或者语音（观察序列），将天气冷热换成英文文本或者语音文字（隐藏序列）。把这个问题解决了不就是解决了文本翻译、语音识别、自然语言理解等等。解决了自然语言的识别和理解，再应用到现在机器人或者其他设备中，不就达到实用和联系现实生活的目的了？本文原创，转载注明出处：维特比算法解决隐马尔可夫模型解码问题（中文句法标注）