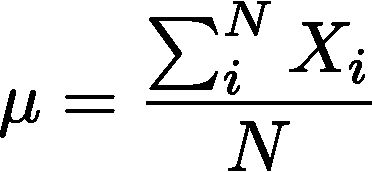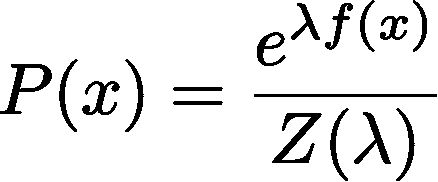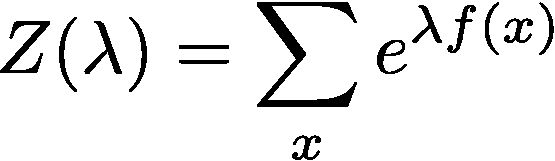“参数估计是…通过测量或经验数据来估计概率分布参数的数值”—Wikipedia如是说。
可是我们最熟悉的最小二乘估计不是没有概率分布么?不,它实际上是高斯分布的估计—我在上一章如是说。
绕过了这道坎,我们就能站在概率论的角度考虑问题了。
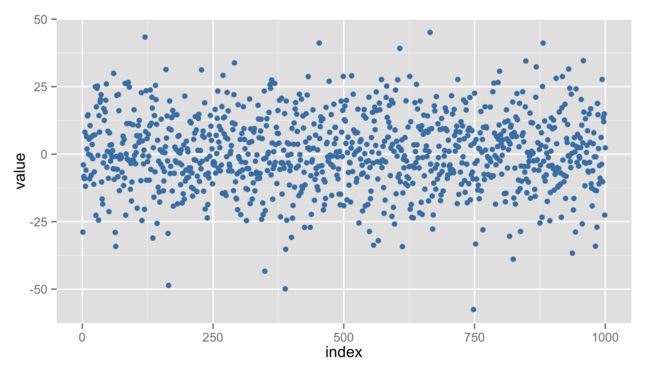
这时我们会发现各种各样的参数估计方法,例如极大似然估计、最大后验估计、贝叶斯推断、最大熵估计,等等。虽然方法各不相同,但实际上背后的道理大体一样。想要了解它们之间的联系与区别,只要举一个最简单的例子就可以了:观测到一堆从某个高斯分布产生的数值,请估该计高斯分布的参数之一—均值。下图就是我们的实验数据:从一个0均值一维高斯分布中产生的1000个点,横坐标是数据的序号(1:1000),纵坐标是样本点的值。
1. 极大似然估计(MLE)
怎样的参数是最好的?使得观测数据出现的概率(即所谓likelihood,似然)最大的参数就是最好的。这个朴素的思想,就是极大似然估计(Maximum Likelihood Estimation, MLE)。对一个独立同分布(i.d.d)的样本集来说,总体的似然就是每个样本似然的乘积。例如本例中的似然(Likelihood)显然是:
在实际中,因为连乘计算起来比较麻烦,并且概率都很小,难免越乘越接近0最终引发数值bug,因此多对其取log, 得到log似然( log likelihood):
log并不改变似然函数的凸性,因此可令其对u取极值,显然得到:
这就完成了对高斯分布均值的极大似然估计。值得一提的是,该例的log似然实在是太简单,所以这个极值可以直接求导得到;在更多的情况下,我们需要通过梯度下降法等最优化算法来求解。而绝大部分最优化的工具包都默认求函数的最小值,因此别忘了把你的log似然乘以-1变成负log似然(Negative Log Likelihood),在你把它塞给一个最优化工具包之前。
2.最大后验估计(MAP)
MLE简单又客观,但是过分的客观有时会导致过拟合(Over fitting)。在样本点很少的情况下,MLE的效果并不好。为此,贝叶斯学派发明了最大后验估计(Maximum a Posterior)。先看一个最简单的概率图模型,借此来复习一下先验、似然、后验:
likelihood:对一个待估参数θ来说,它产生观测样本x的概率密度函数p(x|θ)叫做x的似然;
prior:θ本身是一个未观测到的变量,既然未观测到,也就是可以看成一个随机变量,假设其服从以α为参数的概率分布p(θ|α),叫做θ的先验;
posterior:在观测到x之后,我们对θ的认识得到了增强,将它的概率分布修正为p(θ|α,x),这个就叫做θ的后验;简单套用一下贝叶斯公式,可以得到后验分布:
即先验和似然的乘积。在本文的例子中,假设我们预先知道均值u本身服从一个高斯分布,其均值为u0,方差为σ0,那么观测到数据样本之后,u的后验分布为:
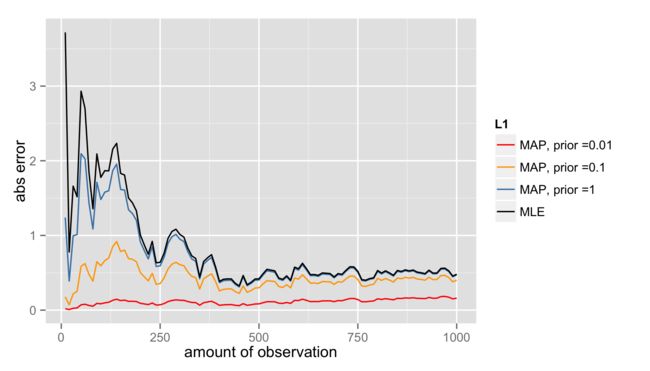
接下来就和MLE完全一样了:求一个u使得后验概率最大即可。方便起见,把u0固定成0,变化σ0做几组对比实验:
横轴是参数估计所用到的样本数,纵轴是估计值与真实值之间的误差。σ0取了0.01、0.1、1等三个值,作为方差,值越小先验的强度越大。
可见:
1) MLE在数据较少时不准确
2) 先验强的MAP(图中红线、黄线)可以在少量数据时就达到较好的结果
3) 先验弱的MAP(图中蓝线)退化为MLE
还有一点在图中看不出来:假如我们预先知道的关于u的信息是不对的,即选择了一个强但偏离实际的先验(例如把u0设置成5, σ0设置成0.01)会怎样?其实那样的话结果甚至还不如MLE,这也是贝叶斯学派广为诟病的硬伤之一:凭什么去选择先验?大部分时候,我们选一个方便计算但不包含太多信息的共轭先验(什么是共轭先验?下回分解)。
3.贝叶斯推断(Bayesian Inference)
其实MAP不仅让频率学派的人不领情,甚至不能令苛刻的贝叶斯学派满意。
一来,MAP只取后验分布的峰值(众数,mode),而mode往往不具有很强的代表性(特别是在多峰的函数中);
二来,MAP有一个独特的缺点,对参数形式敏感。如果我们要估计方差,就会发现,将方差作为参数得到的解,并不是将标准差作为参数得到的解的平方。而MLE可不会这样。
那么与其将后验分布的峰值拿来凑合,还不如将整个后验分布求出来,用一个分布来描述待估的参数。这就是Inference。
可是我们刚才在MAP中不是已经求出了整个后验分布么?是的,这是因为例子太简单了。在绝大部分超过三个节点的概率图模型中,都无法求出精确的后验分布,我们需要借助于各种各样的近似手段,于是才有了拉普拉斯近似、变分推断、Gibbs采样…等等等等,内容庞杂,下回再表。
4.最大熵估计
前例中的估计无不建立在这样一个基础上:已知分布的形式,求分布的参数。但是如果并不知道分布的形式,还能估计么?答案是不仅可以,并且靠谱。这就是鼎鼎有名的最大熵法。关于怎么样从最大的熵原理推导出最大熵估计,已经有足够多的介绍,在这里就不说了。
我们要说的是,其实最大熵估计也是一种MLE。
首先,我们不知道样本的分布形式,但是它作为一个概率分布,一定会满足
1)处处非负
2)和为1
于是,可以随意构造一个这样的函数:
其中
指数保证了非负,Z保证了归一化,因此f(x)可以构造成任意一个关于x的函数--茫茫大海中,总会有一个f(x)使得p(x)接近样本的真实分布。
现在我们来对这个分布做MLE,其log似然是:
这个log似然对λ来说是凸的,因此使用简单的优化算法(比如梯度下降),就可以求得一个最优的λ,把λ代入p(x)的通项公式中,就可以得到分布的具体形式。特别的,当我们取f(x)=(x,x2)时,所得结果就是一个高斯分布。从另一方面来说,估计的结果严重依赖于选择怎样的f(x),这一点和MAP有些类似。
-这个结果和最大熵估计完全等价。也就是说,最大熵估计等同于对以下形式的模型的MLE:
而这种形式的模型,被统一称作“对数线性模型”(log linear model)。它是logistic回归、最大熵模型、以及以条件随机场(CRF)为代表的各种概率无向图的的基础。