KD树 球树
KD树
1.KD树建树采用的是从m个样本的n维特征中,分别计算n个特征的取值的方差,用方差最大的第k维特征 nk来作为根节点。选择特征 nk的取值的中位数 nkv对应的样本作为划分点,对于所有第k维特征的取值小于 nkv的样本,划入左子树,对于第k维特征的取值大于等于 nkv的样本,划入右子树,对于左子树和右子树,采用和刚才同样的办法来找方差最大的特征来做更节点,递归的生成KD树。
2.流程图

3.二维样本6个,{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},构建kd树的具体步骤为:
1)找到划分的特征。6个数据点在x,y维度上的数据方差分别为6.97,5.37,所以在x轴上方差更大,用第1维特征建树。
2)确定划分点(7,2)。根据x维上的值将数据排序,6个数据的中值(所谓中值,即中间大小的值)为7,所以划分点的数据是(7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于:划分点维度的直线x=7;
3)确定左子空间和右子空间。 分割超平面x=7将整个空间分为两部分:x<=7的部分为左子空间,包含3个节点={(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点={(9,6),(8,1)}
4)用同样的办法划分左子树的节点{(2,3),(5,4),(4,7)}和右子树的节点{(9,6),(8,1)}。最终得到KD树
4.最后得到的KD树如下:

3. KD树搜索最近邻:
首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心,以目标点到叶子节点样本实例的距离为半径,得到一个超球体,最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点,检查另一个子节点包含的超矩形体是否和超球体相交,如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了,直接返回父节点的父节点,在另一个子树继续搜索最近邻。当回溯到根节点时,算法结束,此时保存的最近邻节点就是最终的最近邻
球树
KD树算法虽然提高了KNN搜索的效率,但是在某些时候效率并不高,比如当处理不均匀分布的数据集时,不管是近似方形,还是矩形,甚至正方形,都不是最好的使用形状,因为他们都有角。一个例子如下图:

球树,顾名思义,就是每个分割块都是超球体,而不是KD树里面的超矩形体。
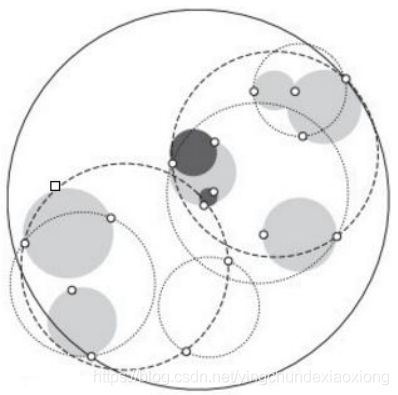
建树流程
1) 先构建一个超球体,这个超球体是可以包含所有样本的最小球体。
2) 从球中选择一个离球的中心最远的点,然后选择第二个点离第一个点最远,将球中所有的点分配到离这两个聚类中心最近的一个上,然后计算每个聚类的中心,以及聚类能够包含它所有数据点所需的最小半径。这样我们得到了两个子超球体,和KD树里面的左右子树对应。
3)对于这两个子超球体,递归执行步骤2)最终得到了一个球树。
使用球树找出给定目标点的最近邻方法是首先自上而下贯穿整棵树找出包含目标点所在的叶子,并在这个球里找出与目标点最邻近的点,这将确定出目标点距离它的最近邻点的一个上限值,然后跟KD树查找一样,检查兄弟结点,如果目标点到兄弟结点中心的距离超过兄弟结点的半径与当前的上限值之和,那么兄弟结点里不可能存在一个更近的点;否则的话,必须进一步检查位于兄弟结点以下的子树。检查完兄弟节点后,我们向父节点回溯,继续搜索最小邻近值。当回溯到根节点时,此时的最小邻近值就是最终的搜索结果。
sklearn_example
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
n_neighbors = 15
# import some data to play with
iris = datasets.load_iris()
# we only take the first two features. We could avoid this ugly
# slicing by using a two-dim dataset
X = iris.data[:, :2]
y = iris.target
h = .02 # step size in the mesh
# Create color maps
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
for weights in ['uniform', 'distance']:
# we create an instance of Neighbours Classifier and fit the data.
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(X, y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, weights = '%s')"
% (n_neighbors, weights))
plt.show()