redis（22）--二进制位数组

Redis提供了SETBIT,GETBIT,BITCOUNT,BITOP四个命令用于处理二进制位数组(bit array,又称"位数组").

位数组的表示

使用SDS结构保存位数组，使用SDS的操作函数处理位数组。但是，为了简化SETBIT的实现，保存位数组的顺序和我们平时书写位数组的顺序是相反的，如设置0000 1010，保存在SDS中是0101 0000。

位数组：1111 0000 1100 0011 1010 0101 在SDS中保存为 1010 0101 1100 0011 0000 1111

GETBIT命令的实现

GETBIT

过程如下：

-1、计算byte = [offset / 8],byte记录了offset偏移量指定的二进制位保存在位数组的哪个字节；
-2、计算bit = (offset mod 8) + 1,bit记录了offset偏移量指定的二进制位是byte字节的第几个二进制位；
-3、根据byte和bit的值，在位数组中定位偏移量指定的二进制位，并返回这个位的值。
复杂度O（1）.

 

SETBIT命令的实现

SETBIT

1、计算len=[offset / 8] + 1，len记录了保存offset偏移量指定的二进制位至少需要多少字节；
2、检查bitarray键保存的位数组长度是否小于len，如果是，扩展SDS长度为len字节，并将所有扩展的长度值置为0；
3、计算byte = [offset / 8]，byte记录了offset偏移量指定的位保存在哪个字节；
4、计算bit = (offset mod 8) + 1,bit记录了offset偏移量指定的二进制位是byte字节的第几个二进制位；
5、根据byte值和bit值，在bitarray键保存的位数组中定位offset指定的二进制位，先记录指定二进制位保存的值到oldvalue，然后将新值设置为这个二进制位的值；
6、向客户端返回oldvalue。
复杂度（O）1；

BITCOUNT命令的实现

BITCOUNT

统计给定位数组中，值为1的二进制位的数量。

二进制位统计算法：

1、遍历算法：，遍历每个二进制位，在遇到值为1的位时，计数器+1；
效率太低，每次循环正检查一个二进制位的值是否为1，检查操作执行的次数与位数组包含的二进制位数量成正比。
2、查表算法：
对于一个有限集合来说，集合元素的排列方式是有限的；
对于一个有限长度的位数组来说，它能表示的二进制位排列也是有限的。
创建一个数字对应位为1个数的表，通过一次读取一个（或多个，需要建更大的映射表）字节，对比数字，就可以知道这个字节有几个位为1。键为数字，值为位上1的个数，查表。
初看起来，只要我们创建一个足够大的表，那么统计工作就可以轻易地完成，但查表法的实际效果会受到内存和缓存两方面因素的限制：

• 因为查表法是典型的空间换时间策略，节约的时间越多，花费的内存越大。
• 查表法的效果会受到CPU缓存的限制：对于固定大小的CPU缓存，创建的表越大，CPU缓存所能保存的内容相比整个表越少，那么查表时出现缓存不命中的情况就会越多，缓存换入和换出操作就会越频繁，最终影响查表法的效率。

3、variable-precision SWAR算法
BITCOUNT命令要解决的问题：统计一个位数组中非0二进制位的数量，在数学上被称为“计算韩明重量”。汉明重量经常被用于信息论，编码理论和密码学，所以研究人员开发了多种不同的算法，一些处理器甚至直接带有计算汉明重量的指令，对于不具备这种特殊指令的处理器来说，variable-precision SWAR算法是效率最好的，该算法通过一系列位移和位运算，可以在常数时间内计算多个字节的汉明重量，并且不需要额外的内存。

以下是一个处理32位长度位数组的算法实现：

uint32_t swar(uint32_t i){
 //步骤1
 i = (i & 0x55555555) + ((i >> 1) & 0x55555555);
 //步骤2
 i = (i & 0x33333333) + ((i >> 2) & 0x33333333);
 //步骤3
 i = (i & 0x0f0f0f0f) + ((i >> 4) & 0x0f0f0f0f);
 //步骤4
 it = (i * (0x01010101) >> 24);
 return i
}

执行步骤:

1、计算出值i的二进制标志可以按每两个二进制位为一组进行分组，各组的十进制表示就是改组的汉明重量；

2、计算出的值i的二进制表示可以按每四个二进制位为一组进行分组，各组的十进制表示就是改组的汉明重量；

3、计算出的值i的二进制表示可以按每八个二进制位为一组进行分组，各组的十进制表示就是该组的汉明重量。

4、i*0x01010101计算出bitarray的汉明重量并记录在二进制位的最高八位，而>>24通过右移运算，将bitarray的汉明重量移动到最低八位，得出的结果就是汉明重量。

因为swar函数是单纯的计算操作，所以它无需像查表法那样，使用额外的内存。而且swar函数是一个常数复杂度的操作，所以我们可以按照自己的需要，在一次循环中多次执行swar，从而按倍数提升计算汉明重量的效率。

我们可以按照自己的需要，再一次循环中多次执行swar，从而按倍数提升计算汉明重量的效率：例如，我们在一次循环中调用两次swar函数，那么计算汉明重量的效率就从之前的一次循环计算32位提升到了一次循环计算64位。如果在一次循环中调用四次swar函数，那么一次循环级就可以计算128个二进制的汉明重量，这笔每次循环只调用一次swar函数块4倍。

当然，一次循环执行多个swar调用这种优化方式是有极限的：一旦循环中处理数组的大小超过了缓存大小，这种优化的效果就会降低并最终消失。

 

variable-precision SWAR逐行解释：

第一行

i = i - ((i >> 1) & 0x55555555);

0x55555555二进制的标识方式如下：

0x55555555 = 0b01010101010101010101010101010101

可以看到的规律是，奇数位为1,偶数位为0。
表达式((i >> 1) & 0x55555555)，将i右移一位，并将所有偶数位设置为0.（等效的，我们也可以通过& 0xAAAAAAAA将所有奇数位设置成0，然后再将结果右移1位）为了方便起见，我们将这个中间值命名为j。
当我们将中间值j从原始值i中减去会发生什么？那让我们来看看如果i只有两位是什么情况。

    i           j （右移一位）        i - j
----------------------------------
0 = 0b00    0 = 0b00    0 = 0b00
1 = 0b01    0 = 0b00    1 = 0b01
2 = 0b10    1 = 0b01    1 = 0b01
3 = 0b11    1 = 0b01    2 = 0b10

最后的结论就是i-j的十进制结果就是位数组中1出现的次数。
那么如果i不只是两位数组呢？实际上，很容易发现i-j的最低两位仍然如上表所示，三四位，五六位也是一个道理，等等。需要注意的是：

• 由于& 0x55555555的巧妙用法，尽管>> 1，i-j的最低两位不会被i的第三位或者更高的位影响。
• 由于j的最低两位永远不可能在比i的最低两位大。这个减法永远不会向i的第三位借位，因此：对于i-j来说，i的最低两位不会影响i的第三位或者更高位。

实际上这一行就是将32位数组分为16个两位为单位的组，每组分别计算1出现的次数。
第二行：

i = (i & 0x33333333) + ((i >> 2) & 0x33333333);

与第一行对比，这一行非常的简单。首先，来看一下0x33333333的二进制表示：

0x33333333 = 0b00110011001100110011001100110011

i & 0x33333333的目的是以4位为分组取四位中的后两位。而(i >> 2) & 0x33333333在把i右移两位后做同样的工作。然后把它们结果加起来。
因此，实际上，这行做的工作就是将最低的两位1出现的次数和最低三四位的1出现的次数相加，得到最低四位的1出现的次数。同样的对于输入的8个四位分组（=16进制数）都是一样的。
第三行：

return (((i + (i >> 4)) & 0x0F0F0F0F) * 0x01010101) >> 24;

(i + (i >> 4)) & 0x0F0F0F0F除了这次是用临近的4位1出现的次数系相加，得到8位为一组的1出现的次数，以外原理跟前一行一样。（和上一行有所不同的是，我们可以把&去掉，因为我们知道原始输入8位不可能出现超过8个1因此二进制值不会超过4位。）
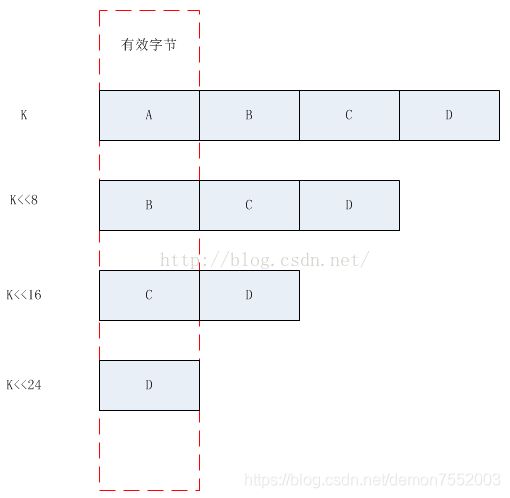
现在我们有一个三十二位数，由四个字节组成，每个字节保存着原始输入中为1的位的数量。（我们把它们称作A，B，C和D。）那么为什么我们用0x01010101乘以这个值（命名为k）？

由于：

0x01010101 = (1 << 24) + (1 << 16) + (1 << 8) + 1

可得：

k * 0x01010101 = (k << 24) + (k << 16) + (k << 8) + k

k * 0x01010101最高位就是原始输入的1出现次数的最终结果。>> 24只是简单的将最高位的值移到最低位。

Redis实现

BITCOUNT命令的实现用到了查表和variable-precisionSWAR两种算法：

• 查表算法使用键长为8位的表，表中记录了从0000 0000 到1111 1111在内的所有二进制位的汉明重量。
• variable-precisionSWAR算法，BITCOUNT命令在每次循环中载入128个二进制位，然后调用四次32位variable-precision算法来计算这128个二进制位的汉明重量。

程序会根据未处理的二进制位的数量来决定使用哪种算法：
如果未处理的二进制位数量小于128位，那么程序使用查表法来计算二进制位的汉明重量。否则使用variable-precisionSWAR算法来计算二进制位的汉明重量。

BITTOP

因为C语言直接支持对字节执行逻辑与，或，异或，非的操作，所以BITOP的四个操作都是直接基于这些逻辑操作来实现的。
执行过程：
1、创建一个空白的位数组value，用于保存逻辑操作的结果；
2、对两个位数组的每个字节执行逻辑操作，并将结果保存到value[i]字节；
3、经过前面的逻辑操作，程序得到了计算结果，并将它保存在result上。

BITTOP AND   [operand-2]

BITTOP OR   [operand-2]

BITTOP NOT   [operand-2]

BITTOP XOR   [operand-2]