我还是第一次这么尴尬的写这种东西
首先%%%wangkoala学长!
一部分是对着PowerPoint写的~
简述一下学习成果~
1>卡特兰数
$Catalan$(这里用$h_i$来表示第$i$号卡特兰数)
首先是一个递推公式:
$h_n=h_0 \times h_{n-1}+h_1 \times h_{n-2} + \cdots + h_{n-1} \times h_0(n \geq 2)$
所以满足这个形式的就可以按卡特兰数处理咯
随后是通项公式:
$\begin{array}{lcl}h_n & = & C_{2n}^n-C_{2n}^{n-1}\\ & = & \frac{C_{2n}^n}{n+1}\end{array}$
应用:
1.求一个二叉树的形态方案数
2.求出入栈的顺序方案数
3.求有限制的方格行走方案
4.括号匹配
而且这些都可以转化成一个问题:把$1$和$-1$排列在数组中使前缀和大于$0$
1.可以把左儿子记为$1$右儿子记为$-1$,然后优先向左搜索。
2.可以把入栈记为$1$出栈记为$-1$
来个证明
首先设$k$为最后出栈的元素,
那么前面的元素必须在$k$压入之前弹出(不然$k$就不是最底层了)
后面的元素弹栈也必须弹出,才能把$k$弹出
这样就有式子:
$f_i=\sum\limits_{k=1}^{i}f_{k-1} \times f_{i-k}$
唔,我感觉和某个式子好像~~
对,就是递推公式!!!
3.这样的就是裸的:「链接」
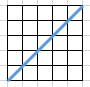
只能向右向上,不能穿越蓝线
那,怎么算方案?
其实还是$Catalan$数。
一种是你把向右记为$+1$,向上记为$-1$这样就可以按公式求了
总共是$2n$个加和减,所以是$h_n$
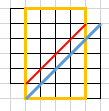
加上翻折
首先就是划一条辅助线,这条线是非法路径必须要过的
然后翻折非法路径接触红线后的部分
(顺带把网格也翻过去)
于是答案就是
$C_{2n}^n-C_{2n}^{n-1}$
即:到终点的方案减到非法终点的方案
到终点走了$2n$步,其中向右占$n$步,就是$C_{2n}^n$
到非法重点走了$2n$步,其中向右占$n-1$步,是$C_{2n}^{n-1}$
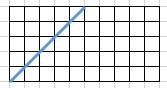
然后还有一个提升版!
问题一样
翻折:
到终点:走$n+m$步,向右占$n$就是$C_{n+m}^n$
到非法终点:走$n+m$步,向右占$m-1$就是$C_{n+m}^{m-1}$
答案就是:
$C_{n+m}^n-C_{n+m}^{m-1}(n \geq m)$
这里用向上也一样,只是答案化为:
$C_{n+m}^m-C_{n+m}^{n+1}(n \geq m)$
这不是公式$C_n^m=C_n^{n-m}$么(笑)
一番公式化简:($LaTex$练习)
$\begin{array}{lcl}C_{n+m}^n-C_{n+m}^{m-1} & = & \frac{(n+m)!}{n! \times m!}-\frac{(n+m)!}{(m-1)! \times (n+1)!}\\ & = & \frac{(n+m)! \times (n+1-m)}{(n+1)! \times m!}\\ & = & \frac{(n+m) \times \cdots \times (n+2) \times (n+1-m)}{m!}\end{array}$
用高精乘低精和高精除低精就可以了。
2>prufer序列
首先说一句:每一颗不同的无根树有且仅有唯一prufer序列与之对应。
且prufer序列与无根树可以互相转换。
转换顺序是规定好的。
树转序列
在无根树上,进行如下操作(提前建立一个数列$M$,叫数组也一样)
1.找到编号最小的度数为$1$的点
2.然后把这个点删掉(把它连的边也一起删掉),与它有边相连的点加入$M$
3.不断重复1.2.操作,直至树中只剩下两个点
我们的数列$M$就是prufer序列。
序列转树
(如果不能转树这个序列就几乎没用了)
首先定义集合$G=\{1,2,3,\cdots,n\}$
取prufer序列$M$进行如下操作:
1.取$M$中最靠前元素,与$G$中存在但不存在于$M$的点连边
2.删除$M$,$G$中连边的两个元素
3.重复以上操作,直至$G$中只剩两个点(然后这两个点连边就完了)
因为一一对应,所以无根树和prufer序列是数量一致的
那么就有:$n$个节点的无根树的个数为$n^{n-2}$
于是有根树的个数:$n^{n-1}$(随便选一个点做根)
枚举起来很方便的!
然后因为每次有边才能加入$M$,有式子:度数=$M$中出现次数+1
这样度数确定的点也可以枚举
有:
$\frac{(n-2)!}{(d_1-1)! \times (d_2-1)! \times \cdots \times (d_n-1)!}$
也许这个公式不好理解(但是好用啊啊):推导
首先要说的是原始公式:
$C_{n-2}^{d_1-1} \times C_{n-d_1+1-2}^{d_2-1} \times \cdots \times C_{n-d_1-\cdots-d_n+n-2}^{d_n-1}$
就是说把$d_x-1$个点放入$n$个空里。
然后把剩下的放进剩下的空里(全排列)
花间(化简):
$\begin{array}{lcl} & = & \frac{(n-2)!}{(d_1-1)! \times (n-d_1+1-2)!} \times \frac{(n-d_1+1-2)!}{(d_2-1)! \times (n-d_1-d_2+2-2)!} \times \cdots \\ & = & \frac{(n-2)!}{(d_1-1)! \times (d_2-1)! \times \cdots \times (d_n-1)!}\end{array}$
3>线性基
这个就是求异或和的一个工具。
就是说,用原来一堆数异或出来的结果值域和用线性基一样。
其实这个不是这个时候讲的,但是我怕我忘了^_^
类比于向量的基底,这个是异或和的基底。
向量中有多维,每一维不互相影响。
二进制数有多位,在异或意义下不互相影响
用基底可以表示所有向量(平面/空间向量基本定理)(某G姓老师讲的很清楚)
可以这么说:虽然相互垂直的向量表示其它向量容易,但只要不共面就能表示空间向量,只要不共线就可以表示平面向量
类比的说,线性基是每一个二进制位上的基底,基底不一定是完全互相不影响的,而我们的目的是表示值域内所有数,并非更方便的表示一切数
这就解释了我们为什么用插入的方式更新基底而非直接用$0 \cdots 010 \cdots 0_{(2)}$这样的数做基底
下面是伪代码(解释一番)
for i=60 to 0 首先要枚举二进制上的每一位,由高到低
if(x的第i+1位为1) 随后,找到二进制的最高位。我们找最高位
{ 是因为我们优先要考虑可以表示的最大的数而非更细致的数
if(d[i]为0) 如果没有可以表示的基底加进去。
{
d[i]=x;
break;
}
else x=x^d[i]; 如果有基底,我们就用基底去表示它,这样如果表示了
} 就不用加新的基底。
最后的 else 着重说一句。
异或是可逆的(暂且这么说)
$x\ xor\ y\ xor\ y = x$
所以我们用这个基底去拆插入的数。
这样就可以表示值域内的数。
这样我们怎么找最小的异或和?
直接把最小的有数基底输出。
如何找最大以及第$k$大呢?
这个只输出最大基底显然是错的,基底全异或也不对(不能保证异或和值单调)
那么我们就需要对基底进行处理。
我觉得就是用基底表示了基底。
把有数的基底$d_i$去处理别的基底$d_j(j > i)$
使其第$i$位为$0$,如果本来就是$0$就不用管它。
例:($X$表示未知,即$0$或$1$)
$\begin{array}{cc} \begin{array}{cc}0 & 1 & 0 & 1 & X & X & \cdots \\ 0 & 0 & 1 & 1& X & X & \cdots\\0 & 0 & 0 & 1 & X & X & \cdots\end{array}\\ \vdots \\ \Downarrow \\ \begin{array}{cc}0 & 1 & 0 & 0 & X & X & \cdots \\ 0 & 0 & 1 & 0 & X & X & \cdots \\ 0 & 0 & 0 & 1 & X & X & \cdots \end{array} \\ \vdots\end{array}$
这样就满足单调性了,最大值就可以求了。
但是第$k$大怎么求啊??
可以利用状压思想。
把最后一位记为最低位。
$1$是异或$0$是不异或。
这样数越小就异或和就越小咯!
意思就是:
先把有数的基底堆在下面,处理完。
然后把最下面叫做最低位,最上面叫最高位。
这样,$00001$是最小的,$00010$第二小,$00011$第三小,以此类推。
4>BSGS($\mathcal{Baby\ Step\ Giant\ Step}$)
适用于形如:
$A^x \equiv B (mod\ p)$
的式子求解$x$。
这里可以分情况求解。
1>p是质数
由费马小定理可知:$a^{p-1} \equiv 1 (\mbox{mod}\ p)$
这样$x$就一定小于$p-1$
设整数$m=\sqrt{p}$
这时,$x$就可以表示成:$i*m+j$
然后枚举$j$,可以用$\mathsf{hash}$表存一下
枚举$i$,在$\mathsf{hash}$表中寻找$B \times A^{-m \times i}(mod\ p)$,第一个就是解。
2>p不是质数
这是$EXBSGS$了,但还是说一下。
当$p$和$A$互质时,可以用欧拉定理,就是$A^{\phi(p)}\equiv 1(mod\ p)$
否则可以提$A$和$p$的公因数$d$,得到:
$A^{x-1} \times \frac{A}{d}=\frac{B}{d}(mod\ \frac{p}{d})$
如果$B \% d \neq 0$,那么就无解了。
一直提公因数直至$A$互质$p$。
$A^{x-t} \times \frac{A^t}{\prod \limits_{i}^{t} d_i}=\frac{B}{\prod \limits_{i}^{t} d_i}(mod\ \frac{p}{\prod \limits_{i}^{t} d_i})$
可以留一个坑$\lfloor\rfloor$