拥塞控制算法之Remy （2013 Sigcomm）

最近研究了一下Remy拥塞控制算法，算是在拥塞控制领域第一次采用了机器学习的方式进行速率决策。

论文题目：TCP ex Machina: Computer-Generated Congestion Control，传送门：http://nms.csail.mit.edu/papers/sigcomm13.pdf

下面直接开始写读书笔记。

核心思想：

        Remy通过一个目标函数定量判定算法的优劣程度。在生成算法的过程中，针对于不同的网络状态采取不同的方式调节发送窗口，反复修改调节方式，直到目标函数最优。最终会生成一个网络状态到调节方式的Map。在真实网络中，根据Table和网络状态，直接选取调节发送窗口的方法。

对于网络的先验假设：

       首先认为网络是一个随机生成过程，并假设其服从马尔科夫过程（未来状态只以来于当前状态）。在本文中，主要使用链路速率，传播时延和复用程度来描述网络状态，也就是网络的先验假设，本文后面设计的算法也是在服从先验假设的网络上得到的。

       但是先验假设的精确度是个比较难确定的问题，他会影响到算法性能。如果一个先验假设确定的范围非常小，设计出的算法可能针对这种网络很好，但是不具有普适性，换到不符合先验假设的网络就不好了。反之亦然。

举个栗子：就像是一个专门针对无线网络设计的算法在无线网络中会比通用算法表现好，但是在以太网中会表现得更差。

在此整理了一下比较经典的几种网络：

（1）   数据中心：网络拓扑，链路速率和最小RTT几乎可以视为已知的，但是复用程度会剧烈变动。

（2）   虚拟私网：在链路速率上会有更多的不确定性。

（3）   无线网络：复用程度不会太高，但是RTT和传输速率抖动明显。

流量模型：

       将网络中的发端建模，视为在“开”和“关”两种状态里切换。开状态时发送数据，关状态时静默。本文认为关状态的时间服从指数分布，开状态的持续时间服从经验分布（针对不同网络自行设置）。

目标函数：

       alpha-fairnessmetric评估共享链路的带宽分配情况。对于链路中不同的数据流，获得分数为：

                                                      

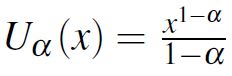
       X是该流的吞吐量，α是大于等于0的已知自己设置的值。不同的α决定公平性不一样的重要程度。所有流的分数和可以认为是该算法的得分。

       在本文中，公平性被拓展成了：

                                              

       Y是平均RTT，δ是吞吐量和时延的平衡系数，改变δ可以修改算法的侧重点。这个目标函数用来定量的刻画算法优劣。

 

发端状态的表示：

       使用三个状态变量去表示网络状态：1）收到ACK的间隔时间的指数加权移动平均，表示为ack_ewma；2）ACK中发端时间戳的间隔的指数加权移动平均，表示为send_ewma；3）当前RTT与RTT最小值的比rtt_ratio。

       在这其中，并没有考虑到丢包，一方面是因为不对丢包做出反应可以使算法更加鲁棒，另一方面是因为最大化目标函数的过程会阻止队列的累积，自然也不会出现拥塞丢包。

关于映射的描述：

        Remy的最终目的是针对不用的网络状态，做出相应的反应调节发送窗口，在此过程中，本文使用了三个参数：m是发送窗口的倍数；b是发送窗口的增量；r设定为连续发送数据包的时间间隔下限。

       所以，Remy的算法核心也就可以表示为：

                                                                               

算法生成过程：

        在Remy生成拥塞控制算法时，使用16个以上的网络样本进行评估。首先进行参数的初始化：m=b=1，r=0.01。所有的网络状态均对应为这一组参数，可以称之为action，从网络状态到action的过程可以成为一个rule。然后设定一个全局的epoch值（可以理解成迭代次数吧）为0，并开始训练算法：

（1）   设置每个rule的epoch值为当前的全局epoch值。

（2）   进行一次仿真，找到在这个epoch中最常使用的rule，

        如果存在：则找到该rule对应的action，并对m，b，r三个参数进行试探性的修改，并在完全相同的网络环境下再次进行仿真测试。如果找到了一组mbr可以获得更高的目标函数得分，则替换掉该rule中的action，并重新试探搜索更好的mbr取值，直到找不到更优的取值时，增加这一个rule的epoch值，并回到第二步。

        如果不存在：增加全局的epoch值。如果此epoch值不是K的倍数，则返回第一步继续进行。如果是K的倍数，则进行第三步。K在Remy中设置为4。

（3）细分最常用的rule。到这一步时，这个rule可以认为是网络中经常会出现的情况，所以对于描述网络状态的三个变量进行细分，产生多组相近的网络状态，并且都对应于同一个action。也就是说，从一个最常用的rule中衍生出了多组rule。在此回到第一步进行重复。

       其实这复杂的步骤可以简化描述成几个部分：首先是迭代修正action，找到最合适的一种map方法；其次就是细分最常用的rule。这样，最后就可以生成一个完整的rule table，每个rule中的action都是对当前网络状态的最优的一种调整，并且，在最常用的rule附近，划分粒度非常细，而很少出现的rule则是粗粒度的表达，这也是一种简化运算的方式。

        算法的整体描述就是这样，其实不难看出，Remy是一个非常简陋的机器学习思路，只是用在了拥塞控制领域，就发到了Sigcomm，可见现在蹭热度在学术圈也很重要啊。