游戏开发中的人工智能(四):群聚
接上文 游戏开发中的人工智能(三):移动模式
本文内容:群聚方法是 A-life 算法的实例。 A-life 算法除了可以做出效果很好的群聚行为外,也是高级群体运动的基础。
群聚
通常在游戏中,有些非玩家角色必须群聚移动,而不是个别行动。举个例子,假设你在写角色扮演游戏,在主城镇外有一片绵羊的草地,如果你的绵羊是一整群的在吃草,而不是毫无目的的在闲逛,看起来会更真实些。
这种群体行为的核心就是基本的群聚算法,本章要详谈基本群聚算法,教你如何修改算法,用来处理诸如避开障碍物之类的情况。本章接下来将以“单位”代指组成群体的个别实体,例如:绵羊、鸟、等等。
基本群聚
基本的群聚算法来自于Craig Reynolds在1987年发表的论文《Flocks,Herds and Schools:A Distributed Behavioral Model》。在论文中,他提出基本群聚算法,用以仿真整群的鸟、鱼或其他生物。
算法的三个规则:
- 凝聚:每个单位都往其邻近单位的平均位置行动。
- 对齐:每个单位行动时,都要把自己对齐在其邻近单位的平均方向上。
- 分割:每个单位行动时,要避免撞上其邻近单位。
从这三条语句可以得知,每个单位都必须有比如运用转向力行进的能力。此外,每个单位都必须得知其局部的周遭情况,必须知道邻近单位在哪里、它们的方向如何以及它们和自身有多接近。
单位视野:
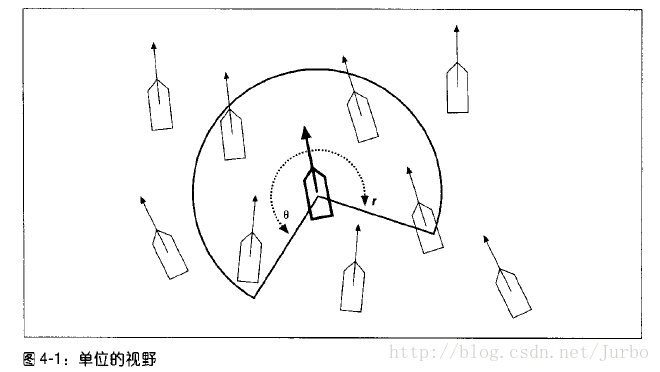
图4-1 是一个单位(图中用粗线表示的那个)以 r 为半径画弧而定出其可见视野的说明。任何其他单位落入这个弧内,都能被这个单位看见。运用群聚规则时,这些可视的单位就会有用,而其他单位都会被忽略。弧由两个参数定义:弧半径和角度 θ,这两个参数会影响最后的群聚行动。
弧半径:
较大的弧半径会让单位看到群体中更多的伙伴,从而产生更强的群体(也更多了)。也就是说,群体没有分裂成小群体的倾向,因为每个单位都可以看见多数邻近单位或全部邻近单位,再据此前进。另一方面,较小的半径会让整个群体分裂,形成较小群体的可能性较高。
角度 θ:
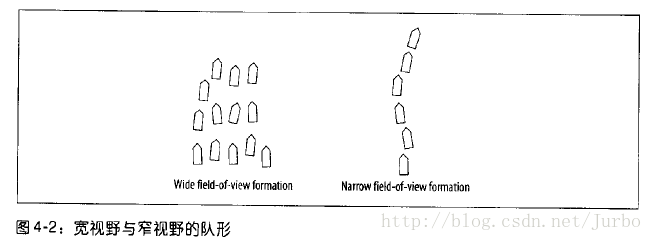
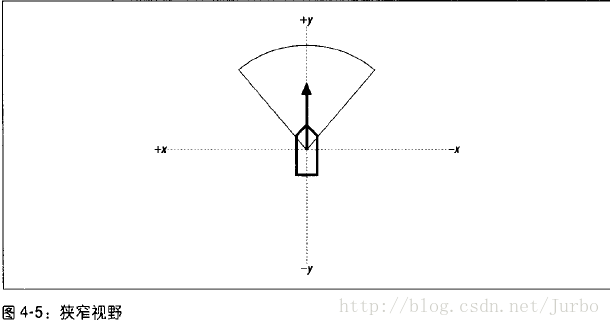
角度 θ 量定了每个单位的视野范围。最宽广的视野是360度,不过我们一般不这样做,因为这样最后得到的群聚行为可能会失真。常用的视野范围类似于图4-1 中,每个单位的身后都有一块看不见的区域。一般而言,视野宽广的话,如图4-2 左侧所示,视野角度约为270度,会得到组织良好的群体。视野较窄的话,如图4-2 右侧所示,视野角度约为45度,得到的群体像蚂蚁那样沿着单一路径行进。
宽视野和窄视野都有其作用。例如,如果你正在仿真一群喷射战机,可能会用宽视野,如果仿真一支军队鬼鬼祟祟地跟踪某人时,你也许会用窄视野,使其前后排成一条线。
群聚实例
我们打算仿真大约20个单位,以群聚的方式移动,避开圆形的物体,群聚中的诸多单位和玩家(另一个飞行器)的互动就是去追玩家。
行进模式
这个实例考虑的是以物理机制为基础的范例,把每个单位视为刚体,通过在每个单位的前端施加转向力,来保证群聚的行进模式。每条规则都会影响施加的力,最终施加的力和方向是这些规则影响的综合。另外,需要考虑两件事:首先,要控制好每条规则贡献的转向力;其次,要调整行进模式,以确保每个单位都获得平衡。
对于避开规则:为了让单位不会彼此撞上,且单位根据对齐和凝聚规则而靠在一起。当单位彼此间距离够宽时,避开规则的转向力贡献就要小一点;反之,避开规则的转向力贡献就要大一些。对于避开用的反向力,一般使用反函数就够用了,分隔距离越大,得出的避开用转向力越小;分隔距离越小,得出的避开用转向力越大。
对于对齐规则:考虑当前单位的当前方向,与其邻近单位间平均方向间的角度。如果该角度较小,我们只对其方向做小幅度调整,然而,如果角度较大,就需要较大的调整。为了完成这样的任务,可以把对齐用的转向力贡献,设定成和该单位方向及其邻近单位平均方向间的角度成正比。
邻近单位
凝聚,对齐,分隔三个规则要起作用的前提是侦测每个当前单位的邻近单位。邻近单位就是当前单位视野范围内的单位,需要从图4-1所示的视野角度和视野半径两方面进行判断。
由于群体中单位所形成的排列会随时变动,因此,游戏循环每运行一轮时,每个单位都必须更新其视野。
在示例 AIDemo4-1中,你会发现一个名为 UpdateSimulation( ) 的函数,每次走过游戏循环或仿真运算循环时,就会被调用。这个函数的责任是更新每个单位的位置并把每个单位画到画面显示缓冲区内。
例4-1 是此例的 UpdateSimulation( ) 函数。
//例4-1:UpdateSimulation()函数
void UpdateSimulation(void)
{
double dt = _TIMESTEP;
int i;
// 初始化后端缓冲区
if(FrameCounter >= _RENDER_FRAME_COUNT)
{
ClearBackBuffer();
DrawObstacles();
}
// 更新玩家控制的单位(Units[0])
Units[0].SetThrusters(false, false, 1);
Units[0].SetThrusters(false, false, 1);
if (IsKeyDown(VK_RIGHT))
Units[0].SetThrusters(true, false, 0.5);
if (IsKeyDown(VK_LEFT))
Units[0].SetThrusters(false, true, 0.5);
Units[0].UpdateBodyEuler(dt);
if(FrameCounter >= _RENDER_FRAME_COUNT)
DrawCraft(Units[0], RGB(0, 255, 0));
if(Units[0].vPosition.x > _WINWIDTH) Units[0].vPosition.x = 0;
if(Units[0].vPosition.x < 0) Units[0].vPosition.x = _WINWIDTH;
if(Units[0].vPosition.y > _WINHEIGHT) Units[0].vPosition.y = 0;
if(Units[0].vPosition.y < 0) Units[0].vPosition.y = _WINHEIGHT;
// 更新计算机控制的单位
for(i=1; i<_MAX_NUM_UNITS; i++)
{
DoUnitAI(i);
Units[i].UpdateBodyEuler(dt);
if(FrameCounter >= _RENDER_FRAME_COUNT)
{
if(Units[i].Leader)
DrawCraft(Units[i], RGB(255,0,0));
else {
if(Units[i].Interceptor)
DrawCraft(Units[i], RGB(255,0,255));
else
DrawCraft(Units[i], RGB(0,0,255));
}
}
if(Units[i].vPosition.x > _WINWIDTH) Units[i].vPosition.x = 0;
if(Units[i].vPosition.x < 0) Units[i].vPosition.x = _WINWIDTH;
if(Units[i].vPosition.y > _WINHEIGHT) Units[i].vPosition.y = 0;
if(Units[i].vPosition.y < 0) Units[i].vPosition.y = _WINHEIGHT;
}
//把后端缓冲区复制到屏幕上
if(FrameCounter >= _RENDER_FRAME_COUNT) {
CopyBackBufferToWindow();
FrameCounter = 0;
} else
FrameCounter++;
}UpdateSimulation( ) 完成的是平常的工作,清除即将绘制图像的后端缓冲区,处理玩家控制的单位的互动行为,更新计算机控制的单位,把一切都绘制进后端缓冲区,做好之后,再把后端缓冲区复制到屏幕上。UpdateSimulation( ) 会以循环走遍计算机控制单位的数组,对每个单位而言,都会调用另一个名为 DoUnitAI( ) 的函数。
DoUnitAI( ) 函数处理一切和计算机控制单位的移动有关的事。所有群聚规则都在此函数内实现。例4-2 是 DoUnitAI( ) 开头的一小部分。
//例4-2:DoUnitAI() 初始化
void DoUnitAI(int i)
{
int j;
int N; //邻近单位数量
Vector Pave; //平均位置向量
Vector Vave; //平均速度向量
Vector Fs; //总转向力
Vector Pfs; //Fs施加的位置
Vector d, u, v, w;
double m;
int Nf;
bool InView;
bool DoFlock = WideView || LimitedView || NarrowView;
int RadiusFactor;
// 初始化
Fs.x = Fs.y = Fs.z = 0;
Pave.x = Pave.y = Pave.z = 0;
Vave.x = Vave.y = Vave.z = 0;
N = 0;
Pfs.x = 0;
Pfs.y = Units[i].fLength / 2.0f;
Nf = 0;
…参数 i 代表当前正在处理的单位的数组索引值,我们要收集这个单位所有邻近单位的数据,然后再实现群聚规则。变量 j 代表 Units 数组中,其他单位的数组索引值。这些是 Units[i] 潜在的邻近单位。
N 代表邻近单位的数目,这些数目包含在当前正在处理的单位的视野内。Pave 和 Vave 分别存放的是 N 个邻近单位的平均位置和速度向量。Fs 代表施加到处理中单位的总转向力。Pfs代表转向力施加的位置,以固定于个体上的坐标表示。
d、u、v 以及 w 用来存储计算函数时的各种向量值。向量值包含全局坐标系和局部坐标系的相对位置向量和方向向量。m 是乘数变量,不是 +1 就是 -1,用来指出我们所需的转向力施加点的方向,即目前处理的单位的右侧或是左侧。
InView 是个标号,指出特定单位是否位于处理中单位的视野内。DoFlock 也是个标号,指出是否使用群聚规则。此例中,你可以打开或关闭群聚规则,也可以实现三种不同的可见视野模式,以观察群聚行为。这些可见视野模式叫做 WideView(宽广视野)、LimitedView(有限视野) 以及 NarrowView(狭窄视野)。最后,RadiusFactor 代表的是图4-1 中的 r参数(即弧半径),每种可见视野模式的 r 值都不同,而且视野角度 θ 也不同。
完成初始化后,DoUnitAI( ) 就会进入一个循环,收集当前单位周遭的邻近单位。
例4-3 是 DoUnitAI( ) 中的一端,会检查所有的邻近单位并收集数据。到此时,会进入一个循环,即 j 循环中,在这个循环里面,Units 数组的每个单位(Units[0] 除外,这是玩家控制的单位(即被追逐的单位),另外,Units[1] 也除外,这是当前单位,现在要找的是该单位的邻近单位)都会接受测试,以确认该单位是否在当前单位的视野内。如果是,其数据将被收集起来。
//例4-3:检查邻近单位并收集数据(DoUnitAI()中的一部分代码)
…
for(j=1; j<_MAX_NUM_UNITS; j++)
{
if(i!=j)
{
InView = false;
d = Units[j].vPosition - Units[i].vPosition;
w = VRotate2D(-Units[i].fOrientation, d);
if(((w.y > 0) && (fabs(w.x) < fabs(w.y)*_FRONT_VIEW_ANGLE_FACTOR)))
if(d.Magnitude() <= (Units[i].fLength * _NARROWVIEW_RADIUS_FACTOR))
Nf++;
if(WideView)
{
InView = ((w.y > 0) || ((w.y < 0) && (fabs(w.x) > fabs(w.y)*_BACK_VIEW_ANGLE_FACTOR)));
RadiusFactor = _WIDEVIEW_RADIUS_FACTOR;
}
if(LimitedView)
{
InView = (w.y > 0);
RadiusFactor = _LIMITEDVIEW_RADIUS_FACTOR;
}
if(NarrowView)
{
InView = (((w.y > 0) && (fabs(w.x) < fabs(w.y)*_FRONT_VIEW_ANGLE_FACTOR)));
RadiusFactor = _NARROWVIEW_RADIUS_FACTOR;
}
if(InView && (Units[i].Interceptor == Units[j].Interceptor))
{
if(d.Magnitude() <= (Units[i].fLength * RadiusFactor))
{
Pave += Units[j].vPosition;
Vave += Units[j].vVelocity;
N++;
}
}
…
}
}
…
确定 i 不等于 j 之后(即不检查当前的单位),这个函数会计算当前单位 Units[i] 以及 Units[j] 之间的距离向量,即两者间位置向量的差值。所得结果会存储在局部变量 d 中。接着,d 会从全局坐标转换成固定于 Units[i] 之上的局部坐标,所得结果会存储在向量 w 之中。
接着,这个函数会检查 Units[j] 是否位于 Units[i] 的视野内。这项检查是依据视野角度 θ 的检查。(我们后面也会检查 弧半径 r,但前提是视野角度 θ 的检查已经通过)
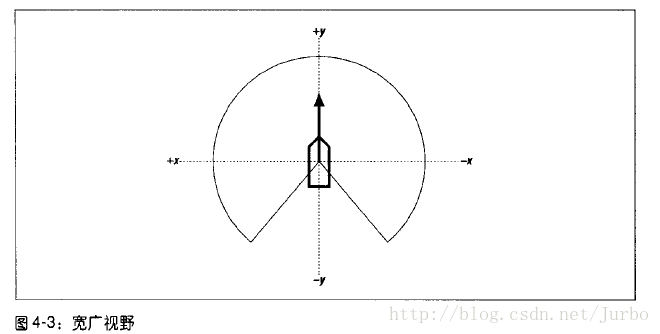
宽广视野:
例4-4:宽广视野的检查(依据视野角度θ)
//例4-4:宽广视野的检查(依据视野角度θ)
…
if(WideView)
{
InView = ((w.y > 0) || ((w.y < 0) && (fabs(w.x) > fabs(w.y)*_BACK_VIEW_ANGLE_FACTOR)));
RadiusFactor = _WIDEVIEW_RADIUS_FACTOR;
}
…在此程序代码内,_BACK_VIEW_ANGLE_FACTOR 就是视野角度系数。如果设为1,则连接视野弧线和 x 轴的夹角就是45度。如果该系数大于1,则这两条线会靠近 x 轴,相当于不可见区域比较大。相反的,如果该系数小于1,则这两条线靠近 y 轴,相当于不可见区域比较小。
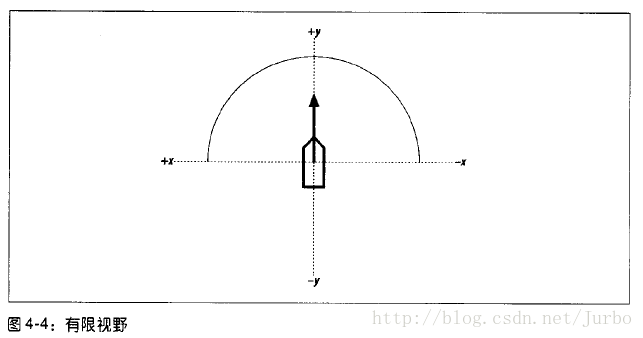
有限视野
在有限视野模式中,可见视野弧线被限制在该单位局部的+y坐标内。也就是说,每个单位都无法看到身后的任何单位。我们只需要确定,从 Units[i] 的局部坐标系来看,Units[j] 的 y 坐标是否为正值。
例4-5:有限视野的检查(依据视野角度θ)
//例4-5:有限视野的检查(依据视野角度θ)
…
if(LimitedView)
{
InView = (w.y > 0);
RadiusFactor = _LIMITEDVIEW_RADIUS_FACTOR;
}
…狭窄视野
狭窄视野把每个单位可见的范围限制在正前方。
例4-6:狭窄视野的检查(依据视野角度θ)
//例4-6:狭窄视野的检查(依据视野角度θ)
…
if(NarrowView)
{
InView = (((w.y > 0) && (fabs(w.x) < fabs(w.y)*_FRONT_VIEW_ANGLE_FACTOR)));
RadiusFactor = _NARROWVIEW_RADIUS_FACTOR;
}
…此例中,系数 _FRONT_VIEW_ANGLE_FACTOR控制了该单位前方的视野。如果此系数等于1,则构成视野锥的两条线和 x 轴的夹角就是 45度。如果系数大于1,折两条线会靠近 x 轴,也就是说可见区域比较大。如果系数小于1,则这两条线靠近 y 轴,也就是说可见区域比较小。
如果上述测试都过关了(即依据视野角度 θ 的检查已通关),那么接下来则是 依据弧半径 r 的检查。
例4-3 的最后一个 if 区块就是测试此距离。如果向量 d 的数值小于 Units[i] 的长度乘以 RadiusFactor,则表示 Units[j] 和 Units[i] 够接近。
凝聚
凝聚指的是我们想让所有单位都待在同一个群体中,我们不要每个单位和其群体分开,各走各的路。
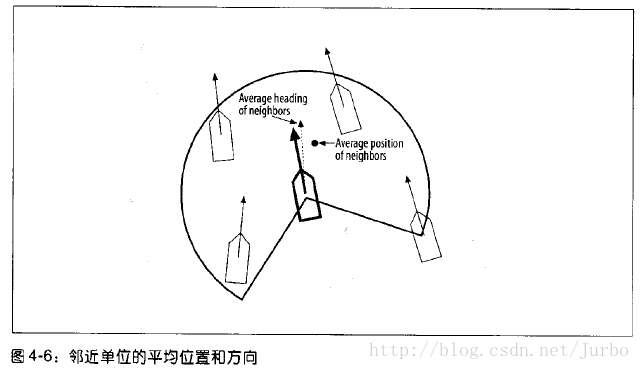
如前所述,为了满足这项规则,每个单位都应该朝其邻近单位的平均位置前进。图4-6 是某单位与其邻近单位的说明。
邻近位置的平均位置很容易计算。只要找出邻近单位后,其平均位置就是其各个位置的向量总和再除以总邻近单位数。
例4-7:邻近单位位置总和
//例4-7:邻近单位位置总和
…
if(InView && (Units[i].Interceptor == Units[j].Interceptor))
{
if(d.Magnitude() <= (Units[i].fLength * RadiusFactor))
{
Pave += Units[j].vPosition;
Vave += Units[j].vVelocity;
N++;
}
}
…Pave += Units[j].vPosition;这一行将所有邻近单位的位置向量相加。Pave 和 vPosition 是 Vector 类的变量,重载运算符会替我们做向量加法。
DoUnitAI( ) 找出邻近单位并收集信息后,就能使用群聚规则了。第一个处理的就是凝聚规则,程序代码如例4-8所示。
//4-8:凝聚规则
…
if(DoFlock && (N>0))
{
// DoFlock=true:启用凝聚规则,N>0:邻近单位数量大于零
Pave = Pave / N; // 邻近单位的平均位置向量
v = Units[i].vVelocity; // 当前单位的速度向量
v.Normalize();
u = Pave-Units[i].vPosition; // 邻近单位平均位置向量与当前单位向量的差值,相对位置向量
u.Normalize();
w.VRotate2D(-Units[i].fOrientation, u);
if(w.x < 0) m = -1; // 相对位置向量(即u)在当前单位的右边,需要右转当前单位
if(w.x > 0) m = 1; // 相对位置向量(即u)在当前单位的左边,需要左转当前单位
if(fabs(v*u) < 1) // 确保反余弦函数可以正常运行
Fs.x += m * _STEERINGFORCE * acos(v * u) / pi;
// Fs.x使用的坐标系是应该也是前面刚刚转化过的坐标系
// acos(v*u):计算相对位置向量与当前单位的速度向量之间的夹角,除以pi是为了把弧度数值转化为标量
}
…对齐
对齐的意思是指,我们想让群聚中的所有单位都大致朝相同的方向前进。为了满足这条规则,每个单位都应该在行进时,试着以等同于其邻近单位平均方向的方向来前进。
参见图4-6,中间以粗线表示的单位是沿着和其相连的粗箭头方向行进的。另外和其相连的虚箭头则代表其邻近单位的平均方向。因此,就此例而言,以粗线表示的单位必须朝右侧行进。
我们可以利用每个单位的速度向量求出其方向。把每个单位的速度向量换算成单位向量,就可以得出其方位向量。例4-7 显示出收集某单位邻近单位方向数据的过程。那一行 Vave += Units[j].vVelocity;会把每个邻近单位的速度向量累加到 Vave 中。
例4-9说明了如何计算每个单位的对齐转向力。
//例4-9:对齐规则
…
if(DoFlock && (N>0))
{
Vave = Vave / N;
u = Vave; // 邻近单位的平均速度向量
u.Normalize();
v = Units[i].vVelocity;
v.Normalize();
w.VRotate2D(-Units[i].fOrientation, u);
if(w.x < 0) m = -1;
if(w.x > 0) m = 1;
if(fabs(v*u) < 1)
Fs.x += m * _STEERINGFORCE * acos(v * u) / pi;
}
…接着,当前单位 Units[i] 的方向,可以将其速度向量换算成单位向量而求出。所得结果存储在 v 中。
分隔
分隔是指我们想让每个单位彼此间保持着最小距离,即使根据凝聚和对齐规则,它们会试着靠近一点。
因此,我们要采用分隔手段,让每个单位和其视野内的邻近单位保持某一预定的最小分隔距离。
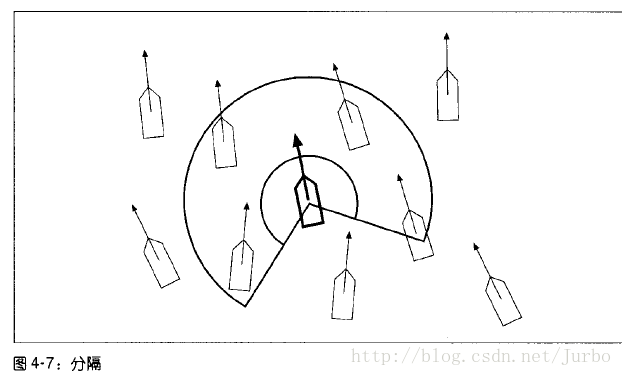
图4-7 有个单位和那个粗线表示的单位靠的太近了。以粗线表示的单位为中央的外层弧线是可见视野弧线。内层弧线代表的就是最小分隔距离。任何单位只要移动进最小分隔弧线内,则粗线表示的单位就会离它远一点。
处理分隔和处理凝聚与对齐只有一点不同,因为就分隔而言,求适当的转向力校正值时,我们必须逐一检视每个邻近单位,而不是使用所有邻近单位的某个平均值。
把分隔程序代码放在例4-3 的那个 j 循环里很方便,因为邻近单位就是在那里找出来的。需要在新的 j 循环加上分隔规则的操作程序代码,如例4-10所示。
//例4-10:邻近单位分隔
…
if(InView)
{
// 如果在视野内
if(d.Magnitude() <= Units[i].fLength * _SEPARATION_FACTOR)
{
if(w.x < 0) m = 1; // 这里是分隔,方向与凝聚和对齐规则正好相反
if(w.x > 0) m = -1;
Fs.x += m * _STEERINGFOCE * (Units[i].fLength*_SEPARATION_FACTOR) / d.Magnitude(); // 分隔越小,力越大
}
}
…避开障碍物
加入避开障碍物的行为很简单,我们要做的就是提供某种机制给那些单位使用,让他们能看到前方的障碍物,再施加适当的转向力,使其能避开路径中的障碍物。
为了检测障碍物是否在某单位的路径内,我们要借助机器人学,替我们的单位安装虚拟触角(feeler)。基本上,这些触角会处在单位的前方,如果触角碰到某种东西,就是那些单位要转向的时候了。模型的形式很多,比如可以装上三个触角,分别位于三个不同方向,不但能检测出是否有障碍物,而且检测该障碍物位于单位的那一侧。宽广的单位需要一个以上的触角,才能确保单位不会和障碍物碰撞。在3D游戏中,可以使用虚拟体积,以测定是否即将和某障碍物碰撞。
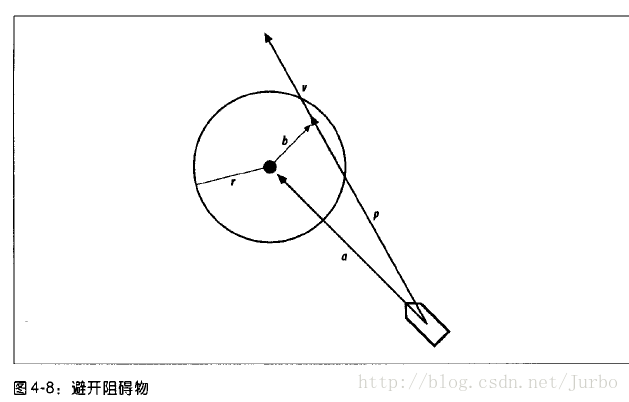
观察图4-8,可以了解我们的虚拟触角如何在几何条件下进行操作。向量 v 代表的就是触角。这个触角有某个预定的固定长度和该单位的方向在同一直线上。那个又大又暗的圆圈代表障碍物。
为了求出触角是否和障碍物在某点相交,我们得用上向量数学知识。
首先,我们计算向量 a,即该单位和障碍物位置间的差值。接着,我们取 a 和 v 的内积,将 a 投射到 v 上,可得向量 p。把向量 p 减去 向量 a,可以得到向量 b。
现在,要测试 v 是否和圆的某处相交,包含两种情况。首先,P 的数值必须小于 v 的数值。其次,b 的数值必须小于该障碍物的半径 r。如果两者都满足,则需要校正转向力,否则,该单位可以继续沿着当前方向前进。
例4-12 避开障碍物的代码 必须加进 DoUnitAI( )中,以执行避开障碍物。注意,校正的转向力也会累加在 Fs.x 成员变量中,和其他群聚规则的转向力加在一起。
例4-12:避开障碍物
…
// 避开障碍物
Vector a, p, b;
for(j=0; j<_NUM_OBSTACLES; j++)
{
u = Units[i].vVelocity;
u.Normalize();
v = u * _COLLISION_VISIBILITY_FACTOR * Units[i].fLength;
a = Obstacles[j] - Units[i].vPosition;
p = (a * u) * u;
b = p - a;
if((b.Magnitude() < _OBSTACLE_RADIUS) && (p.Magnitude() < v.Magnitude()))
{
// 即将碰撞,要避开
w = VRotate2D(-Units[i].fOrientation, a);
w.Normalize();
if(w.x < 0) m = 1;
if(w.x > 0) m = -1;
Fs.x += m * _STEERINGFORCE * (_COLLISION_VISIBILITY_FACTOR * Units[i].fLength)/a.Magnitude();
}
}
…跟随领头者
基本群聚算法的三条规则,似乎让群体在游戏世界中随处闲逛,如果在其中加入领头者,就能让群体的移动更有目的性,或者看起来比较有智能。
比如:战争模拟游戏中,计算机控制一群飞机追击玩家。可以让其中的一架作为领头者,其他飞机采用基本群聚规则跟着领头者跑。在和玩家发生混战时,可以适时关闭群聚规则,让飞机分散进攻。另一个实例,仿真一支军队,指定其中某个单位为领头者,可以让他们成横队或者纵队,采用宽广视野或有限视野模式,使其他单位采取群聚行为。
我们不会指定任何一个单位作为领头者,而是使用一些简单的规则,找出谁应该或足以担任领头者。这样一来,任何单位在任何时刻都有可能成为领头者。这种做法的好处是,当领头者被除掉,或者因为某种原因而脱离其群体时。整个群体不会因此而失去领导。
例4-13 是几行必须加进例4-3 的语句,例4-13 是求出给定单位所有邻近单位数据的程序区块。
例4-13:检查谁当领头者
…
if(((w.y > 0) && (fabs(w.x) < fabs(w.y)*_FRONT_VIEW_ANGLE_FACTOR)))
if(d.Magnitude() <= (Units[i].fLength * _NARROWVIEW_RADIUS_FACTOR))
Nf++;
…
if(InView && (Units[i].Interceptor == Units[j].Interceptor))
{
…第一个 if 区块是做检查,使用我们之前谈过的狭窄视野模式,求出当前处理单位前方视野内的单位数量。接着,这些信息将被用来确认当前单位是不是领头者。如果给定单位的前方没有其他单位,那么这个单位就是领头者,其他单位就得跟着他以群聚行为行动。如果该单位前方至少有一个单位位于其视野内,则当前单位就不是领头者,而只能遵循群聚规则行动。
第二个 if 区块是对 InView 测试做简单的修改。外加的程序代码所作的检查,是确保当前单位和 Units[j] 的类型相同,使得属于拦截者的单位和其他属于拦截者的单位一起群聚行动。而普通单位则和其他普通单位一起群聚行动。这样一来,这两种类型的单位就不会混在同一个群体中了。
因此,如果你下载了范例程序,把其中一种群聚模式打开,至少会看见两组群体:一个是普通单位的群体,另一个是拦截者(追逐着)单位构成的群体。玩家控制的单位会以绿色显示,可以用键盘方向键进行控制。
例4-14 是这两类计算机控制的单位领头者规则的操作内容
例4-14:领头者、追逐和拦截
…
// 如果该单位是领头者,就去追逐目标。Nf是当前单位前方的单位数目
if(Chase)
{
if(Nf == 0)
Units[i].Leader = true;
else
Units[i].Leader = false;
if((Units[i].Leader || !DoFlock))
{
if(!Units[i].Interceptor)
{
// 追逐
u = Units[0].vPosition;
d = u - Units[i].vPosition;
w = VRotate2D(-Units[i].fOrientation, d);
if(w.x < 0) m = -1;
if(w.x > 0) m = 1;
Fs.x += m*_STEERINGFORCE;
} else
{
// 拦截
Vector s1, s2, s12;
double tClose;
Vector Vr12;
Vr12 = Units[0].vVelocity-Units[i].vVelocity; // closing velocity
s12 = Units[0].vPosition - Units[i].vPosition; // range to close
tClose = s12.Magnitude() / Vr12.Magnitude(); // time to close
s1 = Units[0].vPosition + (Units[0].vVelocity * tClose);
Target = s1;
s2 = s1 - Units[i].vPosition;
w = VRotate2D(-Units[i].fOrientation, s2);
if(w.x < 0) m = -1;
if(w.x > 0) m = 1;
Fs.x += m*_STEERINGFORCE;
}
}
}
…如果你打开范例程序的追逐选项,则 Chase 变量会赋值为 true,而这里列出的程序区块就会被执行。在此区块内,会检查当前单位前方视野内的单位数目 Nf,以确定当前单位是否可以成为领头者。如果 Nf 为 0,则表示当前单位前方无其他单位,因此可以成为领头者。
领头者在示例中是红色显示的。
示例源代码 下载
在VC 6++ 环境下可运行。
代码:AIDemo4-1
http://pan.baidu.com/s/1hswySRi