「学习笔记」多项式的蛇皮操作

「学习笔记」多项式的蛇皮操作

写的时候注意各种数组的清空

前置知识

趋近

数学公式中，有类似于 $\leftarrow$ 或者 $\to$ 的东西，叫做趋近。

其中，前者叫做右趋近，后者叫做左趋近。

$x\to y$ 表示 $x$ 无限接近于 $y$ 同时 $x<y$ 。

$y\leftarrow x$ 表示 $x$ 无限接近于 $y$ 同时 $x>y$ 。

注意，都是严格小于/大于 而没有取等。

那么， $x\to \infty$ 叫做 $x$ 无限接近于 无限大 但同时 $x<\infty$ 。

同理， $x\to 0$ 叫做 $x$ 无限接近于 $0$ 但同时保证 $x<0$ 。

反之亦然。

自然常数

自然常数是一个叫做 $e$ 的东西，那么他是什么呢？

它的其中一个定义为 $e={\lim }_{x\to \infty }(x+\frac{1}{x}{)}^x$ 。

这个不用怎么理解，记住就好了…

对数

当满足 $a^n=x$ 时，我们定义 ${\log }_a^x=n$

在数学中，对数是对求幂的逆运算，正如除法是乘法的倒数，反之亦然。 这意味着一个数字的对数是必须产生另一个固定数字（基数）的指数。 在简单的情况下，乘数中的对数计数因子。更一般来说，乘幂允许将任何正实数提高到任何实际功率，总是产生正的结果，因此可以对于 $b$ 不等于 $1$ 的任何两个正实数 $b$ 和 $x$ 计算对数。

如果 $a$ 的 $x$ 次方等于 $N$ （ $a>0$ ，且 $a$ 不等于 $1$ ） 即 $a^x=N$ ，那么数 $x$ 叫做以 $a$ 为底 $N$ 的对数 $(logarithm)$ ，记作 $x={\log }_a^N$。其中， $a$ 叫做对数的底数， $N$ 叫做真数。

特别地，以无理数 $e$ 为底记为 $\ln$ ，称为自然对数。

逆元

这里指取模意义下的逆元。

被各种数论知识折磨过的大神们应该对这个很熟悉吧，这个就不多说了。

导函数

如果函数 $f(x)$ 在 $(a,b)$ 中每一点处都可导，则称 $f(x)$ 在 $(a,b)$ 上可导，则可建立 $f(x)$ 的导函数，简称导数，记为 $f^{\prime }(x)$ 。

看似高深莫测，实际上就是求一个函数 $f(x)$ 在 $x=x_0$ 时的 $\Delta$ 。

那么，我们有 $f^{\prime }(x)={\lim }_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$ 。

牛顿迭代与泰勒公式

这是什么？怎么全都不知道啊…

首先，牛顿迭代是基于泰勒公式的，那么我们先从泰勒公式说起：

泰勒公式是将一个在 $x=x_0$ 处具有 $n$ 阶导数的函数 $f(x)$ 利用关于 $(x-x_0)$ 的 $n$ 次多项式来逼近函数的方法。

请注意，这是是逼近，而非等于。

具体的公式呈现：

$$f(x)=\frac{f(x_0)}{0!}+\frac{f^{\prime }(x_0)}{1!}(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x)$$
对这个式子进行一些说明：

$f(x)$ ：我们要求的目标函数。

$f^{(n)}(x_0)$ ：函数 $f(x)$ 的 $n$ 阶导数。

等号后的多项式称为函数 $f(x)$ 在 $x_0$ 处的泰勒展开式，剩余的 $R_n(x)$ 是泰勒公式的余项，是 $(x-x_0)$ 的 $n$ 的高阶无穷小。

高阶无穷小：若 $\lim (\beta /\alpha )=0$ ，则称“ $\beta$ 是比 $\alpha$ 较高阶的无穷小”。意思是在某一过程 ( $x\to x_0$ 或 $x\to \infty$ 这类过程) 中， $\beta \to 0$ 比 $\alpha \to 0$ 快一些。

解释完泰勒公式，现在来说牛顿迭代…

多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。方法使用函数 $f(x)$ 的泰勒级数的前面几项来寻找方程 $f(x)=0$ 的根。

用牛顿迭代法解非线性方程，是把非线性方程 $f(x)=0$ 线性化的一种近似方法。把 $f(x)$ 在点 $x_0$ 的某邻域内展开成泰勒级数：
$$\begin{gathered} f(x)=\frac{f(x_0)}{0!}+\frac{f^{\prime }(x_0)}{1!}(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x) \\ =f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\dots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x) \end{gathered}$$

取其线性部分（即泰勒展开的前两项），并令其等于0，即
$$f(x_0)+f^{\prime }(x_0)(x-x_0)=0$$
以此作为非线性方程
$$f(x)=0$$
的近似方程，若
$$f^{\prime }(x_0)\ne 0$$
则其解为
$$x_1=x_0-\frac{f(x_0)}{f^{\prime }(x_0)}$$
这样，得到牛顿迭代法的一个迭代关系式：
$$x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$$

不定积分与定积分

积分似乎是一个很高级的东西，但是不幸的是我们现在必须了解（或者说掌握？）其基本定义与基本运算。

不定积分：在微积分中，一个函数 $f$ 的不定积分，或原函数，或反导数，是一个导数等于 $f$ 的函数 $F$ ，即 $F\prime =f$ 。

什么意思？其实就是我们根据一个导数 $f^{\prime }$ 去求一个函数 $F$ 满足 $F^{\prime }=f‘$ 。

但为什么是 不定 ？

显然，导数与函数的常数项是没有关系的，也就是说，对于一个导数 $f^{\prime }$ ，如果我们要去求其原函数 $f$ ，是求不出其原函数的 常数项 的，即常数项不定，所以我们只能退而求次，求到 $F$ （上文有解释），并称 $F$ 是 $f^{\prime }$ 的不定积分。

那么，我们就可以把这个写作
$$\int f^{\prime }=F(x)+C$$
或者
$$\int f^{\prime }(x)dx=F(x)+C$$

其中， $C$ 是任意常数。

那么，定积分是什么？

打一个比方，假如说 小明 在 $2019.1.1$ 有 $C$ 元钱，在 $2020.1.1$ 他有了 $C+\Delta$ 元钱，那么，我们可以根据作差，求到 $\Delta$ ，但是，如果我们要求到 $C$ ，似乎是不行的。

这个例子有什么用？

$C$ 就是我们上文提及的 $f$ 的常数项，是不可求的，而 $\Delta$ 是可求得，这就是定积分，是能够确定的。

并且， $\Delta$ 似乎是一个常数，也就是说：

之所以称其为定积分，是因为它积分后得出的值是确定的，是一个常数， 而不是一个函数。

定积分定义：设函数f(x) 在区间[a,b]上连续，将区间[a,b]分成n个子区间[x0,x1], (x1,x2], (x2,x3], …, (xn-1,xn]，其中x0=a，xn=b。可知各区间的长度依次是： $△x1=x1-x0$ ，在每个子区间 $(xi-1,xi]$ 中任取一点 $\xi i（1,2,...,n）$ ，作和式 ${\sum }_{i=1}^{n}f({\xi }_i)\Delta x_i$ 。该和式叫做积分和，设 $\lambda =max\{△x1,△x2,\dots ,△xn\}$ （即λ是最大的区间长度），如果当 $\lambda \to 0$ 时，积分和的极限存在，则这个极限叫做函数 $f(x)$ 在区间$[a,b]$ 的定积分，记为 ${\int }_a^{b}f(x)dx$ ，并称函数 $f(x)$ 在区间 $[a,b]$ 上可积。

接下来从几何意义上说明定积分。

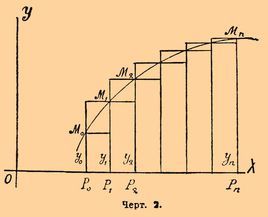
终于上图了

设图中的曲线函数为 $f(x)$ ，现在有一个定积分：
$${\int }_{P_0}^{P_1}f(x)dx$$
其表示的含义就是函数 $f(x)$ 的图像在 $P_0<x⩽P_1$ 所围出来的图形面积。

怎么求？把他们拆成很多很多个矩形，将这些矩形面积和累加，即可求得面积。

但是这样是会有误差的，但是我们发现，当 $P_0、P_1$ 越来越大，或者是越来越接近时，我们的计算就越来越精准。

---

多项式乘法

这里，我们有十分优秀的 $FFT$ 以及 $NTT$ 算法可以解决这样的问题，具体的见下面博客，这里只贴板子了…

$FFT$ 的详细解释

$NTT$ 的详细解释

时间复杂度均为 $\mathcal{O}(n\log n)$ 。

板子： $FFT$ 的模板， $NTT$ 的模板可改

class fft_task{
private:
    struct cplx{
        double vr,vi;//实部和虚部
        cplx(const double R=0,const double I=0):vr(R),vi(I){}//构造函数
        //------------------overload----------------//
        cplx operator + (const cplx a)const{return cplx(vr+a.vr,vi+a.vi);}//重载加法
        cplx operator - (const cplx a)const{return cplx(vr-a.vr,vi-a.vi);}
        cplx operator * (const cplx a)const{return cplx(vr*a.vr-vi*a.vi,vr*a.vi+a.vr*vi);}
        cplx operator / (const double var)const{return cplx(vr/var,vi/var);}
    };

    int n,m;
    cplx a[MAXN+5],b[MAXN+5];

    void fft(cplx* f,const int len,const short opt=1){
        //opt==-1 : FFT 的逆变换
        if(!len)return;
        cplx f0[len+5],f1[len+5];
        for(int i=0;i<len;++i)
            f0[i]=f[i<<1],f1[i]=f[i<<1|1];
        fft(f0,len>>1,opt);
        fft(f1,len>>1,opt);
        cplx w=cplx(cos(Pi/len),opt*sin(Pi/len)),buf=cplx(1,0);
        for(int i=0;i<len;++i,buf=buf*w){
            f[i]=f0[i]+buf*f1[i];
            f[i+len]=f0[i]-buf*f1[i];
        }
    }
public:
    inline void launch(){
        qread(n,m);
        rep(i,0,n)scanf("%lf",&a[i].vr);
        rep(i,0,m)scanf("%lf",&b[i].vr);
        for(m+=n,n=1;n<=m;n<<=1);
        fft(a,n>>1);
        fft(b,n>>1);
        rep(i,0,n-1)a[i]=a[i]*b[i];
        fft(a,n>>1,-1);
        rep(i,0,m)writc((int)((a[i].vr)/n+0.5),' ');
        Endl;
    }
}This;

---

多项式求逆元

给定一个 $A(x)$ ，求 $A^{-1}(x)$ 满足
$$A(x)A^{-1}(x)\equiv 1(\text{mod}{x}^n)$$
其中 $(\text{mod}{x}^N)$ 即为舍去次数 $⩾n$ 的项，只保留 $0$ 到 $n-1$ 次项。

而 $A^{-1}(x)$ 就是 $A(x)$ 在 $\text{mod}{x}^n$ 下的逆元。

首先，我们设 $B(x)=A^{-1}(x)$ ，那么就有
$$A(x)B(x)\equiv 1(\text{mod}{x}^n)$$
假设我们已经知道 $A(x)$ 在 $\text{mod}{x}^{\lceil \frac{n}{2}\rceil }$ 情况下的逆元 $B_0(x)$ ，那么就有
$$A(x)B_0(x)\equiv 1(\text{mod}{x}^{\lceil \frac{n}{2}\rceil })$$
而第一个式子我们也可以写为
$$A(x)B(x)\equiv 1(\text{mod}{x}^{\lceil \frac{n}{2}\rceil })$$
将这两个式子相减可得
$$A(x)(B(x)-B_0(x))\equiv 0(\text{mod}{x}^{\lceil \frac{n}{2}\rceil })$$
即
$$B(x)-B_0(x)\equiv 0(\text{mod}{x}^{\lceil \frac{n}{2}\rceil })$$
平方之后
$$B^2(x)+B_0^2(x)-2B(x)B_0(x)\equiv 0(\text{mod}{x}^n)$$
由于一个多项式平方之后，次数 $<n$ 的项至少是由原先一个次数 $<\lceil \frac{n}{2}\rceil$ 的项乘上其他项得到的，所以这个结果的 $0$ 到 $n-1$ 次系数仍然是 $0$ ，可以变成 $(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$

同乘 $A(x)$ 得
$$B(x)-2B_0(x)+A(x)B_0^2(x)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

即
$$B(x)\equiv B_0(x)(2-A(x)B_0(x))(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$
根据定义，我们可以直接取等，得
$$B(x)=B_0(x)(2-A(x)B_0(x))\text{mod}{x}^n$$
时间复杂度为
$$T(n)=T(\frac{n}{2})+\mathcal{O}(n\log n)=\mathcal{O}(n\log n)$$

题目 luoguOJ_P4238

#include
#include
using namespace std;

#define rep(i,__l,__r) for(register int i=__l,i##_end_=__r;i<=i##_end_;++i)
#define fep(i,__l,__r) for(register int i=__l,i##_end_=__r;i>=i##_end_;--i)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define ft first
#define sd second
#define LL long long
#define ull unsigned long long
#define pii pair
#define Endl putchar('\n')
// #define FILEOI
// #define int long long

#ifdef FILEOI
    #define MAXBUFFERSIZE 500000
    inline char fgetc(){
        static char buf[MAXBUFFERSIZE+5],*p1=buf,*p2=buf;
        return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXBUFFERSIZE,stdin),p1==p2)?EOF:*p1++;
    }
    #undef MAXBUFFERSIZE
    #define cg (c=fgetc())
#else
    #define cg (c=getchar())
#endif
template<class T>inline void qread(T& x){
    char c;bool f=0;
    while(cg<'0'||'9'<c)f|=(c=='-');
    for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    if(f)x=-x;
}
inline int qread(){
    int x=0;char c;bool f=0;
    while(cg<'0'||'9'<c)f|=(c=='-');
    for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    return f?-x:x;
}
template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline int gcd(const int a,const int b){return b?gcd(b,a%b):a;}
inline void getInv(int inv[],const int lim,const int MOD){
    inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
template<class T>void fwrit(const T x){
    if(x<0)return (void)(putchar('-'),fwrit(-x));
    if(x>9)fwrit(x/10);putchar(x%10^48);
}
inline LL mulMod(const LL a,const LL b,const LL mod){//long long multiplie_mod
    return ((a*b-(LL)((long double)a/mod*b+1e-8)*mod)%mod+mod)%mod;
}

inline int qkpow(int a,int n,const int mod){
    int ret=1;
    for(;n>0;n>>=1){
        if(n&1)ret=1ll*ret*a%mod;
        a=1ll*a*a%mod;
    }
    return ret;
}
inline int qkpow(int a,int n){
    int ret=1;
    for(;n>0;n>>=1){
        if(n&1)ret*=a;
        a*=a;
    }
    return ret;
}

const int MOD=998244353,g=3,gi=332748118;
const int MAXN=3e5;

int revi[MAXN+5];
inline void ntt(int* A,const int n,const short opt=1){
    rep(i,0,n-1)revi[i]=(revi[i>>1]>>1)|((i&1)?n>>1:0);
    rep(i,0,n-1)if(i<revi[i])swap(A[i],A[revi[i]]);
    for(int s=2,len,gn,Pow,tmp;s<=n;s<<=1){
        len=s>>1,gn=qkpow(opt==1?g:gi,(MOD-1)/s,MOD);
        for(int i=0;i<n;i+=s){Pow=1;
            for(int j=i;j<len+i;++j,Pow=1ll*Pow*gn%MOD){
                tmp=1ll*Pow*A[len+j]%MOD;
                A[len+j]=(0ll+A[j]-tmp+MOD)%MOD;
                A[j]=(0ll+A[j]+tmp)%MOD;
            }
        }
    }
    if(opt==-1){
        int Inv=qkpow(n,MOD-2,MOD);
        rep(i,0,n-1)A[i]=1ll*A[i]*Inv%MOD;
    }
}

int tmp[MAXN+5],p;

void polyinv(int* A,int* B,const int n){
    if(n==1)return (void)(B[0]=qkpow(A[0],MOD-2,MOD));//到了最下面, 直接取其逆元
    polyinv(A,B,(n+1)/2);//n 的上取整
    for(p=1;p<=(n<<1);p<<=1);//NTT 标准步骤
    rep(i,0,n-1)tmp[i]=A[i];//为了避免 A 数组被更改, 
    rep(i,n,p)tmp[i]=0;
    ntt(tmp,p),ntt(B,p);
    rep(i,0,p-1)B[i]=((2-1ll*B[i]*tmp[i]%MOD)%MOD+MOD)*B[i]%MOD;
    ntt(B,p,-1);
    rep(i,n,p)B[i]=0;
}

int n,A[MAXN+5],B[MAXN+5];

signed main(){
#ifdef FILEOI
    freopen("1.in","r",stdin);
    freopen("file.out","w",stdout);
#endif
    qread(n);
    rep(i,0,n-1)qread(A[i]);
    polyinv(A,B,n);
    rep(i,0,n-1)writc(B[i],' ');
    return 0;
}

---

多项式除法/取模

给定 $n-1$ 次多项式 $A(x)$ 与 $m-1$ 次多项式 $B(x)$ ，求 $D(x)、R(x)$ 满足
$$A(x)=D(x)B(x)+R(x)$$
其中 $D(x)$ 最高次项最多为 $n-m$ ， $R(x)$ 的次数 $<m-1$ 。

或者满足
$$A(x)\equiv R(x)(\mathrm{m}\mathrm{o}\mathrm{d}B(x))$$
其实，从某种角度上来说，这就是多项式除法或者是取模，取决于你想求什么。

因为有 $R(x)$ ，我们考虑将其去掉，减小问题的复杂度。

定义反转数组
$$A^R(x)=x^{n-1}A(\frac{1}{x})=\sum _{i=0}^{n-1}{a}_{n-a-i}{x}^i$$
将 $\frac{1}{x}$ 代入第一个式子，并同时乘以 $x^{n-1}$ ，可得
$$x^{n-1}A(\frac{1}{x})=x^{n-m}D(\frac{1}{x})x^{m-1}B(\frac{1}{x})+x^{n-m+1}\ast x^{m-2}R(\frac{1}{x})$$
根据反转数组的定义，可得
$$A^R(x)=D^R(x)B^R(x)+x^{n-m+1}{R}^R(x)$$
由于 $D^R(x)$ 是 $n-m$ 次的，所以其在 $(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{n-m+1})$ 下是没有影响的，那么，我们可以得到
$$A^R(x)\equiv D^R(x)B^R(x)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{n-m+1})$$
观察上式，知道 $A^R(x)、B^R(x)$ ，那么我们可以求得 $D^R(x)$ ，再通过反转得到 $D(x)$ ，即
$$A^R(x){B^R}^{-1}(x)\equiv D^R(x)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{n-m+1})$$
有一次逆元，两次乘法，时间复杂度是同样的 $\mathcal{O}(n\log n)$ 。

而 $R(x)$ 应该很好求了吧，这里不再赘述。

题目 luoguOJ_P4512

#include
#include
#include
using namespace std;

#define rep(i,__l,__r) for(register int i=__l,i##_end_=__r;i<=i##_end_;++i)
#define fep(i,__l,__r) for(register int i=__l,i##_end_=__r;i>=i##_end_;--i)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define ft first
#define sd second
#define LL long long
#define ull unsigned long long
#define pii pair
#define Endl putchar('\n')
// #define FILEOI
// #define int long long

#ifdef FILEOI
    #define MAXBUFFERSIZE 500000
    inline char fgetc(){
        static char buf[MAXBUFFERSIZE+5],*p1=buf,*p2=buf;
        return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXBUFFERSIZE,stdin),p1==p2)?EOF:*p1++;
    }
    #undef MAXBUFFERSIZE
    #define cg (c=fgetc())
#else
    #define cg (c=getchar())
#endif
template<class T>inline void qread(T& x){
    char c;bool f=0;
    while(cg<'0'||'9'<c)f|=(c=='-');
    for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    if(f)x=-x;
}
inline int qread(){
    int x=0;char c;bool f=0;
    while(cg<'0'||'9'<c)f|=(c=='-');
    for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    return f?-x:x;
}
template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline int gcd(const int a,const int b){return b?gcd(b,a%b):a;}
inline void getInv(int inv[],const int lim,const int MOD){
    inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
template<class T>void fwrit(const T x){
    if(x<0)return (void)(putchar('-'),fwrit(-x));
    if(x>9)fwrit(x/10);putchar(x%10^48);
}
inline LL mulMod(const LL a,const LL b,const LL mod){//long long multiplie_mod
    return ((a*b-(LL)((long double)a/mod*b+1e-8)*mod)%mod+mod)%mod;
}

inline int qkpow(int a,int n,const int mod){
    int ret=1;
    for(;n>0;n>>=1){
        if(n&1)ret=1ll*ret*a%mod;
        a=1ll*a*a%mod;
    }
    return ret;
}
inline int qkpow(int a,int n){
    int ret=1;
    for(;n>0;n>>=1){
        if(n&1)ret*=a;
        a*=a;
    }
    return ret;
}

const int MOD=998244353,g=3,gi=332748118;
const int MAXN=3e5;

int revi[MAXN+5];
inline void ntt(int* A,const int n,const short opt=1){
    rep(i,0,n-1)revi[i]=(revi[i>>1]>>1)|((i&1)?n>>1:0);
    rep(i,0,n-1)if(i<revi[i])swap(A[i],A[revi[i]]);
    for(int s=2,len,gn,Pow,tmp;s<=n;s<<=1){
        len=s>>1,gn=qkpow(opt==1?g:gi,(MOD-1)/s,MOD);
        for(int i=0;i<n;i+=s){Pow=1;
            for(int j=i;j<len+i;++j,Pow=1ll*Pow*gn%MOD){
                tmp=1ll*Pow*A[len+j]%MOD;
                A[len+j]=(0ll+A[j]-tmp+MOD)%MOD;
                A[j]=(0ll+A[j]+tmp)%MOD;
            }
        }
    }
    if(opt==-1){
        int Inv=qkpow(n,MOD-2,MOD);
        rep(i,0,n-1)A[i]=1ll*A[i]*Inv%MOD;
    }
}

int tmp[MAXN+5];
void polyinv(int* A,int* B,const int n){
    if(n==1)return (void)(B[0]=qkpow(A[0],MOD-2,MOD));//到了最下面, 直接取其逆元
    polyinv(A,B,(n+1)/2);//n 的上取整
    int p;
    for(p=1;p<=(n<<1);p<<=1);//NTT 标准步骤
    rep(i,0,n-1)tmp[i]=A[i];//为了避免 A 数组被更改
    rep(i,n,p)tmp[i]=0;
    ntt(tmp,p),ntt(B,p);
    rep(i,0,p-1)B[i]=((2-1ll*B[i]*tmp[i]%MOD)%MOD+MOD)*B[i]%MOD;
    ntt(B,p,-1);
    rep(i,n,p)B[i]=0;
}

int Ar[MAXN+5],Br[MAXN+5],Br_[MAXN+5];
inline void polydiv(int* A,int* B,int* D,int* R,int n,int m){
    memset(Ar,0,sizeof Ar);memset(Br,0,sizeof Br);memset(Br_,0,sizeof Br_);
    rep(i,0,n-1)Ar[i]=A[n-i-1];
    rep(i,0,m-1)Br[i]=B[m-i-1];
    polyinv(Br,Br_,n-m+1);
    int p;
    for(p=1;p<=n*2-m+1;p<<=1);
    /*
        因为 Br(x) 的逆元 Br_(x) 是在 mod x^{n-m+1} 的情况下进行的
        因而其长度为 n-m+1
        再加上 A(x) 的长度 n
        总长即为 n+n-m+1=n*2-m+1
    */
    ntt(Ar,p),ntt(Br_,p);
    rep(i,0,p-1)D[i]=1ll*Ar[i]*Br_[i]%MOD;
    ntt(D,p,-1);
    rep(i,n-m+1,p)D[i]=0;//因为 D(x) 的最高次为 n-m , 因而后面的都可以全部清零
    for(int i=0,j=n-m;i<j;++i,--j)swap(D[i],D[j]);//求得 Dr(x) , 还需反转

    for(p=1;p<=n;p<<=1);
    /*
        n+1=n-m+m
        n-m : 多项式 D
        m : 多项式 B
    */
    rep(i,0,m-1)Br[i]=B[i];rep(i,m,p)Br[i]=0;
    rep(i,0,n-m)Br_[i]=D[i];rep(i,n-m+1,p)Br_[i]=0;
    ntt(Br,p),ntt(Br_,p);
    rep(i,0,p-1)R[i]=1ll*Br[i]*Br_[i]%MOD;
    ntt(R,p,-1);
    rep(i,0,n-1)R[i]=(0ll+A[i]-R[i]+MOD)%MOD;
}

int n,m,F[MAXN+5],G[MAXN+5],Q[MAXN+5],R[MAXN+5];

signed main(){
#ifdef FILEOI
    freopen("1.in","r",stdin);
    freopen("file.out","w",stdout);
#endif
    qread(n,m);
    rep(i,0,n)qread(F[i]);
    rep(i,0,m)qread(G[i]);
    polydiv(F,G,Q,R,n+1,m+1);
    rep(i,0,n-m)printf("%d ",Q[i]);
    Endl;
    rep(i,0,m-1)printf("%d ",R[i]);
    Endl;
    return 0;
}

---

多项式牛顿迭代法

这个部分没有代码，只是一种思想。

有一个关于多项式 $f(x)$ 的方程 $d(f(x))=0$

对 $g(f(x))$ 的说明（如果理解其含义可直接跳过）：

这里的 $f(x)$ 并非是一个值，而是多项式，比如有
$$g(x)=4x^2+1$$
并且我们令
$$f(x)=x+4$$
那么，就有
$$g(f(x))=4(x+4{)}^2+1$$

现在开始说明牛顿迭代法。

假设我们已经知道了 $f(x)$ 的前 $n$ 项的多项式 $f_0(x)$ ，即
$$\begin{gathered} f(x)\equiv f_0(x)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n) \\ g(f_0(x))\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n) \end{gathered}$$
然后，我们对 $g(f(x))$ 在 $f_0(x)$ 上进行泰勒展开
$$g(f(x))=g(f_0(x))+\frac{g^{\prime }(f_0(x))}{1!}(f(x)-f_0(x){)}^1+\frac{g^{\prime \prime }{f}_0(x)}{2!}(f(x)-f_0(x){)}^2+\dots \dots$$
根据定义，有 $f(x)-f_0(x)$ 的前 $n$ 项系数为 $0$ ，那么就有
$$g(f(x))\equiv g(f_0(x))+g^{\prime }(f_0(x))(f(x)-f_0(x))\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{2n})$$
即
$$f(x)\equiv f_0(x)-\frac{g(f_0(x))}{g^{\prime }(f_0(x))}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{2n})$$

用这种方法也可以推多项式求逆。

多项式开根

给定多项式 $A(x)$ ，求 $B(x)$ 使得
$$B^2(x)-A(x)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$
设 $B(x)\equiv B_0(x)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$ ，换句话说，设 $B(x)$ 与 $B_0(x)$ 的前 $n$ 项相同。

再令 $g(x)=B_0^2(x)-A(x)$ ，那么其导函数 $g^{\prime }(x)=2B_0(x)$ 。

这与牛顿迭代的定义相似，那么直接带入牛顿迭代，可得
$$\begin{array}{rl}B(x)& \equiv B_0(x)-\frac{B_0^2(x)-A(x)}{2B_0(x)}\\ & \equiv \frac{1}{2}\left(B_0(x)+\frac{A(x)}{B_0(x)}\right)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{2n})\end{array}$$
这样，我们也可以考虑用类似于倍增的思想。

时间复杂度 $\mathcal{O}(n\log n)$ 。

说明：牛顿迭代不是 逼近 吗？怎么可以拿来求根，万一不精准呢？

我们想一个问题，在我们普通的一些求根之中，不可能也算到精准吧？

比如 $\sqrt{2}=1.414...$ 而我们一般都取 $1.414$ 等等。

多项式也是如此