浅谈权值线段树

#简介

线段树大家都知道，不知道的话点这里。我们线段树是以标号为关键字的线段树，顾名思义，权值线段树就是以权值为关键字的一棵线段树。其实在实现的时候，比线段树还简单，如果你真正理解了线段树的话~~权值线段树一般是用来快速求一个区间的第k大（或小），如果你会splay的话请自动点×。

#工作原理
权值线段树是用来求第k大（或小的）。假设我们由一串数：1,5,2,7,4,6。要你求每次按照顺序插入一个数，求当前的第3小，这样的题目我们就可以用权值线段树了。假设，我们现在先加入1：

我们就在权值为1的那个点上面加上一，表示它出现了一次。
再加入5:

就又在权值为5的地方加上一，表示它也出现了一次。
然后再看看全部都加进去的情况：
这就是全部都放进去…
假设，我们在7刚放进去的时候找第3小，就是这样的情景：

首先，我们在根节点，向下去找第3大：
发现我们左边只有两个数，那么第三大肯定在右边，那我们就走右边：
然后，我们就要减去左边的2，就表示我们本来第三小，现在在右边找最小的就好了。
那么，就知道，当前的左儿子就有一个，那么刚好满足条件，就进去，我们就找到啦！！
答案就是5啦！
是不是很有味道，其实实现起来也不难。
我们那一道例题吧！
#例题
#黑匣子
Description
Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量 i 。最开始的时候Black Box是空的，而 i 等于 0。这个 Black Box 要处理一串命令。
命令只有两种：
ADD(x): 把 x 元素放进 Black Box;
GET: i 加 1 ，然后输出 Black box 中第 i 小的数。
记住：第 i 小的数，就是 Black Box里的数的按从小到大的顺序排序后的第 i 个元素。
例如
我们来演示一下一个有11个命令的命令串。

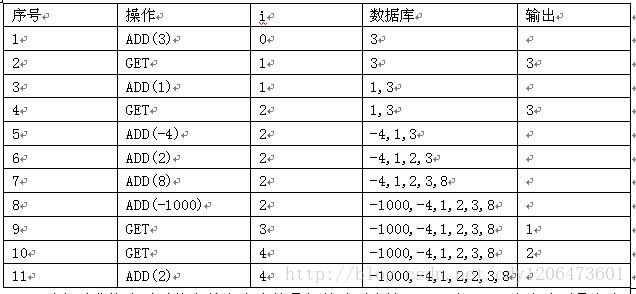
现在要求找出对于给定的命令串的最好的处理方法。ADD 和 GET 命令分别最多有200000个。
现在用两个整数数组来表示命令串：

1. A(1), A(2), …, A(M): 一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M <=200000。例如上面的例子就是A=(3, 1, -4, 2, 8, -1000, 2).
2. u(1), u(2), …, u(N): 表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(1, 2, 6, 6)。 输入数据不用判错。
   Input
   第一行，两个整数，M，N，
   第二行，M个整数，表示A(1)……A(M)，
   第三行，N个整数，表示u(1)……u(N)。
   Output
   输出 Black Box 根据命令串所得出的输出串，一个数字一行。
   Sample Input
   7 4
   3 1 -4 2 8 -1000 2
   1 2 6 6
   Sample Output
   3
   3
   1
   2
   Data Constraint
   【数据规模】
   对于30%的数据，M<=10000；
   对于50%的数据，M<=100000；
   对于100%的数据，M<=200000。
   这道题其实就是一道裸的权值线段树，我不多说了，自己看看标程吧！

var
        a,b,al,bz,wz,wz1:array[0..200000]of longint;
        f,fy:array[0..262129]of longint;
        n,i,t,m,nn,j,k,len:longint;
procedure kp(l,r:longint);
var
        i,j,mid:longint;
begin
        i:=l;
        j:=r;
        mid:=a[l];
        while i<=j do
        begin
                while a[i]mid do dec(j);
                if i<=j then
                begin
                        a[0]:=a[i];
                        a[i]:=a[j];
                        a[j]:=a[0];
                        wz[0]:=wz[i];
                        wz[i]:=wz[j];
                        wz[j]:=wz[0];
                        inc(i);
                        dec(j);
                end;
        end;
        if li then kp(i,r);
end;
procedure make(v,l,r,x:longint);
var
        mid:longint;
begin
        mid:=(l+r) div 2;
        if l=r then
        begin
                inc(f[v]);
                fy[v]:=a[bz[l]];
                exit;
        end
        else
        begin
                if x<=mid then make(v*2,l,mid,x);
                if x>mid then make(v*2+1,mid+1,r,x);
        end;
        f[v]:=f[v*2]+f[v*2+1];
end;
function find(v,l,r,k:longint):longint;
var
        mid:longint;
begin
        mid:=(l+r) div 2;
        if l=r then exit(fy[v])
        else
        begin
                if k<=f[v*2] then exit(find(v*2,l,mid,k));
                if k>f[v*2] then exit(find(v*2+1,mid+1,r,k-f[v*2]));
        end;
        f[v]:=f[v*2]+f[v*2+1];
end;
begin
        readln(n,m);
        for i:=1 to n do
        begin
                read(a[i]);
                wz[i]:=i;
        end;
        for i:=1 to m do
                read(b[i]);
        kp(1,n);
        j:=0;
        for i:=1 to n do
                if a[i]<>a[i-1] then
                begin
                        inc(j);
                        al[i]:=j;
                        bz[j]:=i;
                        wz1[wz[i]]:=i;
                end
                else
                begin
                        al[i]:=al[i-1];
                        wz1[wz[i]]:=i;
                end;
        len:=j;
        j:=1;
        k:=0;
        for i:=1 to n do
        begin
                make(1,1,len,al[wz1[i]]);
                while b[j]=i do
                begin
                        inc(k);
                        inc(j);
                        writeln(find(1,1,len,k));
                end;
        end;
end.