机器学习练习项目(决策树):泰坦尼克号乘客生还率预测
相应的数据集和可执行文件均可以在本文中获取。以下各段代码也均可在jupyter中运行,可以随时查看结果。
题目描述:
1912年,泰坦尼克号在第一次航行中就与冰山相撞沉没,导致了大部分乘客和船员身亡。在这个项目中,我们将探索部分泰坦尼克号旅客名单,来确定哪些特征可以最好地预测一个人是否会生还。
分析数据
import numpy as np #导入包
import pandas as pd
# 加载数据集
full_data = pd.read_csv('titanic_data.csv')
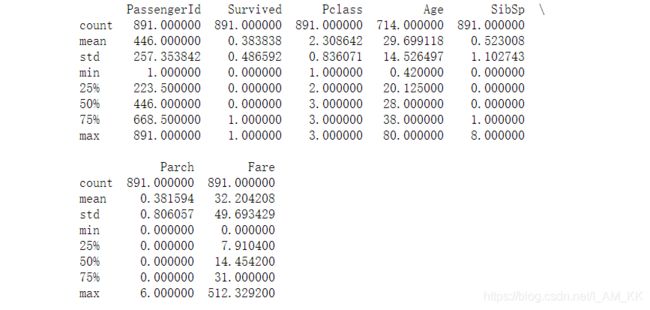
print(full_data.describe()) #打印数据集
- count:总数
- mean:平均值
- std:是方差
- min:最小值
- 25%、50%、75%:位于总数据分别为25%、50%、75%的数据
- max:最大值
表中每列是数据里面旅客的特征:
- PassengerId:乘客ID
- Survived:是否存活(0代表否,1代表是)
- Pclass:社会阶级(1代表上层阶级,2代表中层阶级,3代表底层阶级)
- Age:船上乘客的年龄(可能存在 NaN)
- SibSp:乘客在船上的兄弟姐妹和配偶的数量
- Parch:乘客在船上的父母以及小孩的数量
- Fare:乘客为船票支付的费用
这和我们直接在csv表里面看到的数据不一样,那是因为打印的时候没有处理字符列。
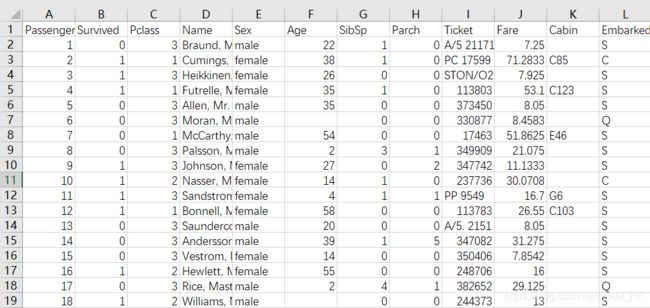
- Survived:是否存活(0代表否,1代表是)
- Pclass:社会阶级(1代表上层阶级,2代表中层阶级,3代表底层阶级)
- Name:船上乘客的名字
- Sex:船上乘客的性别
- Age:船上乘客的年龄(可能存在
NaN) - SibSp:乘客在船上的兄弟姐妹和配偶的数量
- Parch:乘客在船上的父母以及小孩的数量
- Ticket:乘客船票的编号
- Fare:乘客为船票支付的费用
- Cabin:乘客所在船舱的编号(可能存在
NaN) - Embarked:乘客上船的港口(C 代表从 Cherbourg 登船,Q 代表从 Queenstown 登船,S 代表从 Southampton 登船)
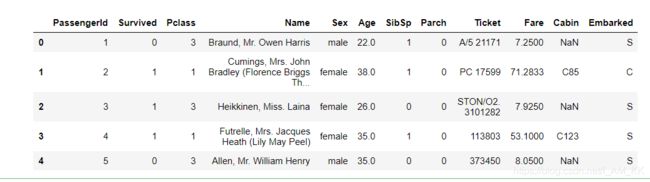
我们单独把数据集的前几行打印出来看下
display(full_data.head())#显示前5行
从上面这些表中可以看到年龄(Age)列只有714行,缺失了105行。所以我们要对缺失值进行处理。
考虑到年龄最小值是0.42,最大值80,这里用中位数填充缺失值,因为中位数不受极端变量值的影响。
# 年龄缺失值处理
full_data['Age']=full_data['Age'].fillna( full_data['Age'].median())# 用中位数填充
# 再次查看数据完整性
print(full_data.describe())
因为我们感兴趣的是每个乘客或船员是否在事故中活了下来。可以将 Survived 这一特征从这个数据集移除,并且用一个单独的变量 outcomes 来存储。它也做为我们要预测的目标。
# 从数据集中移除 'Survived' 这个特征,并将它存储在一个新的变量中。
outcomes = full_data['Survived']
data = full_data.drop('Survived', axis = 1)
# 显示已移除 'Survived' 特征的数据集前5行
display(data.head())
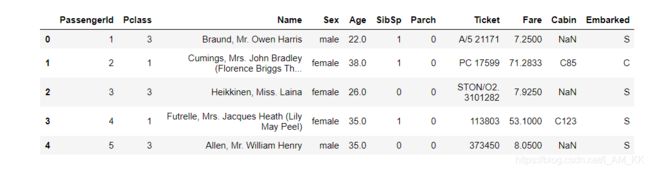
此时泰坦尼克号的 Survived 数据从 DataFrame 移除。 data(乘客数据)和 outcomes (是否存活)现在已经匹配好。也就是对于任何乘客的 data.loc[i] 都有对应的存活的结果 outcome[i]。
定义评判标准(计算准确率)
为了验证我们预测的结果,我们需要一个标准来给我们的预测打分。预测的准确率,既正确预测乘客存活的比例。
创建我们的 accuracy_score 函数以对前五名乘客的预测来做测试。
假设预测他们全部都存活,求预测的准确率。
def accuracy_score(truth, pred):
# 确保预测的数量与结果的数量一致
if len(truth) == len(pred):
# 计算预测准确率(百分比)
return "Predictions have an accuracy of {:.2f}%.".format((truth == pred).mean()*100)
else:
return "Number of predictions does not match number of outcomes!"
# 测试 'accuracy_score' 函数
predictions = pd.Series(np.ones(5, dtype = int)) #把五个人的生存都置为1,既存活
print(accuracy_score(outcomes[:5], predictions))#打印准确率
Predictions have an accuracy of 60.00%.
假设所有人都遇难了,求此时的准确率
def predictions_0(data):
predictions = []
for _, passenger in data.iterrows():#遍历总数据的个数
# 把所有人的生存都置为0
predictions.append(0)
# 返回设定好的遇难结果
return pd.Series(predictions)
# 进行预测
predictions = predictions_0(data)#传入当前数据
print (accuracy_score(outcomes, predictions))#打印准确率
Predictions have an accuracy of 61.62%.
以上的测试完毕
考虑使用一个特征进行预测
我们来看看 Sex 这一特征对乘客的存活率有多大影响。
运行下面的代码绘制出依据乘客性别计算存活率的柱形图。
import matplotlib.pyplot as plt
# Merge data and outcomes into single dataframe
all_data = pd.concat([data, outcomes], axis = 1)
# Create outcomes DataFrame
all_data = all_data[['Sex', 'Survived']]
# Create plotting figure
plt.figure(figsize=(8,6))
values = ['male', 'female']
frame = pd.DataFrame(index = np.arange(len(values)), columns=('Sex','Survived','NSurvived'))
for i, value in enumerate(values):
frame.loc[i] = [value, \
len(all_data[(all_data['Survived'] == 1) & (all_data['Sex'] == value)]), \
len(all_data[(all_data['Survived'] == 0) & (all_data['Sex'] == value)])]
# Set the width of each bar
bar_width = 0.4
# Display each category's survival rates
for i in np.arange(len(frame)):
nonsurv_bar = plt.bar(i-bar_width, frame.loc[i]['NSurvived'], width = bar_width, color = 'r')
surv_bar = plt.bar(i, frame.loc[i]['Survived'], width = bar_width, color = 'g')
plt.xticks(np.arange(len(frame)), values)
plt.legend((nonsurv_bar[0], surv_bar[0]),('Did not survive', 'Survived'), framealpha = 0.8)
# Common attributes for plot formatting
plt.xlabel('Sex')
plt.ylabel('Number of Passengers')
plt.title('Passenger Survival Statistics With \'%s\' Feature'%('Sex'))
plt.show()
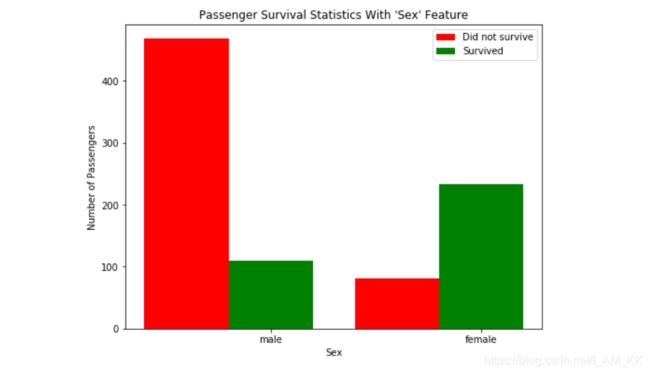
观察泰坦尼克号上乘客存活的数据统计,我们可以发现大部分男性乘客在船沉没的时候都遇难了。相反的,大部分女性乘客都在事故中生还。让我们以此改进先前的预测:如果乘客是男性,那么我们就预测他们遇难;如果乘客是女性,那么我们预测他们在事故中活了下来。
用访问 dictionary(字典)的方法来访问船上乘客的每个特征对应的值。例如, passenger['Sex'] 返回乘客的性别,并计算准确率。
def predictions_1(data):
""" 只考虑一个特征,如果是女性则生还 """
predictions = []
for _, passenger in data.iterrows():
# 输入预测条件
if passenger['Sex'] == 'female':
predictions.append(1)
else:
predictions.append(0)
# 返回预测结果
return pd.Series(predictions)
# 进行预测
predictions = predictions_1(data)
#打印准确率
print (accuracy_score(outcomes, predictions))
Predictions have an accuracy of 78.68%.
当我们预测船上女性乘客全部存活,而剩下的人全部遇难,那么我们预测的准确率是78.68%.
考虑两个特征进行预测
仅仅使用乘客性别(Sex)这一特征,我们预测的准确性就有了明显的提高。现在再看一下使用额外的特征能否更进一步提升我们的预测准确度。例如,综合考虑所有在泰坦尼克号上的男性乘客:我们是否找到这些乘客中的一个子集,他们的存活概率较高。我们来看看每位男性乘客的年龄(Age)。
下面这段代码,把男性基于年龄的生存结果绘制出来。
#保存性别为男性的数据
all_data = pd.concat([data, outcomes], axis = 1)
all_data = all_data[all_data['Sex'] == 'male']
all_data = all_data[['Age', 'Survived']]
# Divide the range of data into bins and count survival rates
min_value = all_data['Age'].min()
max_value = all_data['Age'].max()
value_range = max_value - min_value
bins = np.arange(0, all_data['Age'].max() + 10, 10)
# Overlay each bin's survival rates
nonsurv_vals = all_data[all_data['Survived'] == 0]['Age'].reset_index(drop = True)
surv_vals = all_data[all_data['Survived'] == 1]['Age'].reset_index(drop = True)
plt.hist(nonsurv_vals, bins = bins, alpha = 0.6,
color = 'red', label = 'Did not survive')
plt.hist(surv_vals, bins = bins, alpha = 0.6,
color = 'green', label = 'Survived')
# Add legend to plot
plt.xlim(0, bins.max())
plt.legend(framealpha = 0.8)
# Common attributes for plot formatting
plt.xlabel('Age')
plt.ylabel('Number of Passengers')
plt.title('Passenger Survival Statistics With \'%s\' Feature'%('Age'))
plt.show()

仔细观察泰坦尼克号存活的数据统计,在船沉没的时候,大部分小于10岁的男孩都活着,而大多数10岁以上的男性都随着船的沉没而遇难。让我们继续在先前预测的基础上构建:如果乘客是女性,那么我们就预测她们全部存活;如果乘客是男性并且小于10岁,我们也会预测他们全部存活;所有其它我们就预测他们都没有幸存。
用之前 predictions_1 的代码作为开始来修改代码,实现新的预测函数predictions_2。
def predictions_2(data):
""" 考虑两个特征:
- 如果是女性则生还
- 如果是男性并且小于10岁则生还 """
predictions = []
for _, passenger in data.iterrows():
if passenger['Sex'] == 'female':
predictions.append(1)
else:
if passenger['Age'] < 10:
predictions.append(1)
else:
predictions.append(0)
# 返回预测结果
return pd.Series(predictions)
# 进行预测
predictions = predictions_2(data)
print(accuracy_score(outcomes, predictions))
Predictions have an accuracy of 79.35%.
当预测所有女性以及小于10岁的男性都存活的时候,预测的准确率会达到79.35%。
添加年龄(Age)特征与性别(Sex)的结合比单独使用性别(Sex)也提高了不少准确度。
考虑多个特征进行预测
在不同的条件下多次使用相同的特征,使得预测结果提高到80%以上。
def predictions_3(data):
predictions = []
for _, passenger in data.iterrows():
# 输入你自己的预测条件
if passenger['Sex'] == 'female':
predictions.append(1)
else:
if passenger['Age'] < 10:
predictions.append(1)
else:
if passenger['Fare']>=90 :
predictions.append(1)
else:
predictions.append(0)
# 返回预测结果
return pd.Series(predictions)
# 进行预测
predictions = predictions_3(data)
print(accuracy_score(outcomes, predictions))
Predictions have an accuracy of 78.79%.
结论
经过了数次对数据的探索和分类,创建了一个预测泰坦尼克号乘客存活率的有用的算法。在这个项目中我们手动地实现了一个简单的机器学习模型——决策树(decision tree)。决策树每次按照一个特征把数据分割成越来越小的群组(被称为 nodes)。每次数据的一个子集被分出来,如果分割后新子集之间的相似度比分割前更高(包含近似的标签),我们的预测也就更加准确。电脑来帮助我们做这件事会比手动做更彻底,更精确。这个链接提供了另一个使用决策树做机器学习入门的例子。
决策树是许多监督学习算法中的一种。在监督学习中,我们关心的是使用数据的特征并根据数据的结果标签进行预测或建模。也就是说,每一组数据都有一个真正的结果值,不论是像泰坦尼克号生存数据集一样的标签,或者是连续的房价预测。