LeetCode 940 解题思路
这道题是随机选的,看了看题目,刚好和前段时间看了MIT6.00课程中的Dynamic Programming很像,于是就想着去解决试试。没找到Dynamic Programming在这里的切入点,运算结果是对的(报:Time Limit Exceeded),就是计算复杂度太高了——![]() ,当然十分惨烈。
,当然十分惨烈。
940. Distinct Subsequences II
Given a string
S, count the number of distinct, non-empty subsequences ofS.Since the result may be large, return the answer modulo
10^9 + 7.Example 1:
Input: "abc" Output: 7 Explanation: The 7 distinct subsequences are "a", "b", "c", "ab", "ac", "bc", and "abc".Example 2:
Input: "aba" Output: 6 Explanation: The 6 distinct subsequences are "a", "b", "ab", "ba", "aa" and "aba".Example 3:
Input: "aaa" Output: 3 Explanation: The 3 distinct subsequences are "a", "aa" and "aaa".
1. 直接求解
首先用的是课程中介绍的,结合递归方法和二叉树,对所有结果进行遍历(穷举法,又一次用上了Brute Force)。往树的左边不选当前字符,往树的右边就选一个字符,一直递归下去就可以获得所有的结果。结果集中包括空字符和重复的,因此选用Set进行过滤,得到不重复的结果,可以时间复杂度太高,在LeetCode中的时候计算超时了。
sub_set = set()
def get_sub_set(left_str, S):
if len(S) == 0:
print left_str
sub_set.add(left_str)
return
# print S
not_pick_one = left_str
get_sub_set(not_pick_one, S[1:])
# print 'notPick', pick_left
pick_one = left_str + S[0]
# print 'pick', pick_one
get_sub_set(pick_one, S[1:])
def distinctSubseqII(S):
"""
:type S: str
:rtype: int
"""
get_sub_set('', S)
return len(sub_set) - 1
def test():
s1 = 'abc'
print (7, distinctSubseqII(s1))
s1 = 'aba'
print (6, distinctSubseqII(s1))
s1 = 'aaa'
print (3, distinctSubseqII(s1))
test()2. Dynamic Programming
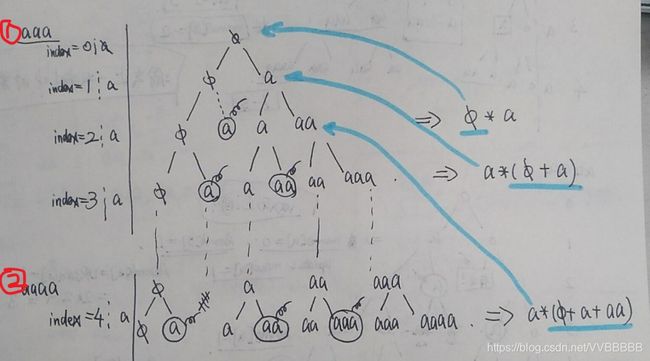
昨天想了很久,没想明白,睡觉的时候突然想起来,为什么结合前面二叉树的分布,来进行可视化操作呢?于是,在又经历了近2小时,总于想透了,如下图所示。
---
这里有两个假设
①在生成当前层字符时,所有来自上一层的字符都放在节点的左侧。
②在生成当前层字符时,新生成的字符放在节点的右侧。因此只需考虑新节点是否和之前的子字符重合即可。
我们需获取字符‘aaa’的所有子字符串,按以下步骤
- index=0时,为——空:
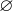
- index=1时,为——
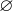 ,a
,a - index=2时,为——
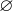 ,a,a,aa。但由于以前的经验(当前字符都是在以前字符的基础上生成),我们知道从index=0的
,a,a,aa。但由于以前的经验(当前字符都是在以前字符的基础上生成),我们知道从index=0的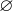 中派生,会有结果
中派生,会有结果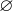 ,a。而index=1中,也有一个
,a。而index=1中,也有一个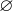 ,并要进行向右派生。但此时不就和index=0中的情形重合了吗?于是要删去。最终结果为:
,并要进行向右派生。但此时不就和index=0中的情形重合了吗?于是要删去。最终结果为: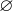 ,a,aa
,a,aa - index=3时,同理,可以过滤掉重复的结果a,aa,得到
 ,a,aa,aaa
,a,aa,aaa
当我们要去求‘aaaa’的所有子字符串呢?以上步骤1-4不变,来看第五步,index=3的结果,直接继承到树的左侧,现在只关注即将生成新结果的树右侧。本来index=3的结果产生来自于index=2,因此只需要去除此部分达到了去重的效果。
若在字符中混入了不同了字符,则判别方法类似,只需要找到同一个字符在上一个位置,并去除重复的数量即可——这里包含的思想其实是分而治之。
解决方法如下,解决方法来自这个Discusss:
def distinctSubseqII(S):
"""
:type S: str
:rtype: int
"""
memo = {S[0]: 0}
dp = [0] + [0]*len(S)
dp[0] = 1
dp[1] = 2
mode_val = 10**9+7
for index in range(1, len(S)):
word = S[index]
# print index, 'word:', word
if word not in memo:
dp[index+1] = (2 * dp[index] % mode_val)
else:
# print memo[word]
value = 2 * dp[index] - dp[memo[word]]
dp[index+1] = value % mode_val
memo[word] = index
# print dp
return dp[-1] - 1
def test():
s1 = 'abc'
print (7, distinctSubseqII(s1))
s1 = 'aba'
print (6, distinctSubseqII(s1))
s1 = 'aaa'
print (3, distinctSubseqII(s1))
test()