c++用链栈来实现算术表达式的计算

在我们的日常生活中，对于算术表达式我们更习惯使用操作符在操作数之间的中缀表达式，eg:2+3,但在用计算机实现算术表达式的运算时，考虑到运算效率以即各方面的因素时，将其转化为后缀(3 4 +)或者前缀表达式(+ 3 4)进行处理运算是一种更优的选择。

以下笔者采用后缀表达式来分析“用栈来实现算术表达式的计算”的具体实现过程。

一.实现思想
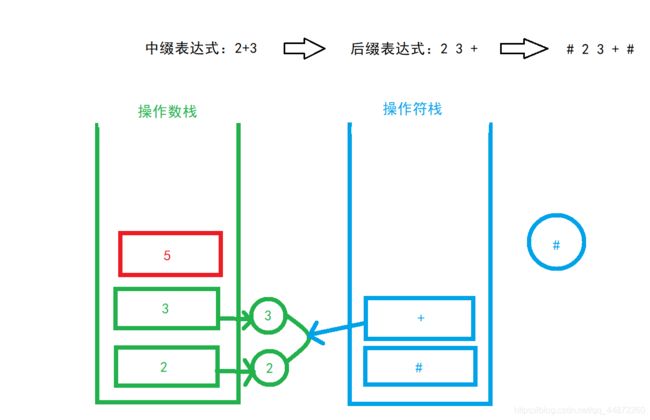
在进行算术运输时，我们必须要有操作数和操作符，操作数又分为左操作数和右操作数，而操作符也有相应的计算顺序，因此我们考虑用栈来实现这个过程。分别定义一个操作数栈和一个操作符栈来存储算术表达式，并对各操作符设定其优先级，下图为该函数的具体实现过程（在这里我们将运算式看作一个字符串，#一前一后用于判断式子的开始和结尾）。

二.注意事项
1.操作数出栈时，分为左操作数和右操作数，算得的结果要再次入栈
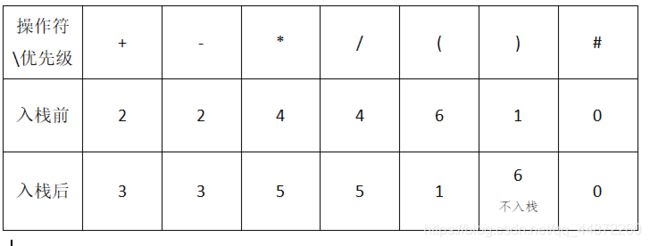
2.操作符栈内和栈外的优先级不同，而且右括号这个操作符不入栈
3.虑到操作数和操作符两个栈基本相同，对此我们使用模板类对其简化
4.关于find函数：如果查找成功则输出查找到的第一个位置，否则返回-1
5.关于各运算符的优先级。由于在算术运算中各运算符的运算顺序是不相同的，为了量化这样的顺序，我们在这里对其优先级用数字进行量化处理，并且分为栈内优先级和栈外优先级。每当读取一个运算符时，我们将其栈外优先级数值与操作符栈栈顶栈元素优先级进行比较，如果前者大于后者，则说明其紧迫程度高于栈顶元素，该运算符入栈。如果前者栈外优先级数值小于栈顶元素栈内优先级数值，则说明其紧迫程度小于栈顶元素，此时，操作符栈栈顶元素出栈，操作数栈依次弹出两个数作为左操作数和右操作数，运算结果再入操作数栈，然后再进行如上操作。整个过程中我们会发现右括号不会入栈。

三.实现代码
(linkedstack.h)

#ifndef LINKEDSTACK_H_INCLUDED
#define LINKEDSTACK_H_INCLUDED
//模板类定义一个结点类包含数据域和指针域
template<typename T>
class Node{
public:
  T data;   //数据成员
  Node<T>* next;

  Node(){next = 0 ;}  //无参构造函数初始化
  Node(const T &e){ data = e;next = 0;}  //有参构造函数初始化
};

//模板类定义一个栈
template <typename T>
class LinkStack{
public:
   LinkStack(){head = new Node<T>;}  //无参构造函数
   ~LinkStack();  //析构函数
   
   T& pop(); //出栈
   void push(const T& e );  //入栈
   T& getTop();  //获取栈顶元素
   bool ifEmpty(){return head->next == 0；} //判断是否为空栈
private:
   Node<T>* head;
};

#endif

函数实现代码块(linkedstack.cpp)

#include 
#include 
#include "linkedStack.h"
using  namespace std;
//析构函数
template<typename T>
LinkStack<T>::~LinkStack()
{
   Node<T>* p = head;
   while(head != 0)
   {
     p = p->next;
     delete(head);
     head = p;      
   }
}

//入栈
template<typename T>
void LinkStack<T>::push(const T& e)
{
    Node<T>* p = new Node<T>(e);  //初始化构造结点p
    p->next = head->next;
    head->next = p;
}

//出栈
template<typename T>
T& LinkStack<T>::pop()
{
    //如果栈为空栈，则程序结束
    if(ifEmpty())
    {
       exit(-1);
    }
    
    Node<T> * p = head->next; 
    static  T e;     //由于要返回栈顶元素，故将其定义为静态变量
    e = p->data;
    head->next = p->next;
    delete(p);
    
    return e;
}

//获取栈顶元素
template<typename T>
T& LinkStack<T>::getTop()
{ 
     //如果栈为空
     if(ifEmpty())
     { 
           exit(-1);
     }
     
     cout << head->next->data <<endl;
}

对表达式进行处理(experss.h)

#ifndef EXPRESSION_H_INCLUDED
#define EXPRESSION_H_INCLUDED
#include 
using namespace std;

const string OPR = "#(*/+-)";  //运算符列表
const int ISP_TABLE[7] = { 0,1,5,5,3,3,6};  //栈内优先级
const int ICP_TABLE[7] = { 0,6,4,4,2,2,1};  //栈外优先级

int isp(char op);// 返回运算符 op的栈内优先级
int icp(char op);// 返回运算符 op的栈外优先级

int calculate(int lh,int rh, char op);  //运算

//定义一个表达式类
class Expression
{
public:
    Expression(const string& s):exp(s) {} //有参构造函数初始化string
    void disp()
    {
        eval();
        cout << exp << "  = " << result << endl;  
    }
private:
    string exp;
    int result;
    void eval();
};

expression.cpp

#include 
#include "expression.h"
#include "linkedStack.cpp"

// 返回运算符栈内优先级
inline int isp(char opr)
{
    int idx = OPR.find(opr); //op在运算符表中的下标
    return ISP_TABLE[ idx ];  // 取对应的isp
}

// 返回操作符的栈外优先级
inline int icp(char opr)
{
    return ICP_TABLE[ OPR.find(opr) ];
}

//运算
int calculate(int lh,int rh, char op)
{
    switch(op)
    {
    case '+':
        return lh+rh;
    case '-':
        return lh-rh;
    case '*':
        return lh*rh;
    case '/':
        return lh/rh;
    }
}

void Expression::eval()
{
    //定义一个操作数栈和一个操作符栈，首先#操作符入栈，然后将表达式的结尾加上#字符便于判断
    LinkStack<int>  opnStk;     //操作数栈
    LinkStack<char> oprStk;     //操作符栈
    char ch;
    
    istringstream ist(exp+"#"); //可以实现对一行字符串以空格字符为分隔符进行读取操作
    oprStk.push('#');
    ist >> ch;
    while( !oprStk.ifEmpty() )
    {
        if(isdigit(ch))  //isdigit函数，主要用于检查其参数是否为十进制数字字符   
        {
            opnStk.push(ch-'0');
            ist >> ch;
        }
        else
        {
            if(icp(ch)> isp(oprStk.getTop()))//运算符的栈内优先级与栈外优先级的比较
            {
                oprStk.push(ch);
                ist >> ch;
            }
            else if(icp(ch)<isp(oprStk.getTop()))
            {
                int rh = opnStk.pop(); // left operand
                int lh = opnStk.pop(); // right operand
                int r = calculate(lh,rh,oprStk.pop());
                opnStk.push(r);
            }
            else if(icp(ch) == isp(oprStk.getTop()))
            {
                oprStk.pop();
                ist >> ch;
            }
        }
    }
    result = opnStk.pop();
}

主函数

#include "expression.h"
int main()
{
    Expression e1("2+3*2"), e2("(2+3)*2"),e3("(9-(5-(1+1))*3)"),e4("((6)+((5-1)))/(1+1)"),e5("1");
    
    e1.disp();
    e2.disp();
    e3.disp();
    e4.disp();
    e5.disp();
   
   return 0;
}