哈夫曼树及其引起的思考

一.什么是哈夫曼树?

哈夫曼树又称最优树，是一类带权路径长度最短的树。首先给出路径和路径长度的概念。从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称作路径长度。树的路径长度是从树根到每一个结点的路径长度之和。结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和，通常记作WPL。

对于哈夫曼树而言，其有一个非常显著的特点 ------- 没有度为1的结点.这类树又称严格的二叉树，对于这样的二叉树，根据其特点，如果其有n个叶子结点，则该哈夫曼树一共有2n-1个结点。

二.如何构建一颗哈夫曼树?

哈夫曼最早给出了了一个带有一般规律的算法，俗称哈夫曼算法。
（1）根据给定的n个权值{w1,w2,w3,…,wn}构成n颗二叉树的集合F={T1,T2,…,Tn}，其中每颗二叉树Ti中只有一个带权为wi的根结点，其左右子树均为空。
（2）在F中选取两颗根结点的权值最小的树作为左右子树构成一颗新的二叉树，且置新的二叉树的根结点的权值为其左右子树根结点的权值之和。
（3）在F中删除这两颗树，同时将新得到的二叉树加入F中。
（4）重复（2）和（3），直到F只含一棵树为止。这棵树便是哈夫曼树。

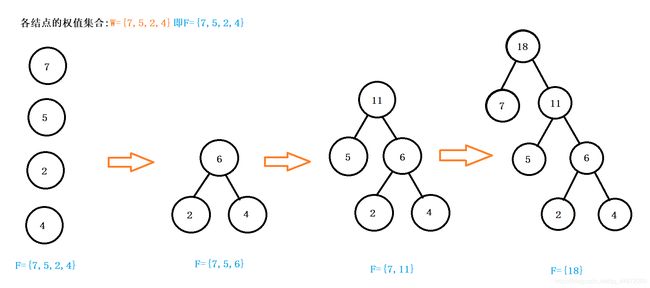
eg:给定如下权值集合{7,5,2,4},求解其哈夫曼树。

三.代码实现哈夫曼树及其引发的思考

分析：对于哈夫曼树的每一个结点，其必有左右子结点，根结点，和权值。为此我们创建一个该结点的结构体（在这里我另外增加了一个变量index，用于记录结点的下标）。

/*
创建一个结构体
*/
class HuffNode{
	int weight;  //结点的权值
	int lchild;  //结点的左孩子
	int rchild;  //结点的右孩子
	int parent;  //结点的双亲
	int index;   //结点的下标
}

1.为什么双亲和左右孩子的类型不是HuffNode?
由于后期笔者采用的是HuffNode数组来存放各个结点，所以我们只需要存储该该结点双亲和左右孩子在数组中的下标即可。这样的方式也大大节约的内存的开销。

2.为什么要设置index?
在整个构建哈夫曼树的过程中，由于们要找出所有树中权值最小的两个，这便要涉及到排序，而单单只对weight排序显然是不行的，我们必须将每一个HuffNode当做一个整体，然后根据HuffNode结点的weight值排序，是一个联动的效果，所以我们不仅要保存下标，而且在排序时，应该对其副本排序，再对应原始数据构建哈夫曼树。

3.java代码实现

import java.util.Scanner;

/*
 * 哈夫曼树
 * 测试数据:
 * 输入:
 * 8
 * 5 29 7 8 14 23 3 11
 * 输出: 
 * 100
 * */
public class Huffman {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();  //叶子结点的个数
		int[] w = new int[n];  //用于存储各个叶子结点的权值
		for(int i=0;i<n;i++) {
			w[i] = sc.nextInt();  //初始化前n个结点的weight值
		}		
		sc.close();
		
		//创建结点的结构体数组并完成初始化
		HuffNode[] date = new HuffNode[2*n-1];
		for(int i=0;i<2*n-1;i++) {			
			date[i] = new HuffNode(-1,-1,-1,-1,i);
		}
		for(int i=0;i<n;i++) {
			date[i].weight = w[i];
		}
		
		HuffNode[] copyDate = copy(date);  //数据的副本
		
		while(select(copyDate) != null) {
			HuffNode[] tempTwo = select(copyDate);
			date[n].weight = tempTwo[0].weight + tempTwo[1].weight;
			date[n].lchild = tempTwo[0].index;
			date[n].rchild = tempTwo[1].index;
			date[tempTwo[0].index].parent = date[n].index;
			date[tempTwo[1].index].parent = date[n].index;
			n++;
			copyDate = copy(date);
		}
		
		System.out.println(date[date.length-1].weight);
		
	}
	
	//选出双亲为负一的节点中，权值最小的两个
	public static HuffNode[] select(HuffNode[] date) {
		HuffNode[] sorteddate = QS(date,0,date.length-1);
		HuffNode[] twoLowest = new HuffNode[2];
		
		int flag = 0;
		for(int i=0;i<sorteddate.length;i++) {
			if(sorteddate[i].weight != -1 && sorteddate[i].parent == -1 && flag < 2) {
				twoLowest[flag] = sorteddate[i];
				flag++;
			}
		}
		
		if(flag == 1) {//flag等于1，说明哈夫曼树已经完成
			return null;
		}
		
		return twoLowest;
	}
	
	
	//快速排序,升序排列
	public static HuffNode[] QS(HuffNode[] date,int low,int high) {
		
		if(low>=high) {
			return date;
		}
		int l = low,h = high;
		
		int keyPoint = date[low].weight;
		while(l<h) {
			while(l<h && date[h].weight>=keyPoint) {
				h--;
			}
			HuffNode temph = date[h];
			date[h] = date[l];
			date[l] = temph;
			
			while(l<h && date[l].weight<=keyPoint) {
				l++;
			}
			HuffNode templ = date[l];
			date[l] = date[h];
			date[h] = templ;
		}
		
		if(low<high) {
			QS(date,low,l-1);
			QS(date,l+1,high);
		}
		
		return date;
	}
	
	//HuffNode数组复制函数
	public static HuffNode[] copy(HuffNode[] date) {
		HuffNode[] copy = new HuffNode[date.length];
		
		for(int i=0;i<date.length;i++) {
			copy[i] = new HuffNode(date[i].weight,date[i].lchild,date[i].rchild,date[i].parent,date[i].index);
		}
		
		return copy;
	}
}


//哈夫曼树的结点类
class HuffNode{
	int weight;   //该结点的权值
	int lchild;   //左子树
	int rchild;   //右子树
	int parent;   //双亲	
	int index;    //此变量的目的纯粹是为了后期方便哈夫曼树建立
	
	public HuffNode() {
		super();
	}

	public HuffNode(int weight, int lchild, int rchild, int parent, int index) {
		super();
		this.weight = weight;
		this.lchild = lchild;
		this.rchild = rchild;
		this.parent = parent;
		this.index = index;
	}
		
}

4.代码解析及思考
(1)数组拷贝之深浅拷贝

	//HuffNode数组复制函数
	public static HuffNode[] copy(HuffNode[] date) {
		HuffNode[] copy = new HuffNode[date.length];
		
		for(int i=0;i<date.length;i++) {
			copy[i] = new HuffNode(date[i].weight,date[i].lchild,date[i].rchild,date[i].parent,date[i].index);
		}
		
		return copy;
	}

在这里我自己实现了一个拷贝数组的算法。在编写整个代码的过程中，笔者最先使用的是HuffNode[] copyDate = date;。后来debug发现copyDate数组的值会和date数组的值同步变化。后来发现这样的该复制是一个浅拷贝。就是只会生成一个指针指向date数组，并不会为copyDate数组分配空间。解决方法有很多种，我们可以使用API中本身提供的深拷贝函数clone()等，也可以自行编写。

(2)快速排序的改进及其递归出口
这里的快速排序是对HoffNode数组进行排序并不是单纯的数字排序，涉及到“捆绑联动”的问题。其次在快速排序前，一定先要验证是否到了递归出口，否者会形成空指针异常。

(3)如何确定哈夫曼树是否构建完成?
当完成哈夫曼树后，我们在对数组进行遍历时，必然只会找到一个节点的parent值为-1,也就是说此时flag的值为1，返回null值，这便是判断哈夫曼树是否完成的标志。