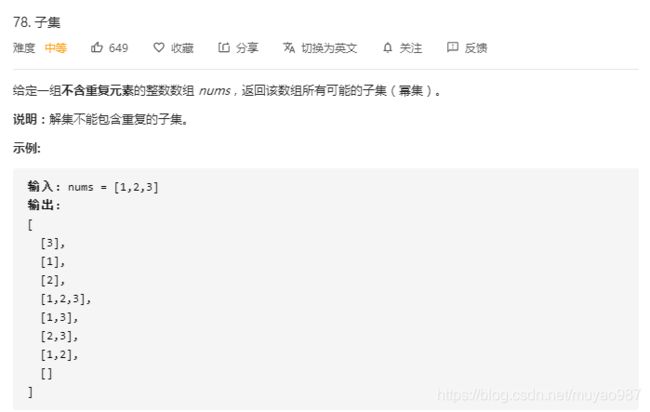
【Python刷题Leetcode】递归/回溯/分治（求子集、组合求和、括号生成、逆序数）

非递归解法：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        output = [[]]
        
        for num in nums:
            output += [curr + [num] for curr in output]
            print(output)
        
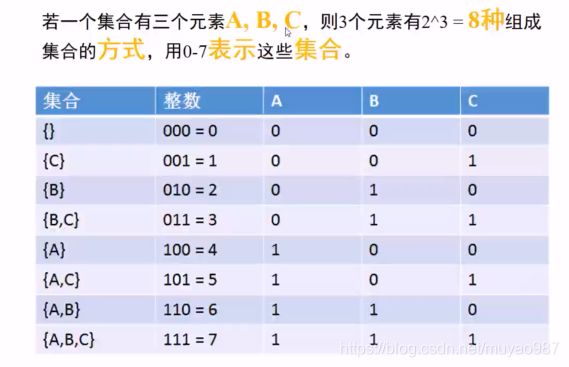
        return output

位运算法：

这个题nums可能包含重复元素。

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        res = [[]]

        for n in nums:
            tmp = [[n]+each for each in res]
            for each in tmp:
                if sorted(each) not in res:
                    res.append(sorted(each))
        return res

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates = sorted(candidates) # 排序
        res = [] # 初始化结果

        def func(idx, cur_sum, cur_res):
            for i in range(idx, len(candidates)):
                # 加上当前值超了 直接剪枝
                if cur_sum+candidates[i] > target:
                    break
                elif cur_sum+candidates[i] == target:
                    res.append(cur_res + [candidates[i]])
                    break
                else:
                    func(i, cur_sum+candidates[i], cur_res+[candidates[i]])
        
        func(0,0,[])
        return res

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates = sorted(candidates) # 排序
        res = [] # 初始化结果

        def func(idx, cur_sum, cur_res):
            for i in range(idx, len(candidates)):
                # 加上当前值超了 直接剪枝
                if cur_sum+candidates[i] > target:
                    break
                elif cur_sum+candidates[i] == target:
                    tmp = cur_res + [candidates[i]]
                    # 这里判断是否已经加到了res中
                    if tmp not in res:
                        res.append(tmp)
                    break
                else:
                    # 这里和39题相比 改成i+1 因为每个数字只能用一次
                    func(i+1, cur_sum+candidates[i], cur_res+[candidates[i]])
        
        func(0,0,[])
        return res

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        result = []

        # 递归生成所有情况的组合
        def generate(item, can_left_num, can_right_num):
            # item：当前已生成的字符串
            # can_left_num：当前还能放多少(
            # can_right_num：当前还能放多少)

            # 限制条件1: 左括号或右括号数量要分别小于n
            # 限制条件2：先放左括号 再放右括号(右括号始终<=左括号)

            if len(item)==2*n: # item扩到了满长(2n)
                result.append(item)
                return
            
            # 分别扩展左右括号
            # 【限制条件1】当还能放的左括号数量(最多为n)大于0时
            if can_left_num>0:
                generate(item+'(', can_left_num-1, can_right_num)
            
            # 【限制条件2】当还能放的右括号数量大于左括号时(保证左括号在前)
            if can_right_num > can_left_num:
                generate(item+')', can_left_num, can_right_num-1)
        
        # 调用递归函数生成所有情况(2^2n种情况：每个位置可)可( ,总长度是2n)
        generate('', can_left_num=n, can_right_num=n)
        return result

 

---

归并排序，两个把idx和num绑定

左右都有序时，对于left中i所指的num，right中j左边的那些肯定都比num小

class Solution:
    def countSmaller(self, nums: List[int]) -> List[int]:
        arr = []
        res = [0] * len(nums)
        # idx和nums绑定
        for idx, num in enumerate(nums):
            arr.append((idx, num))
        # indx = [0,1,2,3]
        # nums = [5,2,6,1]
        # arr  = [(0,5), (1,2), (2,6), (3,1)]

        # 归并排序，在合并的时候，可以判断出右边比它小的个数
        def merge_sort(arr):
            if len(arr) <= 1:
                return arr
            mid = len(arr) // 2
            left = merge_sort(arr[:mid])
            right = merge_sort(arr[mid:])
            return merge(left, right)

        # 主要是merge函数 记录当前tmp 左右都是排好序的
        def merge(left, right):
            tmp = []
            i = 0
            j = 0
            while i < len(left) or j < len(right):
                # left中的当前元素小于等于right中的当前元素
                if j == len(right) or i < len(left) and left[i][1] <= right[j][1]:
                    tmp.append(left[i])
                    res[left[i][0]] += j
                    i += 1
                else:
                    tmp.append(right[j])
                    j += 1
            return tmp

        merge_sort(arr)
        return res