数据结构 --- 线性表 顺序储存 链式储存

线性表是平时一直会用到的数据结构，像python里面的list这种高级数据结构，其实也是对这种底层结构的封装。

这篇文章写了整整4天........

线性表的储存结构主要分两大类，一类一类来看。

在这之前，先用伪代码来形容一下线性表拥有的基本功能

1 ：顺序储存结构

听名字就知道，这是按照顺序来排的，简单来说，就是在用顺序储存结构来建立线性表的时候，他是在内存里面先申请一块空地

然后，所有的相同类型的数据元素按照顺序，放进去，并且，在内存中的存放，也是连续的！

也就是打个比方a,b,c三个元素的内存地址，如果按照顺序储存结构的话就会是0x00001 ---> 0x00002 ---> 0x00003

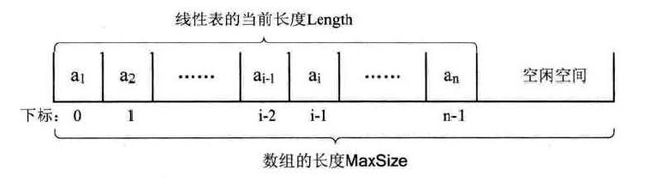
另外，顺序储存的时候，由于是先申请内存空间，再放入线性表，所以，正常来说，数组长度(也就是申请的空间大小)是大于等于线性表长度的

其次，数组内元素的下标，是要比第i个元素的i少一位的，如下图.

概括一下，线性表的储存结构可以用以下代码来抽象表示

#define MAXSIZE 20 /* 存储空间初始分配量 */

typedef struct
{
	ElemType data[MAXSIZE];        /* 数组，存储数据元素 */
	int length;                                /* 线性表当前长度 */
}SqList;

每个数据元素，其实在内存中都有他的固定地址的

然后由于顺序线性表的都是连续固定的，所以根据每种元素的数据类型的不同，你可以看出后面元素的不同内存地址

假设我们存放的是整数int，他每个元素要占用c个空间，那么我们用LOC(a)来表示a这个元素的内存地址的话

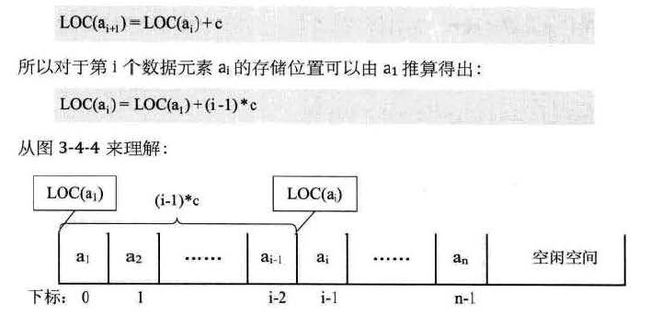
那么LOC(ai+1)=LOC(ai)+C

那么LOC(ai)可以根据a1的LOC来推算出他的内存地址LOC(ai)=LOC(a1)+(i-1)*c

所以，由于内存地址都是连续的，所以你完全可以通过第一个元素就知道其中第i个元素的值，所以，读取或存放的时间复杂度为O(1)

1 顺序储存线性表的元素获取

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

typedef int Status;          /* Status是函数的类型,其值是函数结果状态代码，如OK等 */

/* 初始条件: 顺序线性表L已经存在，1≤i≤ListLength(L) */

/* 操作结果: 用e返回L 中第i个数据元素的值 */

Status GetElem(SqList L,int i,ElemType *e)   /* 这里等于是定义GetElem返回时整型 ，这句函数其实等于int GetElem  */
{
    if(L.length==0 || i<1 || i>L.length)
            return ERROR;
    *e=L.data[i-1];

    return OK;
}

如果数组长度为0 或 i小于1 或 i 大于数组长度最大位的后一位，直接返回ERROR

否则，代表能读到这个数，则给 *e 赋值，值为数组数据的第i-1下标位的数值，并返回OK

2 顺序储存线性表的元素插入

这个原理和插队是一样的，比如一共10个人的队伍，你认识第4个人，你让他给你插下队，那你认识的人就变成第5个了，你变成了第4个，队列长度要加1

/* 初始条件：顺序线性表L已存在,1≤i≤ListLength(L)， */
/* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
Status ListInsert(SqList *L,int i,ElemType e)
{ 
	int k;
	if (L->length==MAXSIZE)  /* 顺序线性表已经满 */
		return ERROR;
	if (i<1 || i>L->length+1)/* 当i比第一位置小或者比最后一位置后一位置还要大时 */
		return ERROR;

	if (i<=L->length)        /* 若插入数据位置不在表尾 */
	{
		for(k=L->length-1;k>=i-1;k--)  /* 将要插入位置之后的数据元素向后移动一位,k>=i-1等于是说明，当新元素的下标k，越过i-1时 */
			L->data[k+1]=L->data[k]; /*每次历遍都把当前下标位k的元素向后移动一位*/
	}
	L->data[i-1]=e;          /* 将新元素插入 */
	L->length++;

	return OK;
}

这里注意，温习一下，指针访问结构体成员的方法是L->length，如果是结构体变量访问成员的话，是 xxx.length

3 顺序储存线性表的元素删除

/* 初始条件：顺序线性表L已存在，1≤i≤ListLength(L) */
/* 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 */
Status ListDelete(SqList *L,int i,ElemType *e) 
{ 
    int k;
    if (L->length==0)               /* 线性表为空 */
		return ERROR;
    if (i<1 || i>L->length)         /* 删除位置不正确 */
        return ERROR;
    *e=L->data[i-1];                /* 用第i个元素给e赋值 */
    if (ilength)                /* 如果删除不是最后位置 */
    {
        for(k=i;klength;k++)/* 将删除位置后继元素前移 */  
			L->data[k-1]=L->data[k];  /* 通过元素下标前移元素 */
    }
    L->length--;
    return OK;
}

通过插入元素和删除元素，我们可以看到，需要对元素进行操作的话，最坏情况下，是每个元素都要移动一下。

所以这时候的时间复杂度是O(n)

至此可以看出顺序储存结构线性表的优缺点了

2.链式储存结构线性表

链式储存结构和顺序结构正好相反，他的元素存放，不是排排坐吃果果般连续的，而是分散的，说不定是内存地址0x00001------>0x00013------>0x00022

但是，前一个元素，会知道后一个元素的内存地址，他是如何知道的呢

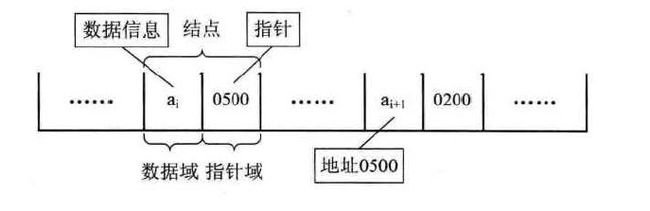
这是因为，链式储存结构的元素，不光光有数据值，他还有指针域，指向后一个元素

这样，我们把数据域+指针域称为结点Node

每个结点只包含一个指针域的，叫做单链表

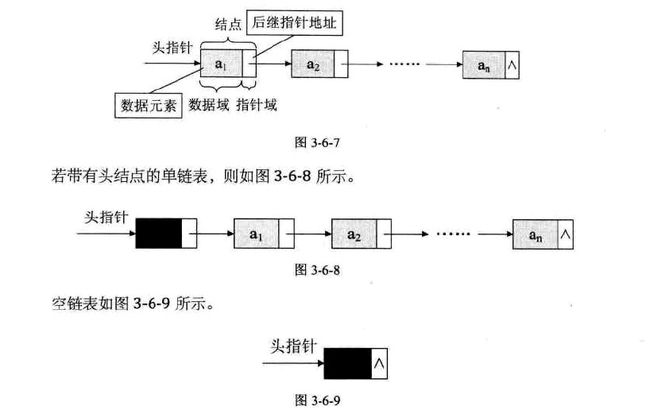
作为单链表来说，总得有一个指向第一个元素结点的东东，这里，叫做头指针，单链表里面必须有的东西。

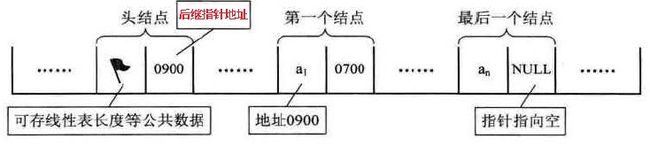
头指针只有指针域，他指向的是第一个结点的地址.

而相对的，最后一个元素结点的指针域，指向的结果是NULL

另外，有时我们还会在头指针和第一个元素结点的中间，添加一个头结点，这个结点的数据域可以不存放东西，也可以存放如数组长度啊这些的信息，他的指针域指向第一个元素结点。

然后来看下头指针和头结点的区别

这样，总结一下储存示意图

其实对于链表来说，他都是由一个一个结点组成的

所以，我们可以用结构指针来表示链表

typedef struct Node
{
    ElemType data;            /* 数据域 */
    struct Node *next;        /* 指针域 */
}Node;                        /* 取个别名Node，方便操作 */
typedef struct Node *LinkList; /* 定义LinkList，指向结构体Node的指针 */

假设我们有个指针p，指向链表的第i个结点，那么p->data就表示数据域，p->next就表示指针域

p->next指向的是下一个结点，如果要指向下一个结点的数据域，则是表示成p->next->data

1 单链表的读取

对于单链表来说，你要获取一个元素，你必须从头开始历遍

/* 初始条件：顺序线性表L已存在，1≤i≤ListLength(L) */
/* 操作结果：用e返回L中第i个数据元素的值 */
Status GetElem(LinkList L,int i,ElemType *e)
{
	int j;
	LinkList p;		/* 声明一指针p */
	p = L->next;		/* 让p指向链表L的第一个结点 */
	j = 1;		/*  j为计数器 */
	while (p && jnext;  /* 让p指向下一个结点 */
		++j;
	}
	if ( !p || j>i ) 
		return ERROR;  /*  第i个元素不存在 */
	*e = p->data;   /*  取第i个元素的数据 */
	return OK;
}

这里需要注意一下，上一个章节里面讲顺序储存结构线性表的时候，SqList是一个结构体别名, 他定义生成的对象是实例变量

而这个章节的LinkList，是一个指向结构体Node的指针！他定义生成的对象是一个指针！

还有p=L->next不是将L的下一个结点赋值给p，而是将p指向L的下一个结点，p还是指针类型！

上面这个获取元素的代码，他在 j 未达到 i 的过程中，循环将p结点向后移动，他将在  j=i 的时候, 将当前p的data，也就是储存的数值，赋值给 *e

最后return Ok

而通过链表的结构我们可以知道，只有上一个结点才知道下一个结点在哪里，所以，当你需要知道一个结点的值的时候，只能从开头一个一个历遍

所以，他的时间复杂度是O(n)

2 单链表的插入

事物总有两面性，链表的读取的时间复杂度是O(n) ，那肯定也有优点，来看看单链表的插入

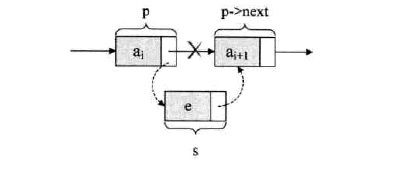
简单来说，链表的插入就是，把新结点的后继指针指向原来这个位置的结点，再把前一个结点的后继指针指向新结点

先后次序可以概括为  s->next = p->next ，然后 p->next = s

这里得记住，千万不能颠倒次序，如果你先将p->next=s进行了赋值，那后面s->next就等于他s自己了，等于断链了。

    

/* 初始条件：顺序线性表L已存在,1≤i≤ListLength(L)， */
/* 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1 */
Status ListInsert(LinkList *L,int i,ElemType e)
{ 
	int j;
	LinkList p,s;
	p = *L;                /* p还是指针，指向第一个结点 */
	j = 1;
	while (p && j < i)     /* 寻找第i个结点 */
	{
		p = p->next;   /* 这句很重要，他并不是说p是p的下一个结点，而是说，p从指向当前结点，变成指向下一结点 */
		++j;
	} 
	if (!p || j > i) 
		return ERROR;   /* 第i个元素不存在 */
	s = (LinkList)malloc(sizeof(Node));  /*  生成新结点(C语言标准函数) */
	s->data = e;  
	s->next = p->next;      /* 将p的后继结点赋值给s的后继  */
	p->next = s;          /* 将s赋值给p的后继 */
	return OK;
}

这段代码再附加解释一下

LinkList p,s是定义了2个结构体指针p和s

并通过p=*L的语句，让p指第一个结点, 具体意思是，传入的是头指针本身的内存地址，然后再用 * 解引用，解出来的就是头指针的内存地址

注意一下，这里的LinkList *L ，涉及到了C语言里，函数参数传递的规则.

*L表示地址传递，虽然在C里面没有真正意义上的地址传递。

所以这个过程应该是，传入L实参的地址，即传入形参*L的值为  &L (是指针L的本身内存地址)，也就是要操作指针L的地址的话，需要用一个二级指针来做 * 操作

另外，我理解，这个L其实是一个头指针，他的指针域是指向第一个结点的

这部分会比较难理解，自己画了个图

从上面的结构图可以看出，p=*L 就等于指针L的地址，在第一轮历遍的时候，头指针和p是重合的，但是在后面的历遍中，p会不断地向后移动

为什么不用值传递！因为，值传递不改变实际参数，而地址传递是在内存地址上进行操作的，所以改变实际参数的！

而这里插入元素，是需要改变原来L链表的结构的!!

当开始循环的第一遍时，p 就指向第一个结点，并且在p && jnext，也就是p指针的指向，从当前位置后移一位

3 单链表的元素删除

删除和插入没啥大的结构上区别，也即是把前驱指针和后继指针进行调整，注意顺序

/* 初始条件：顺序线性表L已存在，1≤i≤ListLength(L) */
/* 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1 */
Status ListDelete(LinkList *L,int i,ElemType *e) 
{ 
	int j;
	LinkList p,q;
	p = *L;
	j = 1;
	while (p->next && j < i)	/* 遍历寻找第i个元素 */
	{
        p = p->next;
        ++j;
	}
	if (!(p->next) || j > i) 
	    return ERROR;           /* 第i个元素不存在 */
	q = p->next;
	p->next = q->next;			/* 将q的后继赋值给p的后继 */
	*e = q->data;               /* 将q结点中的数据给e */
	free(q);                    /* 让系统回收此结点，释放内存 */
	return OK;
}

4 单链表的整表创建

链表的创建实际上是一个动态的过程，因为每次多加一个元素，他的内存空间才会扩充一次，即用即扩展，所以他需要用到malloc

另外新建链表也可以有2种方法，头插法和尾插法

先来看头插法

/*  随机产生n个元素的值，建立带表头结点的单链线性表L（头插法） */
void CreateListHead(LinkList *L, int n) 
{
	LinkList p;
	int i;
	srand(time(0));                         /* 初始化随机数种子 */
	*L = (LinkList)malloc(sizeof(Node));
	(*L)->next = NULL;                      /*  先建立一个带头结点的单链表 */
	for (i=0; idata = rand()%100+1;             /*  随机生成100以内的数字 */
		p->next = (*L)->next;    
		(*L)->next = p;						/*  插入到表头 */
	}
}

没啥好多说的，有一句需要着重强调

*L = (LinkList)malloc(sizeof(Node))

这句的意思是什么？(LinkList)malloc(sizeof(Node)) 返回的是一个指针变量！！！是指向一个结点(也就是头结点)的指针！！！

而这个等式，让*L这个指针，被引向了指向头结点的指针，在此刻等同于头结点的指针

为什么说是创建了一个头结点，是因为(*L)->next = NULL

接着是尾插法，这个属于一般比较正常的思路，从尾部插入

/*  随机产生n个元素的值，建立带表头结点的单链线性表L（尾插法） */
void CreateListTail(LinkList *L, int n) 
{
	LinkList p,r;
	int i;
	srand(time(0));                      /* 初始化随机数种子 */
	*L = (LinkList)malloc(sizeof(Node)); /* L为整个线性表 */
	r=*L;                                /* r为指向尾部的结点 */
	for (i=0; idata = rand()%100+1;           /*  随机生成100以内的数字 */
		r->next=p;                        /* 将表尾终端结点的指针指向新结点 */
		r = p;                            /* 将当前的新结点定义为表尾终端结点 */
	}
	r->next = NULL;                       /* 表示当前链表结束 */
}

这里又有一个比较重要的语句  r=*L

这里 *L 是指向头结点的指针，但是L是代表整个线性表，他会随着n的增大而增大

r是指向结点的指针，但是他会在每次历遍，指向不同的结点

为什么要这样区分呢？因为链表的长度的计算，是按照从*L这个头结点开始，经过n次历遍，直到最后一个结点的next为NULL的时候才停止。

也就是说,  *L必须停留在起始位置

而 r 在程序刚开始的时候和*L是重合的。只是在后面的历遍过程中，逐渐分开了。

r 在历遍过程中，始终为指向最后一个节点的指针。

两个语句需要补充理解：

r->next = p    将r 和新的结点p进行连接

r = p ，将当前指向 r 的指针 引向 p ,也就是当前最后一个结点，等于是刷新了 r

这里补充一下计算链表长度的函数，就可以看到，为什么*L要停留在头部

/* 初始条件：顺序线性表L已存在。操作结果：返回L中数据元素个数 */
int ListLength(LinkList L)
{
    int i=0;
    LinkList p=L->next; /* p指向第一个结点 */
    while(p)                        
    {
        i++;
        p=p->next;
    }
    return i;
}

计算过程从L开始历遍，每次历遍计数器加1 ，最后返回的是计数器数字

5 单链表的整表删除

他关键也是用到指针的移动和free函数

/* 初始条件：顺序线性表L已存在。操作结果：将L重置为空表 */
Status ClearList(LinkList *L)
{ 
	LinkList p,q;
	p=(*L)->next;           /*  p指向第一个结点 */
	while(p)                /*  没到表尾 */
	{
		q=p->next;
		free(p);
		p=q;
	}
	(*L)->next=NULL;        /* 头结点指针域为空 */
	return OK;
}

从前往后依次free掉结点，组后把头结点的next设为NULL，即置空！

这样，两种储存结构的线性表，就基本是这样，下一篇再写点循环链表和双向链表.