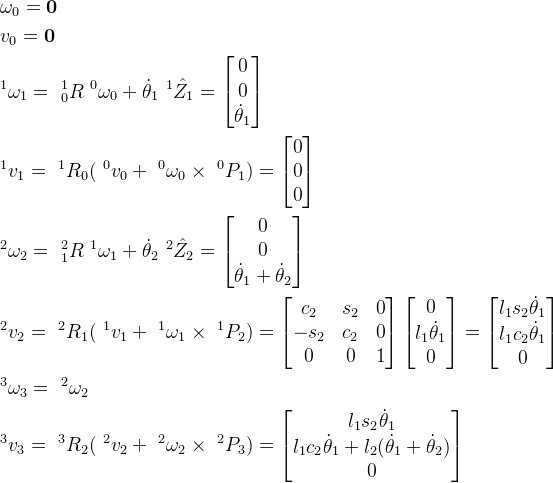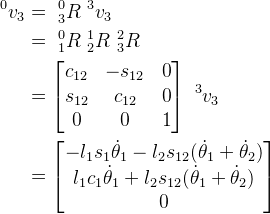【数学问题2】动力学基础
在先前的文章中,我们已经讨论过了四足机器人的腿部运动学建模,但是仅有运动学部分是不够的的,因为机器人时刻出于运动当中,是一个时变系统,在此运动中,机器人的速度,加速度也可能会时间变化。而涉及到加速度,就离不开力,涉及到力的分析,就离不开动力学。
现在,我们先将问题简化,假定机身是固定在空间中的某一点上,来分析腿部模型的动力学模型
一、速度和静力
要研究动力学,我们首先从刚体运动开始
1.1 时变位姿符号表示
下面下来讨论一些基本知识:向量微分,角速度的表示及符号
位置向量的微分
当物体的质量可以集中于一点时,我们可以忽略物体本身的旋转,只考虑其线速度。
定义参考系{B}中一点Q,其位置表示为 B P Q ^BP_Q BPQ,其速度为 B V Q ^BV_Q BVQ
因此有以下关系:
B V Q = d B P Q d t = l i m Δ t → 0 B P Q ( t + Δ t ) − B P Q ( t ) Δ t ^BV_Q = \frac{d^BP_Q}{dt} = \underset{\Delta t\rightarrow 0}{lim}\frac{^BP_Q(t+\Delta t)- ^BP_Q(t)}{\Delta t} BVQ=dtdBPQ=Δt→0limΔtBPQ(t+Δt)−BPQ(t)
上式描述了,Q点位置的时间微分,即Q点的速度(B参考系下)。
参考系是非常重要的,这点不能忽略,举个例子,Q点在坐标系B下观察时,其速度不随时间变化,即速度为0,而参考系{B}本身有可能是运动的,因此,点Q在其他参考系下观察时,其速度不一定为0
与位置变换类似,速度也是可以在不同坐标系下进行变化的:
A ( B V Q ) = A ( d B P Q d t ) = B A R B V Q ^A(^BV_Q) = ^A(\frac{d^BP_Q}{dt}) = _{B}^{A}\textrm{R}^BV_Q A(BVQ)=A(dtdBPQ)=BARBVQ
多数情况下会讨论某一个坐标原点相对于世界参考系的速度,此时不去深究其相对于其他任意坐标系的的速度,这种情况下会写作:
v c = U V C O R G v_c = ^UV_{CORG} vc=UVCORG
角速度向量
当物体不能看做是一个质点时,我们就得考虑其本身的旋转,通常用角速度来描述。用 Ω \Omega Ω表示。

上图中 A Ω B ^A\Omega_B AΩB描述了坐标系{B}相对于于坐标系{A}的旋转
现在讨论一种情况,假设从坐标系{B}观察点Q,其位置不随时间变化,而{B}相对于于坐标系{A}的旋转,计算Q点在{A}下的速度(具体推导过程略):
A V Q = A Ω B × A P Q ^AV_Q = \ ^A\Omega_B \ \times \ ^AP_Q AVQ= AΩB × APQ
其中:
A P Q = B A R B P Q ^AP_Q = \ ^A_B R \ ^BP_Q APQ= BAR BPQ
一般情况下,点Q是相对于{B}变化的,因此需要加上线速度分量:
A V Q = A R B B V Q + A Ω B × B A R B P Q ^AV_Q = \ ^AR_B \ ^BV_Q + ^A \Omega_B\ \times \ ^A_BR \ ^BP_Q AVQ= ARB BVQ+AΩB × BAR BPQ
加上原点的线速度,将上式推广到坐标原点不重合的情况:
A V Q = A V B O R G + B A R B V Q + A Ω B × B A R B P Q ^AV_Q =\ ^AV_{BORG} + \ ^A_BR \ ^BV_Q \ + \ ^A \Omega_B \ \times \ ^A_BR \ ^BP_Q AVQ= AVBORG+ BAR BVQ + AΩB × BAR BPQ
二、机器人连杆运动
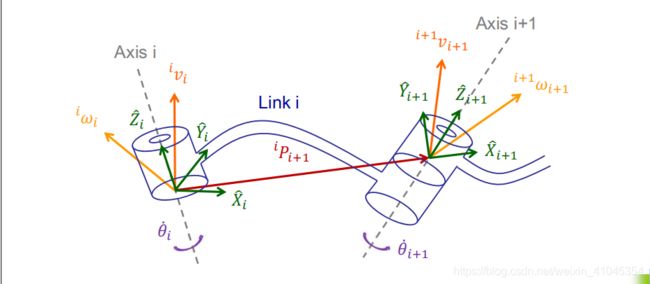
规定 ω i \omega_i ωi为连杆坐标系 { i } \{i\} {i}的角速度, v i v_i vi为连杆坐标系原点的线速度。由于操作臂是链式结构,每一个连杆的运动都与它相邻杆有关
旋转关节
根据DH模型,我们计算其角速度值:
i ω i + 1 = i ω i + i + 1 i R θ ˙ i + 1 i + 1 Z ^ i + 1 ^i \omega_{i+1} = \ ^i \omega_i + ^i_{i+1}R \dot \theta_{i+1} \ ^{i+1}\hat Z _{i+1} iωi+1= iωi+i+1iRθ˙i+1 i+1Z^i+1
其中:
θ i + 1 i + 1 Z ^ i + 1 = i + 1 [ 0 0 θ ˙ i + 1 ] \theta_{i+1} \ ^{i+1}\hat Z _{i+1} =\ ^{i+1} \begin{bmatrix} 0 \\ 0\\\dot \theta_{i+1} \end{bmatrix} θi+1 i+1Z^i+1= i+1⎣⎡00θ˙i+1⎦⎤
需要注意,DH模型中我们定义旋转轴为Z轴,因此才会有 θ i + 1 i + 1 Z ^ i + 1 \theta_{i+1} \ ^{i+1}\hat Z _{i+1} θi+1 i+1Z^i+1
由于连杆 i + 1 i+1 i+1的角速度是由关节运动产生,因此第 i + 1 i+1 i+1个连杆相对于第 i i i连杆的角速度,等于连杆 i i i本身的角速度加上连杆 i + 1 i+1 i+1的关节角速度
两边同时乘以 i i + 1 R ^{i+1}_{i}R ii+1R,对观测坐标系进行变换,我们得到:
i + 1 ω i + 1 = i i + 1 R i ω i + θ ˙ i + 1 i + 1 Z ^ i + 1 ^{i+1} \omega_{i+1} = ^{i+1}_{i}R \ ^i \omega_i + \dot \theta_{i+1} \ ^{i+1}\hat Z _{i+1} i+1ωi+1=ii+1R iωi+θ˙i+1 i+1Z^i+1
对于线速度:
i v i + 1 = i v i + i ω i × i P i + 1 ^iv_{i+1} = \ ^iv_i + \ ^i\omega_i \times \ ^iP_{i+1} ivi+1= ivi+ iωi× iPi+1
两边同时乘以 i i + 1 R ^{i+1}_{i}R ii+1R,得到:
i + 1 v i + 1 = i i + 1 R ( i v i + i ω i × i P i + 1 ) ^{i+1}v_{i+1} =^{i+1}_{i}R ( \ ^iv_i + \ ^i\omega_i \times \ ^iP_{i+1}) i+1vi+1=ii+1R( ivi+ iωi× iPi+1)
三、应用

以上述两自由度机械臂为例。我们根据各关节角速度,求解 V 3 , V_3, V3,其变换矩阵依次为:
1 0 T = [ c 1 − s 1 0 0 s 1 c 1 0 0 0 0 1 0 0 0 0 1 ] ^0_1T = \begin{bmatrix} c_1 & -s_1 & 0 & 0\\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} 10T=⎣⎢⎢⎡c1s100−s1c10000100001⎦⎥⎥⎤
2 1 T = [ c 1 − s 1 0 l 1 s 1 c 1 0 0 0 0 1 0 0 0 0 1 ] ^1_2T = \begin{bmatrix} c_1 & -s_1 & 0 & l_1\\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} 21T=⎣⎢⎢⎡c1s100−s1c1000010l1001⎦⎥⎥⎤
3 2 T = [ 1 0 0 l 2 0 1 0 0 0 0 1 0 0 0 0 1 ] ^2_3T = \begin{bmatrix} 1 & 0 & 0 & l_2\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} 32T=⎣⎢⎢⎡100001000010l2001⎦⎥⎥⎤
我们可以依次计算其线速度,角速度,由于坐标系 0 {0} 0是固定在地面上的,因此: