兔兔 的 总结 —— 树状数组

树状数组

---

---

一. 问题的提出

有一个一维数组，长度为 $n$ 。
你可以对这个数组进行两种操作：

1. 修改： 对 $1$ ~ $n$ 之间的一个元素 $num[k]$ 增加 $v$。
2. 求和： 求 $i$ 到 $j$ 的和。

常见的做法就是： $循环累加$ 和 $前缀和$

1. 循环累加

代码如下：

// 修改
num[k] += v;

// 求和
for (int k = i; k <= j; k++) cnt += num[i];
printf("%d\n", cnt);

2. 前缀和

代码如下：

// 修改
num[k] += v;
for (int i = k; i <= n; i++) pre[i] = pre[i - 1] + num[i];

// 求和
printf("%d\n", pre[j] - pre[i - 1]);

但是上面两种方法的时间复杂度都很大，这里就需要用到树状数组了。

---

二. 概念

树状数组 —— Binary Indexed Tree(B.I.T) 也称作 Fenwick Tree ： 它是一个 $查询$ 和 $修改$ 的时间复杂度都为 $lo{g}_{2}n$ 的数据结构。它主要用于查询两点之间的所有元素之和。

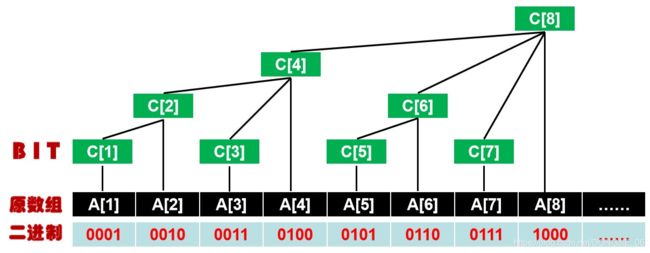
图片的大概意思：
$A$ ：输入的数组
$C$ ：树状数组

$C_1=A_1$
$C_2=C_1+A_1=A_1+A_2$
$C_3=A_3$
$C_4=C_2+C_3+A_4=A_1+A_2+A_3+A_4$
$C_5=A_5$
$C_6=C_5+A_6=A_5+A_6$
$C_7=A_7$
$C_8=C_4+C_6+C_7+A_8=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8$

这就是 树状数组 (它长得像树一样 ，所以称为 树状数组 )。

---

下面我们将学习

1. " 如何求已知数组下标的树状数组 $Bit[i]$ 的$子叶个数(lowbit)$ (也就是上面的 $C$ 数组所含的 $A$ 数组的个数，例如：$C_1$ 的子叶个数为 $1$ ，$C_3$ 的子叶个数为 $1$ ，$C_4$ 的子叶个数为 $4$ ······) " 。
2. " 如何对树状数组进行$修改$ " 。
3. " 如何用树状数组求$前缀和$ " 。
   ······

1. $lowbit$

(1). 什么是 $lowbit$ ?

$lowbit(i)$ 是将 $i$ 转化成二进制数之后，只保留最低位的 $1$ 及其后面的 $0$ ，舍去前面的所有数字，然后再转成十进制数，这个数也是树状数组中 $i$ 号位的子叶个数。
例如： $lowbit(22)$ ，它的意思是将 $22$ 转化成二进制数之后，得到 $10110$ ，保留最后一个 $1$ 及其它后面的 $0$，并舍去前面的所有数字，得到 $10$，转化为十进制数为2，即 $lowbit(22)=2$，所以 $C[22]$ 的子叶个数为 $2$ 。

我们自己在草稿纸上可以计算 $lowbit(i)$ ，但是在 $C++$ 中怎么实现呢？
下面，我会教给大家几种常见的方法：

• 我们先来熟悉一下位运算中的按位与 & ：
  $0$ & $0=0$
  $0$ & $1=0$
  $1$ & $0=0$
  $1$ & $1=1$

• 求 $lowbit$ 方法一：
  原数为 $x$ (十进制)，先将原数转化成二进制，之后将它的最后一个 $1$ 替换成 $0$ 得到 $x^{\prime }$ ，然后再用 $x$ 减去 $x^{\prime }$ (十进制相减)，答案就是 $lowbit(x)$ 的结果。参考代码如下：

int lowbit(int x)
{
	return x - (x & (x - 1));
}

有些读者可能看不太懂。
我给大家解释一下：$x$ 的二进制可以看做 $A1B$ ( $A$ 是最后一个 $1$ 之前的部分， $B$ 是最后一个 $1$ 之后的 $0$ )
$x-1$ 的二进制可以看做 $A0C$ ( $C$ 是和 $B$ 一样长的 $1$ )
$x$ & $(x-1)$ 的二进制就是 $A1B$ & $A0C$ = $A0B$
$x-(x$ & $(x-1))$ 的二进制就是 $A1B–A0B=0\dots 010\dots 0$
就得到我们所求的 $lowbit(x)$了。

• 求 $lowbit$ 方法二：
  原数为 $x$ (十进制)，先将原数转化成二进制之后，在和原数的相反数 $-x$ 的二进制进行按位与，答案就是 $lowbit(x)$的结果。参考代码如下：

int lowbit(int x)
{
	return x & (-x);
}

例如：$lowbit(22)$：
$22$ 的二进制原码 $011010$ ，正数的补码等于它的原码 $011010$
$-22$ 的二进制原码 $111010$ ，负数的补码等于它的原码取反加 $1$ ，为
$100101+1=100110$ (二进制)。
$011010$ & $100110=000010$ 正数转换成原码后依然是 $000010$
所以 $lowbit(22)=2$
至于为什么是这样的，就留给读者自己思考了。

2. $update$

(1). 什么是 $update$ ?

$update$ 就是用来更新树状数组的一个函数。

(2). 怎么用 $lowbit$ 更新 $update$ ?

在上面的 $lowbit$ 中，我们可以发现一个规律 (其实博主也不知道怎么证明，如果有知道的小伙伴，可以在博客下方评论哟~)：对于任意一个下标为 $i$ 的 $A$ 数组 $A[i]$ ，包含它的树状数组 $C[]$ 的下标就是 $i$ 每次加上当前阶段的 $lowbit(i)$。
例如：上面的 $A_3$，$C_3$ 就含有 $A_3$， 因为$lowbit(3)$ 是 $1$ ，所以 $3+1=4$ ；接着是 $C_4$，所以 $C_4$ 也含有 $A_3$， $lowbit(4)$ 是 $4$ ，所以 $4+4=8$ ；接着就是 $C_8$， 所以 $C_8$ 也含有 $A_3$ ，$lowbit(8)$ 是 $8$ ，所以 $8+8=16$ ， 因为上面的数只有 $8$ 个，所以当 $i$ 超过了 $8$ 就停止操作了。
代码实现如下：

void update(int k, int x) // x 为数组 a[k] 所需要增加的量
{
	for (int i = k; i <= n; k++) Bit[i] += x;
}

例子如下：

#include

const int MAXN = 15;
int num[MAXN];
int Bit[MAXN];

int lowbit(int x)
{
	return x & -x;
}

void update(int k, int x)
{
	for (int i = k; i <= 8; i += lowbit(i)) Bit[i] += x;
}

int main()
{
	for (int i = 1; i <= 8; i++)
	{
		num[i] = i;
		update(i, num[i]); // num[i] 初值为 0 , 所以 num[i] = i 等于 num[i] += i
	}
	for (int i = 1; i <= 8; i++)
		printf("%d ", Bit[i]);
	return 0;
}

输出：
1 3 3 10 5 11 7 36

3. 有了 树状数组 怎么求 前缀和 ?

同样的，在上面 $lowbit$ 可以发现一个规律。 $Pre[i]$ 是前 $i$ 个数的前缀和，而 $Pre[i]$ 与 $Bit[]$ 的关系，就如下面所示：

int lowbit(int x)
{
	return x & (-x);
}

int Pre(int k)
{
	int pre = 0;
	for (int i = k; i > 0; i -= lowbit(i)) pre += Bit[i];
	return pre;		
}

有了这些算法，就可以解出之前的问题了，这样的算法也不会超时，这就是树状数组的优点。

---

$未完结哦$~