助你深刻理解——最长公共子串、最长公共子序列(应该是全网数一数二的比较全面的总结了)
往事不堪回首,那些年处理过的字符串【的一些骚操作】
- 最长公共子串篇(20191120)
- 理论知识:
- 图形理解:
- 矩阵初始化:
- 矩阵数值演变:
- 类似算法:
- 代码实现(C++):
- 代码设计满足的要求:
- 测试样例:
- 代码理解:
- 说说题目(理解进阶):
- 代码优化/美化版本补充:
- 最长公共子序列篇(20191121)
- 理论知识
- 代码实现与初步理解:
- 测试样例强化理解
- 该矩阵对应的动态规划过程分析如下图:
- 换个路径走,就是另外一种结果:
- 路径选择
- 局限性的补充说明:
- 其他随意测试
- 代码精简版
- 再次测试
- 后记
- 代码优化(20191122)
- 二阶滚动数组优化物理存储空间
- 代码优化
- 代码实现(只求取长度)
- 测试样例
- 代码实现(最终版——另辟蹊径,通过递归实现路径回溯)
- 测试样例
- 路径回溯强化理解
- 图片理解(亲自动手,丰衣足食!)
- 再一次后记
- 纠正后的图片(最终版)
- 补充:暴力枚举法
- 知识拓展:
- 如果是 N 个字符串查找最长公共子序列呢?
- 进一步深入理解:如果是 N 个字符环呢?
最长公共子串篇(20191120)
理论知识:
推荐参考该博文:java实现字符串匹配问题之求两个字符串的最大公共子串
当然这篇也一样,看个人理解:求两个字符串的最长公共子串
图形理解:
矩阵初始化:
矩阵数值演变:
类似算法:
图论中的最短路径算法。
大致分有:迪杰斯特拉算法(Dijkstra)和弗洛伊德算法(Floyd)。
(对应着 贪心算法和动态规划 …… 别慌,名字起的高大尚并无影响理解。。。)
数据结构算法编程课、离散数学课、计算机网络课等都会涉及该算法。
本质都是化作矩阵,故线性代数一定要好好学。
最好的理解方式是什么:
亲自动手 —— 图解,自己手动在草稿纸上推演一遍(小矩阵即可)。
代码实现(C++):
太长时间没写C了,一入python差些找不着回头路(哈哈)
#include>不过建议多多学习、开拓视野
int** dp = new int *[row];
if (dp) {
for (int i = 0; i < row; ++i) {
dp[i] = new int[col];
}
}
// 初始化矩阵,全部置false(即首先默认字符串不相同,其后相同再+1)
// 此处是为了提醒学弟,注意学习 memset和fill的区别
for (int i = 0; i < row; ++i) {
/*for (int j = 0; j < col; ++j) {
dp[i][j] = 0;
}*/
fill(dp[i], dp[i] + col, 0); // 两种初始化方式
}
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
int iTemp = i, jTemp = j; // 临时变量
while (s1[iTemp] == s2[jTemp]) {
dp[iTemp][jTemp] = dp[iTemp][jTemp] + 1;
sameSubString += s1[iTemp];
iTemp++;
jTemp++;
// 横纵都 +1是为了斜对角线(即 s1和s2串都往后移动一位)
// 值得注意的是别造成数组越界(程序健壮性问题、bug)
if (iTemp == row || jTemp == col) {
break;
}
}
// 相同子串不为空(即存在时)
if (!sameSubString.empty()) {
//cout << "sameSubString = " << sameSubString << endl; // 通过输出测试结果,是否如预期所想
if (IsNoRepetition(sameSubString, sameSubStringVector)) {
sameSubStringVector.push_back(sameSubString);
}
sameSubString.clear(); // 每遍历过一次相同子串,最后记得重置为空(细节)
}
}
}
// 矩阵变换完成后,查找最大值(即为最长相同子串长度)
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (max < dp[i][j]) {
max = dp[i][j];
}
}
}
if (sameSubStringVector.empty()) {
cout << endl;
}
else {
// 将各个相同子串按照字典顺序排序
sort(sameSubStringVector.begin(), sameSubStringVector.end());
for (VS::iterator iter = sameSubStringVector.begin(); iter != sameSubStringVector.end(); ++iter) {
// 直接输出的所有的相同子串
//cout << *iter << endl;
// 使用条件判断只输出最长的相同子串
if ((*iter).size() == max) {
cout << *iter << endl;
break; // break是为了只输出一个最长的公共子串,即ASCLL码最小的那个
}
}
}
//cout << endl; // 此空行是为了排版好看,避免pe格式出错
// 每执行一遍程序,重置为初始状态(为空)。至于,不放在else内,是编码经验释然。
sameSubStringVector.clear();
// new了内存空间就要delete
// 注意这种表达方式
for (int i = 0; i < row; ++i) {
delete[] dp[i];
}
delete[] dp;
}
return 0;
}
bool IsNoRepetition(string& str, vector<string>& vs) {
for (int i = 0; i < vs.size(); ++i) {
if (vs[i] == str)
return false; //有重
}
return true; //无重
}
代码设计满足的要求:
对于每组测试数据,输出最大子串。
如果最大子串为空(即不存在),则输出一个空行。
测试样例:
输入:
abcded123456aabbcc
abcdaa1234
输出:
1234
代码理解:
本人代码很平民化了,如果看了不能理解实在是……不敢恭维你的编程基础。
实在不理解的话,可以评论区留言或者私信本人账号。
当然,[email protected]发送邮件或者添加好友也可。只要笔者上线。
说说题目(理解进阶):
为何此处说即可理解最长公共子串、最长公共子序列?
因为只需要理解了理论知识部分(其实就是极其简单的逐个字符匹配问题),
代码只需要修改一个条件即可从最长相同子串转为最长相同子序列:
即对while (s1[iTemp] == s2[jTemp])循环进行相应的修改。
最长公共子串:字符一直匹配直到字符不再相同或者已经遍历完较短字符串;
最长公共子序列:一直遍历至较短字符串结束即可,当前字符不相同也要继续匹配下一对字符(各自向后挪动一位)
代码优化/美化版本补充:
由一道公共子串题目引起的自我反思
============ 我是分割线 ============
最长公共子序列篇(20191121)
理论知识
推荐博客:LCS(最长公共子序列)
讲解的很好了,以至于自己发现自己上边对最长公共子序列的理解过于想当然了。
上边的理解偏差在于:如何保证是在已有子序列的基础上去继续匹配下一对,这才是子序列的关键和难点。
代码实现与初步理解:
#include>不过建议多多学习、开拓视野;
// 先申请一列,该列的每个元素对应一个一维数组(一行);再每个元素位申请一行。(行、列都仅仅是指一维数组);
int** dp = new int *[row];
if (dp) {
for (int i = 0; i < row; ++i) {
dp[i] = new int[col];
}
}
// 初始化矩阵,全部置false(即首先默认字符串不相同,其后相同再+1)。注意学习 memset和fill的区别;
for (int i = 0; i < row; ++i) {
//dp[i][0] = 0; // 矩阵第一列全都置0
fill(dp[i], dp[i] + col, 0);
}
//for (int j = 0; j < col; ++j) {
// dp[0][j] = 0; // 矩阵第一行全部置0
//}
//printDP(dp, row, col);
// 注意内存空间范围,数组别越界了;
for (int i = 0; i < row - 1; ++i) {
for (int j = 0; j < col - 1; ++j) {
相等时,在已有的共同子序列的基础上,共同序列长度 +1;
对进行字符的比对时,记得 i、j 要 -1(即从开头起);
//if (s1[i] == s2[j]){
// dp[i + 1][j + 1] = dp[i][j] + 1;
//}
如何理解?——在已有序列的基础上,字串末尾添加不等的字符而已
//else {
// dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j]);
//}
// 若是只输出长度而不要求保存共同子序列的字符,则可以三目运算符(加括号是为了可读性、便于读者理解代码)
dp[i + 1][j + 1] = (s1[i] == s2[j] ? dp[i][j] + 1 : max(dp[i][j + 1], dp[i + 1][j]));
}
}
回溯,通过路径拼凑出LCS
int i = row - 1;
int j = col - 1;
while (i > 0 && j > 0) {
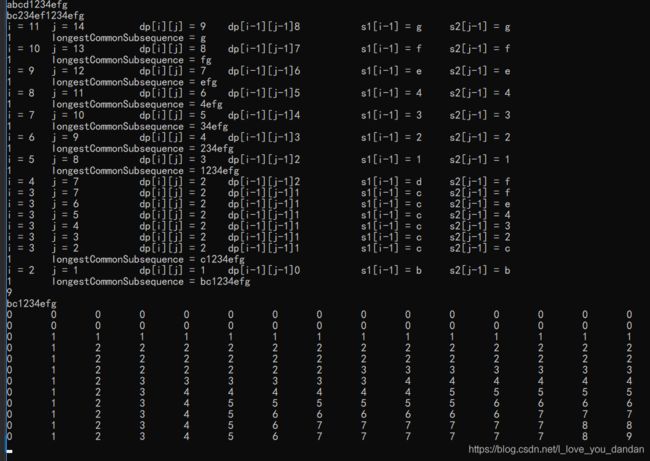
cout << "i = " << i << "\t" << "j = " << j << "\t\t";
cout << "dp[i][j] = " << dp[i][j] << "\t" << "dp[i-1][j-1]" << dp[i - 1][j - 1] << "\t\t";
cout << "s1[i-1] = " << s1[i - 1] << "\t" << "s2[j-1] = " << s2[j - 1] << endl;
if (dp[i][j] == dp[i - 1][j - 1] + 1 && s1[i - 1] == s2[j - 1]) {
if (i - 1 >= 0 && j - 1 >= 0) {
longestCommonSubsequence = s1[i - 1] + longestCommonSubsequence;
cout << "1" << "\t" << "longestCommonSubsequence = " << longestCommonSubsequence << endl;
}
--i;
--j;
// 走斜线(往左上方);
}
else if (dp[i - 1][j] > dp[i][j - 1]) {
if (i - 1 >= 0 && j - 1 >= 0 && s1[i - 1] == s2[j - 1]) {
longestCommonSubsequence = s1[i - 1] + longestCommonSubsequence;
cout << "2" << "\t" << "longestCommonSubsequence = " << longestCommonSubsequence << endl;
}
--i;
// 竖着走(往上);
}
else if (dp[i - 1][j] < dp[i][j - 1]) {
if (i - 1 >= 0 && j - 1 >= 0 && s1[i - 1] == s2[j - 1]) {
longestCommonSubsequence = s1[i - 1] + longestCommonSubsequence;
cout << "3" << "\t" << "longestCommonSubsequence = " << longestCommonSubsequence << endl;
}
--j;
// 横着走(往左);
}
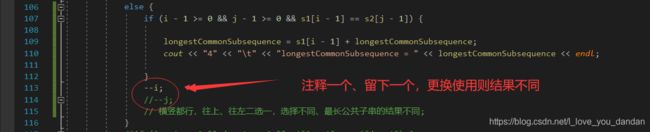
else {
if (i - 1 >= 0 && j - 1 >= 0 && s1[i - 1] == s2[j - 1]) {
longestCommonSubsequence = s1[i - 1] + longestCommonSubsequence;
cout << "4" << "\t" << "longestCommonSubsequence = " << longestCommonSubsequence << endl;
}
//--i;
--j;
// 横竖都行,往上、往左二选一,选择不同、最长公共子串的结果不同;
}
/*if (i - 1 >= 0 && j - 1 >= 0 && s1[i - 1] == s2[j - 1]) {
longestCommonSubsequence = s1[i - 1] + longestCommonSubsequence;
}*/
}
cout << dp[row - 1][col - 1] << endl;
cout << longestCommonSubsequence << endl;
printDP(dp, row, col);
// new了内存空间就要delete;
// 注意这种表达方式;
for (int i = 0; i < row; ++i) {
delete[] dp[i];
}
delete[] dp;
}
return 0;
}
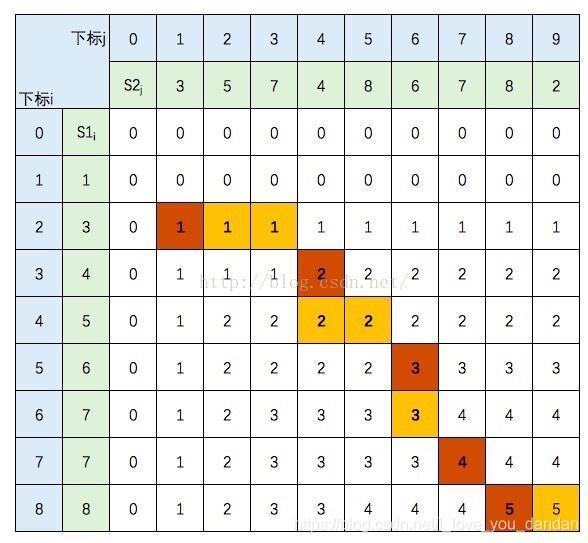
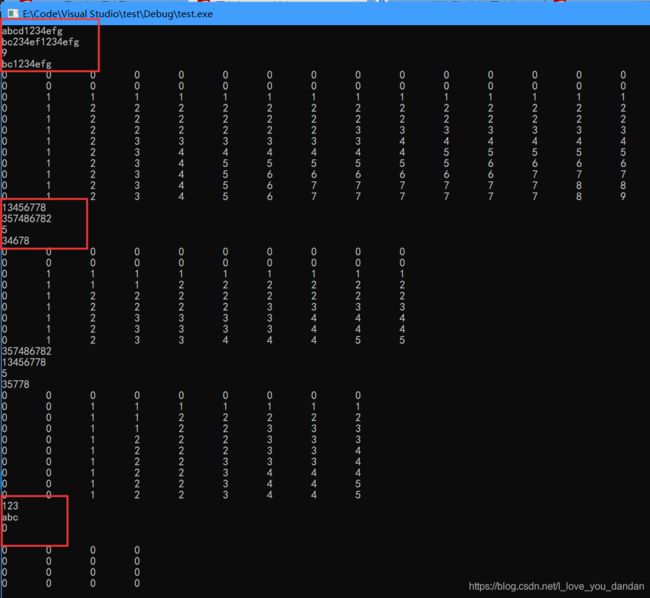
测试样例强化理解
该矩阵对应的动态规划过程分析如下图:
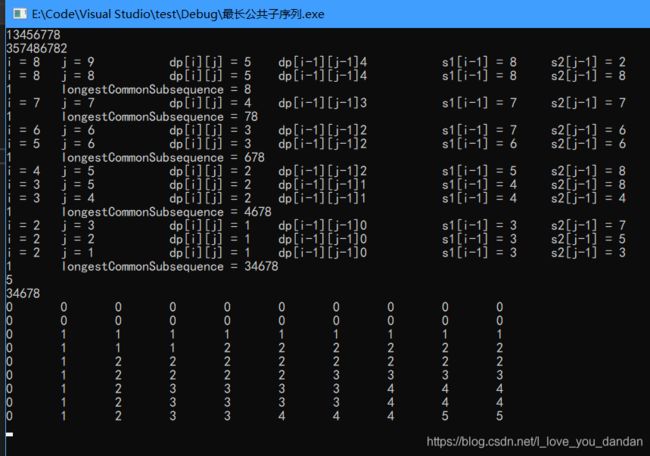
换个路径走,就是另外一种结果:
路径选择
局限性的补充说明:
(2019/11/24 21:11 补充)
动态规划实现的最长公共子序列的路径回溯,存在局限性 —— 只能选择边缘路径;
即:至多输出两种可能的最长公共子序列。
除非有人自己在横着走和竖着走都可行的那段代码,采用随机数选择法回溯路径。可是没有必要做这种费力又不讨好的无用功。
而路径回溯只能输出一个最长公共子序列,如果公共序列存在的话。
其他随意测试
代码精简版
#include再次测试
后记
亲自动手,丰衣足食。
2019/11/22 00:20
============ 我是分割线 ============
代码优化(20191122)
二阶滚动数组优化物理存储空间
代码优化
只求取最长公共子序列长度时,空间复杂度可从O(mn)降至O(min{m,n}),因为动态规划问题的本质仅仅是考虑:
dp[i][j]该 依据什么,从dp[i-1][j-1]、dp[i-1][j]和dp[i][j-1]三者中做出选择并生成自身数值;
其中:m,n为两字符串长度。
两行数组即可存储dp矩阵,实现动态滚动即可。
代码实现(只求取长度)
#include测试样例
代码实现(最终版——另辟蹊径,通过递归实现路径回溯)
#include测试样例
路径回溯强化理解
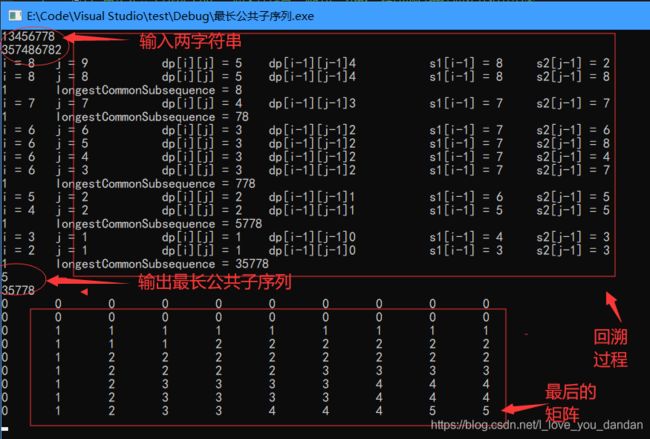
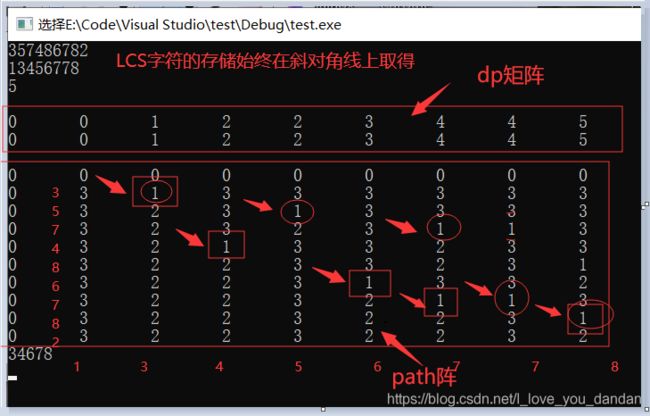
还是经典的测试样例:
357486782
13456778
两种路径两种结果:
横竖都可以走的时候,横着走:35778(下图中的椭圆)
竖着走:34678(下图中的小方块)
图片理解(亲自动手,丰衣足食!)
请忽略 path矩阵的第一行和第一列的全0数据;
剩下的,索引对应实现元素的回溯查找即可。
再一次后记
本来只是帮助大一学弟解答最长相同子串;演变成如此文章,岂非我本意。
不过,回过过往学习,还真的是、高度不一样了、理解也就更加深刻了。
经历过的人都会懂得的。
纠错:上图中,自左向右的倒数第二列的椭圆应该往下挪4个元素位。
纠正后的图片(最终版)
2019/11/22 19:24
以上纯属个人亲自测试结果,如有错误,可以评论区留言告知。
在此谢过!
转载请注明原文出处,再次感谢。
补充:暴力枚举法
二进制模拟串实现暴力破解——暴力枚举出(最长)公共子序列
2019/11/24 01:11
知识拓展:
如果是 N 个字符串查找最长公共子序列呢?
进一步深入理解:如果是 N 个字符环呢?
详情请看本人另外一篇子博客:
查找N个字符串(环)的最长公共子序列
如需转载,请注明出处!
https://blog.csdn.net/I_love_you_dandan/article/details/103173750
联系方式:[email protected]
欢迎各种友善交流。
2019/11/24 21:00