~最长递增子序列（LIS）~~~~树状DP

最长递增子序列问题（LIS）：给定一个长度为N的数组，找出一个最长的单调递增子序列。例如一个长度为7的序列A={5,6,7,4,2,8,3}，它最长的单调递增子序列为{5,6,7,8}，长度为4。注意：此处所说树状dp（树状数组优化的dp）并非树形dp。

LIS问题解决方法有很多，而树状DP是其中一种比较高效的方法，树状DP的实现要从基础DP开始。先引入一个模板题：

题目：“最少拦截系统”
某国有一种导弹拦截系统，这种导弹拦截系统有一个缺陷：虽然它的第1发炮弹能够到达任意高度，但是以后每一发炮弹都不能超过前一发的高度。某天，雷达捕捉到敌国的导弹来袭，请计算最小需要多少套拦截系统。
输入：导弹总个数，导弹依次飞来的高度。
输出：最少要配备多少套这种导弹拦截系统。
输入样例：
8 389 207 155 300 299 170 158 65
输出样例：
2

直接用DP求解LIS(复杂度O(n²))：
定义状态dp[ i ]，表示以第 i 个数为结尾的最长递增子序列的长度，那么：
dp[ i ] = max{0,dp[ j ]} +1，0ji
最后答案是max{dp( i )}。

#include
using namespace std;
const int N=1001;
int n,dp[N],p[N],res;
int LIS(){//动态规划 
	res=0;
	for(int i=1;i<=n;++i){
		for(int j=i;j>=1;--j){
			if(p[i]>p[j]||i==j)//最差自己成列 
				dp[i]=max(dp[j]+1,dp[i]);
		}
		res=max(dp[i],res); 
	}
	return res;
}
int main(){
	while(cin>>n){
		memset(p,0,sizeof(p));
		for(int i=1;i<=n;++i){
			cin>>p[i];
		}
		memset(dp,0,sizeof(dp));
		cout<<LIS()<<endl;
	}
	return 0;
}

树状DP（复杂度O(n*logn)）:
我们在递推数组dp的时候，需要不断地回头遍历数组本身，时间开销比较大了，那有没有办法减小这部分的时间开销呢？答案是肯定的，我们可以用树的结构来优化数据的处理，具体思路如下：
首先把每个数看成一个节点，每个节点都含两个属性(val(值)，cnt(序号)）,接着把这些节点按val排序得到新的序列，然后枚举所有节点的cnt，用树状DP处理（关键）。

#include 
using namespace std;
const int N=1001;
struct node{
	int cnt,val;
	inline friend bool operator<(const node &a,const node &b){
		return a.val==b.val?a.cnt>b.cnt:a.val<b.val;
	}
}p[N];
int n,dp[N],res;
int LIS(){//树状dp 
	res=0;
	for(int i=1;i<=n;++i){
		int x=p[i].cnt;
		for(int j=x;j;j-=(j&(-j))){//以它为尾的最长子序列  
			dp[x]=max(dp[j]+1,dp[x]);
		}
		for(int j=x;j<=n;j+=(j&(-j))){//刷新信息节点 
			dp[j]=max(dp[x],dp[j]);
		}
		res=max(dp[x],res);//更新结果 
	}
	return res;
}
int main(){
	while(cin>>n){
		for(int i=1;i<=n;++i){
			cin>>p[i].val;
			p[i].cnt=i;
		}
		sort(p+1,p+n+1);//按值排序 
		memset(dp,0,sizeof(dp));
		cout<<LIS()<<endl;
	}
	return 0;
} 

看完代码不要急，我们接着说树状DP是怎么处理信息的，这主要依靠两处循环代码

其一：

		for(int j=x;j;j-=(j&(-j))){//以它为尾的最长子序列  
			dp[x]=max(dp[j]+1,dp[x]);
		}

其二：

		for(int j=x;j<=n;j+=(j&(-j))){//刷新信息节点 
			dp[j]=max(dp[x],dp[j]);
		}

在这里我们先引入一个概念——信息点(01不相混的二进制数)
如图（被红线标记的节点）：
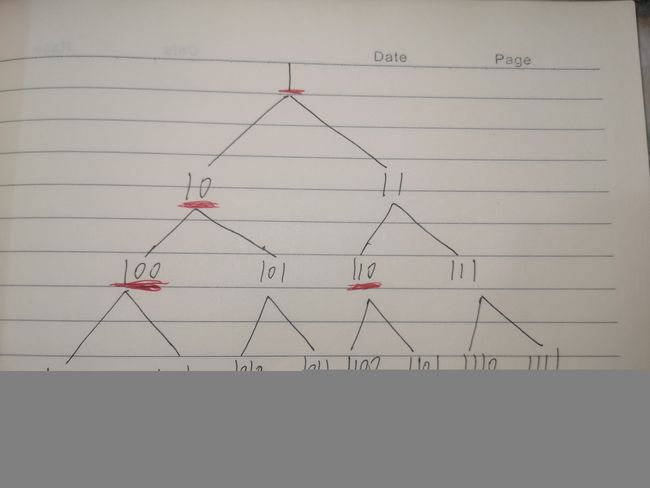我们已经定义了信息点，但还要再定义两个概念——大信息点(每行首个二进制数) 以及信息区（相邻两个信息点之间的区域），那这些信息点是干嘛的呢，其实有两个功能，功能一：接受其他节点传来的信息，功能二：供其他节点查询信息。

了解了这些以后，就可以进行解说了（重点）

在我们面前有两个问题要处理：
问题一：处在不同信息区的两个节点之间的信息传递问题。
问题二：处在同一个信息区的两个节点之间的信息传递问题。
（信息，表示加入新数据后最长递增子序长度，需要向后传递。）

前面说过了，把原序列通过val排序，然后我们按新序列来枚举每一个节点的cnt，我们用x代表cnt，x首先要通过第一处循环代码得到“以它结尾的最长上升子序列”，信息来源于它所在层并且二进制小于它的信息点，然后他会通过第二处循环代码把信息传给它所在层第一个二进制数大于它的信息点和所有二进制数大于它的大信息点，这就非常直观地解释了问题一。

而对于问题二又该怎么解释呢？其实已经解决了，我举个例子你就懂了，例子一:（10000~11000）10001,10010,10011,10100,10101,10110,10111.
这是其中一组处于同一信息区的二进制序列，如果我把这些数的前缀1全部消去不就是一个更小规模树状，那问题二和问题一就是同一个问题，问题就迎刃而解了。