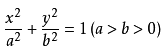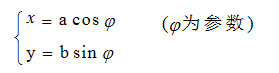cocos2dx之抽奖界面与获奖概率的设计(一)

****************************************************************************

时间：2015-02-01

作者：Sharing_Li

转载出处：http://blog.csdn.net/sharing_li/article/details/43268877

****************************************************************************

 

     

        在不同游戏中，经常有各种各样抽奖的环节，比如每次登入游戏的免费抽奖，卡牌游戏中的抽不同颜色的卡牌英雄，不同品质的武器抽奖，十连抽等等。今天给大家讲解一下，比较传统的抽奖方式，就是转转盘的抽奖，包含抽奖界面动画的设计和抽奖概率的设计。由于内容稍微有点多，所以分两篇进行讲解，本篇先介绍转盘抽奖方式的界面设计。废话不多说，先上效果图：

 

（。。。亮瞎了我的钛合金眼！）

来看看大致的功能需求有哪些：

    1、一个转盘，一个指针，可以是转盘转，也可以是指针转，本篇是转盘转。

    2、转盘在转的时候，速度是先快后慢，然后停止。

    3、转盘在转的时候，各种粒子效果的动画，其中包括圆环状的闪光星星，还有以椭圆轨迹运动的小彗星。

    4、抽中奖品后，弹出抽中奖品的动画。

 

看完功能需求，再来看看代码怎么写：

先看简单的初始化代码：

bool LotteryTurnTest::init()
{
	if (!Layer::init())
	{
		return false;
	}

	auto bgSize = Director::getInstance()->getWinSize();

	m_pBg = Sprite::create("LotteryTurn/bg_big.png");
	m_pBg->setPosition(Vec2(bgSize.width / 2,bgSize.height / 2));
	this->addChild(m_pBg);

	//添加标题
	auto plabel = Label::createWithTTF("LotteryTurnTest","fonts/Marker Felt.ttf",30);
	plabel->setPosition(Vec2(bgSize.width / 2,bgSize.height * 0.9));
	m_pBg->addChild(plabel);

	//添加转盘
	m_turnBg = Sprite::create("LotteryTurn/turn_bg.png");
	m_turnBg->setPosition(Vec2(bgSize.width / 2,bgSize.height / 2));
	m_pBg->addChild(m_turnBg);

	//添加指针
	auto arrNor = Sprite::create("LotteryTurn/turn_arrow.png");
	auto arrSel = Sprite::create("LotteryTurn/turn_arrow.png");
	arrSel->setColor(Color3B(190,190,190));
	m_turnArr = MenuItemSprite::create(arrNor,arrSel,CC_CALLBACK_1(LotteryTurnTest::onBtnCallback,this));
	m_turnArr->setPosition(Vec2(bgSize.width / 2,bgSize.height * 0.557));
	m_turnArr->setScale(0.7);
	auto pMenu = Menu::createWithItem(m_turnArr);
	pMenu->setPosition(Vec2::ZERO);
	m_pBg->addChild(pMenu);

	//添加中奖之后的简单界面
	auto awardLayer = LayerColor::create(Color4B(0,0,0,100));
	awardLayer->setPosition(Point::ZERO);
	awardLayer->setTag(100);
	m_pBg->addChild(awardLayer,10);
	awardLayer->setVisible(false);

	return true;
}

 

点击按钮，获取一个随机的旋转角度，转盘开始转，注意的是，转盘在转的时候，按钮要被设置成无效状态，以免多次点击。

//防止多次点击
	m_turnArr->setEnabled(false);

	srand(unsigned(time(NULL)));
	float angleZ = rand() % 720 + 720;
	auto pAction = EaseExponentialOut::create(RotateBy::create(4,Vec3(0,0,angleZ)));
	m_turnBg->runAction(Sequence::create(pAction,CallFunc::create(CC_CALLBACK_0(LotteryTurnTest::onTurnEnd,this)),NULL));

这里，我们用的EaseExponentialOut来控制转盘旋转的速度。

当然，转盘在转的时候，各种粒子效果开始行动啦，这里放到文章后面讲解，先看看中奖之后的动画：

//弹出抽中奖品
	((LayerColor *)m_pBg->getChildByTag(100))->setVisible(true);
	auto award = Sprite::create("LotteryTurn/award.png");
	award->setAnchorPoint(Vec2(0.5,0));
	award->setPosition(Vec2(m_pBg->getPositionX(),m_pBg->getPositionY() * 2));
	this->addChild(award);
	auto bounce = EaseBounceOut::create(MoveBy::create(2,Vec2(0,-m_pBg->getPositionX() * 2)));
	award->runAction(Sequence::createWithTwoActions(bounce,CallFuncN::create([=](Node * node){
					award->removeFromParentAndCleanup(true);
					((LayerColor *)m_pBg->getChildByTag(100))->setVisible(false);
					m_turnArr->setEnabled(true);
	})));

再来看看咱们转盘中的粒子效果，有两种，第一种圆环的星星闪烁效果比较简单，设置下离中心的距离就好了，这里主要讲解以椭圆轨迹旋转的小彗星粒子效果。

既然以椭圆为轨迹，其实也就是实时更新下粒子的位置，但是椭圆的坐标怎么计算呢？想必部分人都忘记了吧（我也忘记了。。。），直接去问度娘吧：

咱们椭圆的中心即是转盘的中心，所以是一个标准的椭圆方程：

，对应的参数方程就是：

那么答案就出来啦，只要我们实时改变参数φ的值，那么椭圆上的坐标就会实时更新。知道原理了，我们再来看看怎么设计这样一个椭圆类。既然沿椭圆轨迹运动，那么为什么不把这一种动作设计成跟cocos2dx引擎中的动作Action一样呢？在使用的时候，我们只需要调用runAction就可以了。我们可以参考cocos2dx引擎动作类的设计。

来看头文件：

#ifndef _ELLIPSEBY_H_
#define _ELLIPSEBY_H_

#include "cocos2d.h"

USING_NS_CC;

#define PI 3.14159

//椭圆的参数信息
struct EllipseConfig 
{
	//椭圆a的长度
	float ellipseA;
	//椭圆b的长度
	float ellipseB;
	//椭圆的中心坐标
	Vec2 cenPos;
	//是否逆时针旋转
	bool isAntiClockwise;
	//目标开始旋转的位置，默认位置是在椭圆长轴右方,即值为0
	float startAngle;
	//目标自身的角度
	float selfAngle;
};

class EllipseBy : public ActionInterval
{
public:
	EllipseBy();
	~EllipseBy();

	//初始化函数，参数t为持续时间，config为椭圆参数
	static EllipseBy * create(float t,const EllipseConfig & config);
	bool initWithDuration(float t,const EllipseConfig & config);

	//每帧更新当前椭圆坐标
	virtual void update(float time) override;
	//在动作开始前调用
	virtual void startWithTarget(Node *target) override;
	//动作的拷贝
	virtual EllipseBy * clone() const override;
	//动作的逆序
	virtual EllipseBy * reverse() const override;

protected:
	//获得椭圆上当前点坐标
	inline Vec2 getPosWithEllipse(float t)
	{
		float angle = 2 * PI * ((m_config.isAntiClockwise ? t : (1 - t)) + m_config.startAngle / 360);
		return Vec2(m_config.ellipseA * cos(angle),m_config.ellipseB * sin(angle));
	}

private:
	EllipseConfig m_config;
};

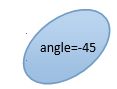
#endif

我们定义了一个椭圆参数的结构体EllipseConfig，前面4个比较好理解，后面2个：startAngle是开始旋转粒子出现的位置，值为角度值。比如下面例图所示：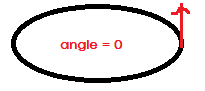

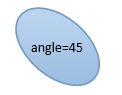
selfAngle是指把整个椭圆当成一个整体，这个整体的角度，类似于精灵的rotation属性。比如下面例图所示：

 接着再来看看从父类继承来的三个函数：startWithTarget、clone、reverse

startWithTarget是用来设置是谁要执行动作，在动作开始前调用；后面两个，一个是动作的拷贝，一个是动作的逆序，因为在父类中是纯虚函数，所以要继承实现。

再来看看函数getPosWithEllipse，这个是利用椭圆的参数方程，获得当前目标所处椭圆上的位置。因为要不停的调用，所以声明为内联函数。

最后看看cpp文件的部分实现代码：

EllipseBy * EllipseBy::clone() const
{
	auto pAction = new EllipseBy();
	pAction->initWithDuration(_duration, m_config);
	pAction->autorelease();
	return pAction;
}

EllipseBy * EllipseBy::reverse() const
{
	EllipseConfig resConfig = m_config;
	resConfig.isAntiClockwise = !m_config.isAntiClockwise;
	return EllipseBy::create(_duration, m_config);
}

void EllipseBy::startWithTarget(Node *target)
{
	ActionInterval::startWithTarget(target);
}

void EllipseBy::update(float time)
{
	if (_target)
	{
		Vec2 curPos = this->getPosWithEllipse(time);
		float tmpAngle = m_config.selfAngle / 180 * PI;
		float newX = curPos.x * cos(tmpAngle) + curPos.y * sin(tmpAngle);
		float newY = curPos.y * cos(tmpAngle) - curPos.x * sin(tmpAngle);
		_target->setPosition(m_config.cenPos + Vec2(newX,newY));
	}
}

其中最重要的部分就是update函数啦，getPosWithEllipse获得的坐标curPos是selfAngle为0时的坐标，如果我们设置了椭圆自身的角度，就要调整下curPos的坐标。有以下公式：

如果椭圆自身旋转了β，即selfAngle = β 那么之后的坐标是：newX = xcosβ + ysinβ，newY = ycosβ - xsinβ

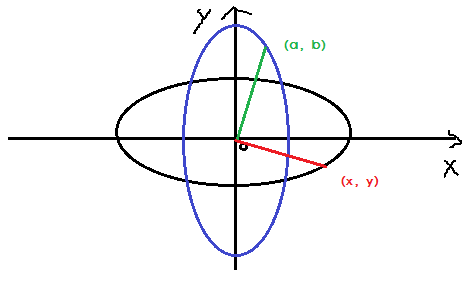
这里给大家简单的分析一下公式，先看图：

这里黑色的椭圆是没有设置selfAngle时的样子，当设置selfAngle为β后，就变成蓝色的椭圆。由于两个椭圆的中心都是圆心，所以椭圆上同一位置上的点到圆心的距离以一样，也就是上图中红线和绿线的长度相等，那么利用勾股定理，就是下面：

a^2 + b^2 = x^2 + y^2 = x^2 * 1 + y^2 * 1

因为cos& * cos& + sin& * sin& = 1，所以：

上面公式 = x^2 * (cos(β)^2 + sin(β)^2) + y^2 * (cos(β)^2 + sin(β)^2)

然后分解合并，就可以得到下面的公式啦：

a^2 + b^2 = (xcosβ + ysinβ)^2 + (ycosβ - xsinβ)^2

所以：a = xcosβ + ysinβ，b = ycosβ - xsinβ

 

最后，我们只需要如下调用，就可以像使用引擎的动作一样：

//椭圆旋转
	EllipseConfig config;
	config.ellipseA = 100;
	config.ellipseB = 50;
	config.cenPos = m_turnBg->getPosition();
	config.isAntiClockwise = true;
	config.startAngle = 0;
	config.selfAngle = 45;

	m_pElliRtt_1->runAction(RepeatForever::create( EllipseBy::create(2.5,config)));

到这里，本篇上部分内容已经讲解完了，下一篇将讲解抽奖概率的设计。

 资源下载处：http://download.csdn.net/detail/sharing_li/8414387

本篇第二篇地址：http://blog.csdn.net/sharing_li/article/details/43405569