1.翻转链表
链表的定义
public class MyNode {
private MyNode next;
private T data;
public int compare(MyNode n){
if(this.data.compareTo(n.data)>0){
return 1;
}
else if(this.data.compareTo(n.data)==0){
return 0;
}
else{
return -1;
}
}
public MyNode getNext() {
return next;
}
public void setNext(MyNode next) {
this.next = next;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
}
翻转
public MyNode reverse(MyNode head){
if(head==null){
return null;
}
MyNode pre=head;
MyNode cur=pre.getNext();
while(cur!=null){
MyNode next=cur.getNext();
cur.setNext(pre);
pre=cur;
cur=next;
}
head.setNext(null);//断开原来方向的链表
return pre;
}
- 快慢指针找链表 的中间位置
/**
*
* @param head
* @return
*Description:找有序链表的中间位置的前驱
*/
public MyNode getPreOfMid(MyNode head){
MyNode fast=head;
MyNode slow=head;
MyNode pre=head;
while(fast!=null && fast.getNext()!=null){
pre=slow;
slow=slow.getNext();
fast=fast.getNext().getNext();
}
//System.out.println(slow.getData());
return pre;
}
3.有序链表的合并
public MyNode Merge(MyNode list1, MyNode list2){
if(list1==null && list2==null){
return null;
}
else if(list1==null && list2!=null){
return list2;
}
else if(list1!=null && list2== null){
return list1;
}
MyNode head=new MyNode();
MyNode cur=head;
while(list1!=null&&list2!=null){
if(list1.compare(list2)<=0){
cur.setNext(list1);
list1=list1.getNext();
}
else if(list1.compare(list2)>0){
cur.setNext(list2);
list2=list2.getNext();
}
// else if(list1.compare(list2)==0){//
// cur.setNext(list1);
// list1=list1.getNext();
// cur=cur.getNext();
// cur.setNext(list2);
// list2=list2.getNext();
// }
cur=cur.getNext();
}
if(list1!=null){
cur.setNext(list1);
}
if(list2!=null){
cur.setNext(list2);
}
return head.getNext();
}
4.判断链表中是否有环
解法1: 借助额外的存储空间判断链表中是否有环
/*
* 借助额外的存储空间判断链表中是否有环
*/
public boolean hasCircle(MyNode head){
if(head==null || head.getNext()==null){
return false;
}
Set nodeSet=new HashSet<>();
MyNode cur=head;
while(cur!=null){
if(!nodeSet.contains(cur)){
nodeSet.add(cur);
cur=cur.getNext();
}
else{
return true;
}
}
return false;
}
解法2:不借助额外的存储空间,使用快慢指针判断链表中是否有环
/**
*
* @param head
* @return
*Description: 不借助额外的存储空间,使用快慢指针判断链表中是否有环
*/
public boolean hasCircleWithPointer(MyNode head){
if(head==null || head.getNext()==null){
return false;
}
MyNode slow=head;
MyNode fast=head;
while(fast!=null && fast.getNext()!=null){
slow=slow.getNext();
fast=fast.getNext().getNext();
if(fast==slow){
return true;
}
}
return false;
}
5.找出链表中环开始的地方
解法1:
public MyNode detectCycle(MyNode head){
if(head==null || head.getNext()==null){
return null;
}
Set nodeSet=new HashSet<>();
MyNode cur=head;
while(cur!=null){
if(!nodeSet.contains(cur)){
nodeSet.add(cur);
cur=cur.getNext();
}
else{
return cur;
}
}
return null;
}
解法2:
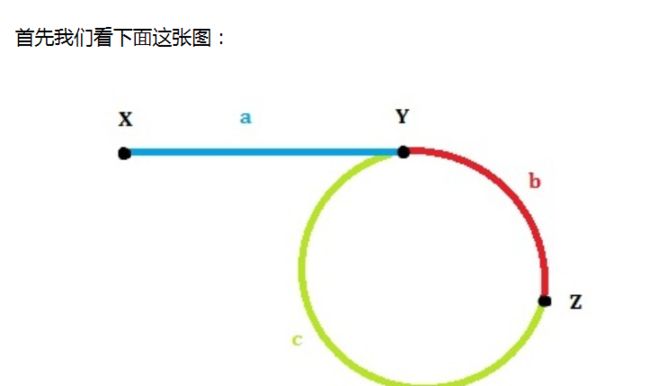
设:链表头是X,环的第一个节点是Y,slow和fast第一次的交点是Z。各段的长度分别是a,b,c,如图所示。环的长度是L。slow和fast的速度分别是qs,qf。
第一次相遇时slow走过的距离:a+b,fast走过的距离:a+b+c+b。
因为fast的速度是slow的两倍,所以fast走的距离是slow的两倍,有 2(a+b) = a+b+c+b,可以得到a=c(这个结论很重要!)。
我们发现L=b+c=a+b,也就是说,从一开始到二者第一次相遇,循环的次数就等于环的长度。
public MyNode detectCycleWithPointer(MyNode head){
if(head == null ||head.getNext()==null){
return null;
}
else{
MyNode fast=head;
MyNode slow=head;
while(fast!=null && fast.getNext()!=null){
slow=slow.getNext();
fast=fast.getNext().getNext();
if(fast==slow){
break; //第一次相遇在Z点
}
}
if(fast==null ||fast.getNext()==null){
return null;//无环
}
slow=head;//slow从头开始走,
while(slow!=fast){ //二者相遇在Y点,则退出
slow=slow.getNext();
fast=fast.getNext();
}
return slow;
}
}
6.如何将有环的链表变成单链表(解除环)?
解法1:
public MyNode releaseCycle(MyNode head){
if(head == null || head.getNext()==null){
return head;
}
else{
Set nodes=new HashSet<>();
MyNode cur=head;
MyNode pre=head;
while(cur!=null){
if(!nodes.contains(cur)){
nodes.add(cur);
pre=cur;
cur=cur.getNext();
}
else{
pre.setNext(null);
break;
}
}
return head;
}
}
解法2:
public MyNode releaseCycleWithPointer(MyNode head){
if(head == null ||head.getNext()==null){
return head;
}
else{
MyNode fast=head;
MyNode slow=head;
while(fast!=null && fast.getNext()!=null){
slow=slow.getNext();
fast=fast.getNext().getNext();
if(fast==slow){
break; //第一次相遇在Z点
}
}
if(fast==null ||fast.getNext()==null){
return head;//无环
}
slow=head;//slow从头开始走,
MyNode pre=null;
while(slow!=fast){ //二者相遇在Y点,则退出
pre=fast;
slow=slow.getNext();
fast=fast.getNext();
}
pre.setNext(null);
return head;
}
7.两个链表的第一个公共结点
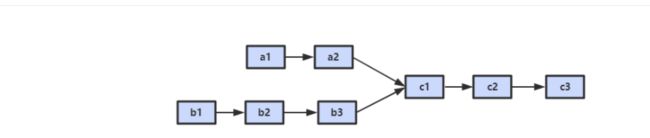
解题思路:设 A 的长度为 a + c,B 的长度为 b + c,其中 c 为尾部公共部分长度,可知 a + c + b = b + c + a。
当访问 A 链表的指针访问到链表尾部时,令它从链表 B 的头部重新开始访问链表 B;同样地,当访问 B 链表的指针访问到链表尾部时,令它从链表 A 的头部重新开始访问链表 A。这样就能控制访问 A 和 B 两个链表的指针能同时访问到交点。
public MyNode interception(MyNode n1,MyNode n2){
if(n1==null && n2==null){
return null;
}
else if(n1==null && n2!=null){
return n2;
}
else if(n1!=null && n2==null){
return n1;
}
else {
MyNode p1=n1;
MyNode p2=n2;
while(p1!=p2){
p1=p1.getNext()==null?n2:p1.getNext();
p2=p2.getNext()==null?n1:p2.getNext();
}
System.out.println(p1.getData()+"."+p2.getData());
return p1;
}
}
8.在 O(1) 时间内删除链表节点
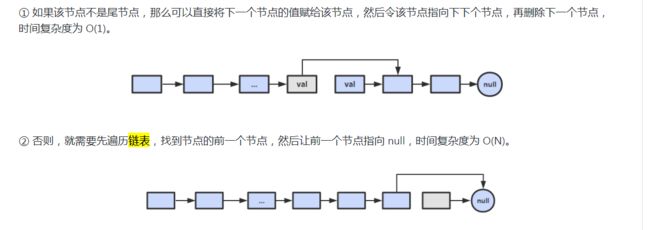
思路:
综上,如果进行 N 次操作,那么大约需要操作节点的次数为 N-1+N=2N-1,其中 N-1 表示 N-1 个不是尾节点的每个节点以 O(1) 的时间复杂度操作节点的总次数,N 表示 1 个尾节点以 O(N) 的时间复杂度操作节点的总次数。(2N-1)/N ~ 2,因此该算法的平均时间复杂度为 O(1)。
public MyNode deleteNode(MyNode head,MyNode dltNode){
if(head==null || head.getNext()==null||dltNode==null){
return head;
}
else{
if(dltNode.getNext()!=null){
dltNode.setData(dltNode.getNext().getData());
dltNode.setNext(dltNode.getNext().getNext());
}
else{
MyNode p=head;
MyNode pre=head;
while(p!=dltNode){
pre=p;
p=p.getNext();
}
pre.setNext(null);
}
return head;
}
}
-
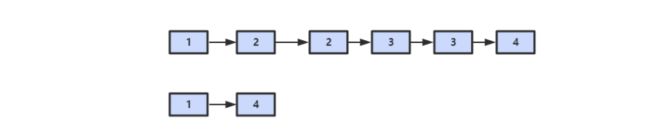
删除链表中重复的结点
public MyNode deleteDuplicate(MyNode head)
{
if(head==null || head.getNext()==null){
return head;
}
else{
MyNode next=head.getNext();
if(head.getData()==next.getData()){
while(next!=null && next.getData()==head.getData()){
next=next.getNext();
}
return deleteDuplicate(next);
}
else{
head.setNext(deleteDuplicate(next));
return head;
}
}
}
10.删除链表里倒数第K个节点
public MyNode reverseRecursive(MyNode head){
if(head == null || head.getNext()==null){
return head;
}
MyNode next=head.getNext();
head.setNext(null);
MyNode newHead=reverseRecursive(next);
next.setNext(head);
return newHead;
}
public MyNode getK(MyNode head,int k){
if(head==null || k<0){
return null;
}
MyNode newHead=reverseRecursive(head);
MyNode p=newHead;
int count=1;
while(k!=count){
p=p.getNext();
count++;
}
return p;
}
10.Given a singly linked list, determine if it is a palindrome.
Follow up:
Could you do it in O(n) time and O(1) space?
public boolean isPalindrome(ListNode head){
if(head==null || head.getNext()==null){
return true;
}
Stack stack=new Stack();
ListNode slow=head;
ListNode fast=head;
stack.push(head.getValue());
while(fast.getNext()!=null && fast.getNext().getNext()!=null){
slow=slow.getNext();
fast=fast.getNext().getNext();
stack.push(slow.getValue());
}
if(fast.getNext()!=null){
slow=slow.getNext();
}
while(slow!=null){
if(slow.getValue()!=stack.pop()){
return false;
}
slow=slow.getNext();
}
return true;
}
上述解法借助栈,空间复杂度不是O(1)
下面解法,借助快慢指针,找到中间位置后,翻转链表。然后前半部分和后半部分进行比较
public ListNode reverseList(ListNode head){
if(head==null || head.getNext()==null){
return head;
}
ListNode next=head.getNext();
head.setNext(null);
while(next!=null){
ListNode tmpNode=next.getNext();
next.setNext(head);
head=next;
next=tmpNode;
}
return head;
}
public boolean isPalin(ListNode head){
if(head==null || head.getNext()==null){
return true;
}
ListNode fast=head;
ListNode slow=head;
while(fast.getNext()!=null && fast.getNext().getNext()!=null){
slow=slow.getNext();
fast=fast.getNext();
}
ListNode newHead=reverseList(slow.getNext());
ListNode cur=head;
while(slow!=null){
if(cur.getValue()!=newHead.getValue()){
return false;
}
cur=cur.getNext();
slow=slow.getNext();
}
return true;
}
Sort a linked list in O(n log n) time using constant space complexity.
因为题目要求复杂度为O(nlogn),故可以考虑归并排序的思想。
归并排序的一般步骤为:
1)将待排序数组(链表)取中点并一分为二;
2)递归地对左半部分进行归并排序;
3)递归地对右半部分进行归并排序;
4)将两个半部分进行合并(merge),得到结果。
public ListNode mergeList(ListNode head){
if(head == null || head.getNext()==null){
return head;
}
ListNode preMid=getMid(head);
ListNode mid=preMid.getNext();
preMid.setNext(null);
return mergeSort(mergeList(head),mergeList(mid));
}
/**
* @param mergeList
* @param mergeList2
* @return
*Description:
*/
private ListNode mergeSort(ListNode node1, ListNode node2) {
if(node1== null && node2 !=null)
{
return node2;
}
if(node1!=null && node2==null){
return node1;
}
if(node1==null && node2==null){
return null;
}
ListNode head=new ListNode();
ListNode cur=head;
while(node1!=null && node2!=null){
if(node1.compare(node2)>=0){
cur.setNext(node2);
node2=node2.getNext();
}
else{
cur.setNext(node1);
node1=node1.getNext();
}
cur=cur.getNext();
}
if(node1!=null){
cur.setNext(node1);
}
else if(node2!=null){
cur.setNext(node2);
}
return head.getNext();
}
/**
*
* @param node1
* @param node2
* @return
*Description:功能同上
*/
private ListNode mergeSort2(ListNode node1, ListNode node2){
ListNode head;
if(node1.compare(node2)<=0){
head=node1;
node1=node1.getNext();
}
else{
head=node2;
node2=node2.getNext();
}
ListNode cur=head;
while(node1!=null && node2!=null){
if(node1.compare(node2)<=0){
cur.setNext(node1);
node1=node1.getNext();
}
else{
cur.setNext(node2);
node2=node2.getNext();
}
cur=cur.getNext();
}
if(node1!=null){
cur.setNext(node1);
}
else if(node2!=null){
cur.setNext(node2);
}
return head;
}
/**
* @param head
* @return 1-2-3-4
*Description:
*/
private ListNode getMid(ListNode head) {
if(head ==null || head.getNext()==null){
return head;
}
ListNode fast=head;
ListNode slow=head;
while(fast.getNext()!=null && fast.getNext().getNext()!=null){
slow=slow.getNext();
fast=fast.getNext().getNext();
}
return slow;
}
- 插入排序的基本思想:将一个节点插入到一个有序的序列中。对于链表而言,要依次从待排序的链表中取出一个节点插入到已经排好序的链表中,也就是说,在单链表插入排序的过程中,原链表会截断成两部分,一部分是原链表中已经排好序的节点,另一部分是原链表中未排序的节点,这样就需要在排序的过程中设置一个当前节点,指向原链表未排序部分的第一个节点。
注意单链表插入排序和数组插入排序的不同:数组插入排序是从排好序的部分的最后一个节点往前找,找到第一个比它小的数,然后插到其后面;而单链表只能从前往后遍历,找到第一个比当前节点大的值结束,因此在遍历已经排好序的链表部分的时候,需要两个指针,一个指针用于往前遍历(该指针假设为遍历指针),一个指针用于记录遍历指针指向的当前节点的前一个节点(该指针假设为遍历指针),这样当遍历指针找到第一个比待插入节点的值大的节点的时候,就可以将待插入节点插入到记录指针的后面。(之所以使用两个指针,是因为单链表不能反指)
插入排序分两种情况,一种是当前节点的值比已经排好序的尾节点的值大,则直接将当前节点挂在已排序的节点即可;一种是当前节点值比已经排好序的尾节点的值小,则需将已排好序的链表部分从头到尾遍历,找到第一个比当前节点值大的节点,插入到其前面即可。因为可能待插入的节点可能在第一个节点的前面,因此另外创建一个头结点,指向已经排好序的链表的第一个节点。这样可以每次插入新的节点的时候,将上面所提到的记录节点初始化为新创建的头结点,这样便于在第一个节点前面插入新节点。
/**
*
* @param head
* @return
*加入原始链表如下:1->8->2->5 ,排序过程如下
* newHeader->1->8
* newHead->1->2->8
* newHead->1->2->5->8
*/
public MyNode insertionSort(MyNode head){
if(head==null||head.getNext()==null){
return head;
}
MyNode newHead=new MyNode();//虚拟头节点,维护的是已排序元素的虚拟头节点
MyNode cur=head;//cur表示的是待排序节点的首节点
while(cur!=null){
MyNode pre=newHead;//每次都从头开始
MyNode tmp=cur.getNext();
while(pre.getNext()!=null && pre.getNext().compareTo(cur)<0){
pre=pre.getNext();
}
cur.setNext(pre.getNext());
pre.setNext(cur);
cur=tmp;
}
return newHead.getNext();
}
13.单链表的选择排序,要求空间复杂度为O(1).
/**
*
* @param head
* @return
*Description:空间复杂度O(1),选择排序。加入原始的列表2-4-9-5
*head可以理解为待存放最小位置的头节点,每次将最小的元素放在head所在的位置
*/
public MyNode selectionSort(MyNode head){
if(head==null || head.getNext()==null){
return head;
}
MyNode q=head;
MyNode p=head.getNext();
while(head!=null){
while(p!=null){
if(head.getData().compareTo(p.getData())>0){
int tmp=(Integer) head.getData();
head.setData(p.getData());
p.setData(tmp);
}
p=p.getNext();
}
head=head.getNext();
p=head;
}
return q;
}