0-1背包问题(动态规划)
测试用例与输出:
3 10
5 8
8 20
4 17
Case 1: 1 3 25思路:直接用动态规划DP凑出最优解,做动态规划一点要打印出递推矩阵,方便理解。
一、数据
n 为物品个数,m为背包重量,v数组存物品价值,w存物品重量
bag为dp递推矩阵第0行为全部初始化为0,isPush代表是否放入默认false
首先读入以上数据
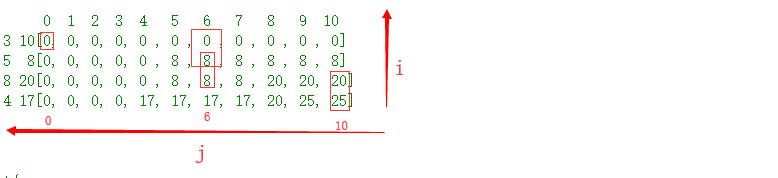
二、递推矩阵
0 1 2 3 4 5 6 7 8 9 10 ==> j
0 [0, 0, 0, 0, 0 , 0 , 0 , 0 , 0 , 0 , 0]
1 [0, 0, 0, 0, 0 , 8 , 8 , 8 , 8 , 8 , 8]
2 [0, 0, 0, 0, 0 , 8 , 8 , 8 , 20, 20, 20]
3 [0, 0, 0, 0, 17, 17, 17, 17, 20, 25, 25]
i
1、以(1,1)为起点,从左到右,从上到下遍历矩阵(递推),第0行,第0列为皆为0,代码如下
for (i = 1; i <= n; i++){//代表0~i件商品放入背包,n为最大商品数
for (j = 1; j <= m; j++){//代表背包容量,m为最大值
}
}助解:
当i=1时,代表第1件物品要放入背包,最后推出1件商品时,背包可以放下的最多价值。
当i=2时,代表前两件物品要放入背包,通过递推公式,最后推出前2件商品,背包可以放下的最多价值。
当i=3是,同理前3件物品。。。。
最后推出n件商品能放的最多价值
2、递推矩阵填充数据,在每一个bag[i][j],用以下递推公式
if (j < w[i])//当要放入的东西超出背包的容量
bag[i][j] = bag[i - 1][j];
else{
//bag[i - 1][j]当前背包的价值
//bag[i - 1][j - w[i]] 当前物品i未放入时的价值 + v[i] 当前物品i的价值 = 放入该件物品i后的价值
//当前背包的价值 > 放入该件物品i后的价值 ==> 不放
if (bag[i - 1][j] > bag[i - 1][j - w[i]] + v[i])
bag[i][j] = bag[i - 1][j];
else//放入之后背包价值变大 ==> 放入
bag[i][j] = bag[i - 1][j - w[i]] + v[i];
}最后得出得最递推矩阵,bag[n][m] 的值为最后能放的最大价值
3、判断放入那些物品,后bag[n][m]位置回溯,我们从递推矩阵发现,如果我们放入物品,第i行与第i-1行同一列的值不一样,此时j - w[i], 如果没放,则第i行与第i-1行同一列的值是一样的,j不变。每次都要i--,最后出口i=j=0(暂时想不出更好的讲法,下次想到再改改)
三、附上源代码
#include"iostream"
#define MAX_I 100
#define MAX_J 1000
using namespace std;
int main(){
int n, m, i, j;
int w[MAX_I];//weight 权重
int v[MAX_J];//value 价值
int bag[MAX_I][MAX_J];//动态规划用背包局座
bool isPush[MAX_I];//记录是否已经放入背包
int id = 1;
while (~scanf("%d %d", &n, &m)){
memset(bag, 0, sizeof(bag));//初始化第0行全部为0
memset(isPush, 0, sizeof(isPush));
for (i = 1; i <= n; i++){
scanf("%d %d", &w[i], &v[i]);
}
for (i = 1; i <= n; i++){
for (j = 1; j <= m; j++){
if (j < w[i])//当要放入的东西超出背包的容量
bag[i][j] = bag[i - 1][j];
else{
//bag[i - 1][j]当前背包的价值
//bag[i - 1][j - w[i]] 当前物品i未放入时的价值 + v[i] 当前物品i的价值 = 放入该件物品i后的价值
//当前背包的价值 > 放入该件物品i后的价值 ==> 不放
if (bag[i - 1][j] > bag[i - 1][j - w[i]] + v[i])
bag[i][j] = bag[i - 1][j];
else//放入之后背包价值变大 ==> 放入
bag[i][j] = bag[i - 1][j - w[i]] + v[i];
}
}
}
//由后往前回溯
for (i = n, j = m; i > 0; i--){
if (bag[i][j] != bag[i - 1][j]){//两行价值不一样,说明有放入东西
j -= w[i]; //扣除该物品重量
isPush[i] = true;
}
}
printf("Case %d:", id++);
for (i = 1; i <= n; i++){
if (isPush[i])
printf(" %d", i);
}
printf(" %d\n", bag[n][m]);
}
return 0;
}
/*
0 1 2 3 4 5 6 7 8 9 10
3 10[0, 0, 0, 0, 0 , 0 , 0 , 0 , 0 , 0 , 0]
5 8[0, 0, 0, 0, 0 , 8 , 8 , 8 , 8 , 8 , 8]
8 20[0, 0, 0, 0, 0 , 8 , 8 , 8 , 20, 20, 20]
4 17[0, 0, 0, 0, 17, 17, 17, 17, 20, 25, 25]
*/