NOIP竞赛学习整理--动态规划算法举例P1264

动态规划

什么是动态规划？

动态规划是解决多阶段决策最优化问题的一种思想方法。所谓“动态”，指的是在问题的多阶段决策中，按某一顺序，根据每一步所选决策的不同，将随即引起状态的转移，最终在变化的状态中产生一个决策序列。动态规划就是为了使产生的决策序列在符合某种条件下达到最优。

一、动态规划中的主要概念，名词术语

1 阶段：把问题分成几个相互联系的有顺序的几个环节，这些环节即称为阶段。
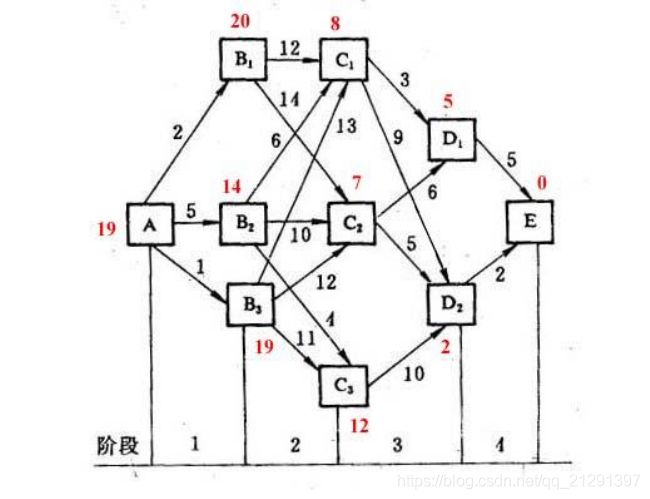
2 状态：某一阶段的出发位置称为状态。通常一个阶段包含若干状态。如图1中，阶段3就有三个状态结点4、5、6。
3 决策：从某阶段的一个状态演变到下一个阶段某状态的选择。
4策略：由开始到终点的全过程中，由每段决策组成的决策序列称为全过程策略，简称策略。
5 状态转移方程：前一阶段的终点就是后一阶段的起点，前一阶段的决策选择导出了后一阶段的状态，这种关系描述了由k阶段到k+1阶段状态的演变规律，称为状态转移方程。
6 目标函数与最优化概念：目标函数是衡量多阶段决策过程优劣的准则。最优化概念是在一定条件下找到一个途径，经过按题目具体性质所确定的运算以后，使全过程的总效益达到最优。

二、动态规划问题的数学描述

首先，例举一个典型的且很直观的多阶段决策问题:
[例] 下图表示城市之间的交通路网，线段上的数字表示费用，单向通行由
A->E。试用动态规划的最优化原理求出 A->E 的最省费用。

如图从 A 到 E 共分为 4 个阶段，即第一阶段从 A 到 B，第二阶段从 B 到 C，
第三阶段从 C 到 D，第四阶段从 D 到 E。除起点 A 和终点 E 外，其它各点既是上
一阶段的终点又是下一阶段的起点。例如从 A 到 B 的第一阶段中，A 为起点，终
点有 B1，B2，B3 三个，因而这时走的路线有三个选择，一是走到 B1，一是走到
B2，一是走到 B3。若选择 B2 的决策，B2 就是第一阶段在我们决策之下的结果，
它既是第一阶段路线的终点，又是第二阶段路线的始点。在第二阶段，再从 B2
点出发，对于 B2 点就有一个可供选择的终点集合(C1，C2，C3)；若选择由 B2
走至 C2 为第二阶段的决策，则 C2 就是第二阶段的终点，同时又是第三阶段的始
点。同理递推下去，可看到各个阶段的决策不同，线路就不同。很明显，当某阶
段的起点给定时，它直接影响着后面各阶段的行进路线和整个路线的长短，而后 面各阶段的路线的发展不受这点以前各阶段的影响。故此问题的要求是：在各个
阶段选取一个恰当的决策，使由这些决策组成的一个决策序列所决定的一条路
线，其总路程最短。

三、 运用动态规划需符合的条件

任何思想方法都有一定的局限性，超出了特定条件，它就失去了作用。同理，动态规划也并不是万能的。那么使用动态规划必须符合什么条件呢？必须满足最优化原理和无后效性。

1 最优化原理

最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状
态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。

2 无后效性

“过去的步骤只能通过当前状态影响未来的发展，当前的状态是历史的总结”。这条特征说明动态规划只适用于解决当前决策与过去状态无关的问题。状态，出现在策略任何一个位置，它的地位相同，都可实施同样策略，这就是无后效性的内涵。
由上可知，最优化原理，无后效性，是动态规划必须符合的两个条件。

四 、动态规划的计算方法

对于一道题，怎样具体运用动态规划方法呢？

（1）首先，分析题意，考察此题是否满足最优化原理与无后效性两个条件。
（2）接着，确定题中的阶段，状态，及约束条件。
（3）推导出各阶段状态间的函数基本方程，进行计算。

应用举例：数字三角形（洛谷-P1216）

题目描述
观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

    7 
  3   8 
8   1   0 

2 7 4 4
4 5 2 6 5
在上面的样例中,从 7 \to 3 \to 8 \to 7 \to 57→3→8→7→5 的路径产生了最大

输入格式
第一个行一个正整数 rr ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式
单独的一行,包含那个可能得到的最大的和。

输入输出样例
输入：
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出
30

思路：

@顺推：

F[i+1][j] = MAX (F[i][j] + a[i+1][j]);

F[i+1][j+1] = MAX (F[i][j] + a[i+1][j+1]);

@ 逆推：

F[i][j] = MAX (F[i-1][j], F[i-1][j-1]) + a[i][j]; (注意！逆推时要注意边界情况！ )

代码如下：
1、顺推：

//T2:数字金字塔-顺推（有点类似于记忆化搜索的思路）
//d数组储存顺序：记录从顶端向底部走的路径最优值（自顶向下）

#include
#include
using namespace std;
int a[1005][1005];//储存数塔
int d[1005][1005];//从该点到底端的最大数字和
int main()
{
    int i,j,n,ans;
    while(cin>>n)
    {
        memset(d,-1,sizeof(d));
        for(i=0;i<n;i++)
            for(j=0;j<=i;j++)
            {
                cin>>a[i][j];
            }
        d[0][0]=a[0][0];
        for(int i=0;i<n-1;++i)
        for(int j=0;j<=i;++j)//d数组为最优值路径（黑色金字塔，a为源数据数组（紫色金字塔）
        {
            //分别用最优值来更新左下方和右下方
            d[i+1][j]=max(d[i+1][j],d[i][j]+a[i+1][j]);//和当前的f[i+1][j]比较
            d[i+1][j+1]=max(d[i+1][j+1],d[i][j]+a[i+1][j+1]);//和当前的f[i+1][j+1]比较
        }
            //答案可能是最后一行的任意一个，所以把最后一行搜索一遍，最大的赋给ans
            ans=0;
            for(int i=0;i<n;i++)
            ans=max(ans,d[n-1][i]);
            cout<<ans<<endl;
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<=i;++j)
            {
                cout<<d[i][j]<<" ";
            }
            cout<<endl;
        }
    }
    return 0;
}

2、逆推

//数字金字塔-逆推
//d数组储存顺序：记录从顶端向底部走的路径最优值（自顶向下）
#include
#include
using namespace std;
int a[1005][1005];//储存数塔
int d[1005][1005];//从该点到底端的最大数字和
int main()
{
    int i,j,n,ans;
    while(cin>>n)
    {
        memset(d,-1,sizeof(d));
        for(i=0;i<n;i++)
            for(j=0;j<=i;j++)
            {
                cin>>a[i][j];
            }
        //逆推（自顶向下）
        d[0][0]=a[0][0];
        for(int i=1;i<n;i++)
        {
            d[i][0]=d[i-1][0]+a[i][0];//最左的位置没有左上方
            d[i][i]=d[i-1][i-1]+a[i][i];//最右的位置没有右上方
            for(int j=0;j<=i;j++)//在左上方和右上方取较大的
            d[i][j]=max(d[i-1][j-1],d[i-1][j])+a[i][j];
        }
        //答案可能是最后一行的任意一个，所以把最后一行搜索一遍，最大的赋给ans
        ans=0;
        for(int i=0;i<n;i++)
        ans=max(ans,d[n-1][i]);
        cout<<ans<<endl;;



        for(int i=0;i<n;++i)
        {
            for(int j=0;j<=i;++j)
            {
                cout<<d[i][j]<<" ";
            }
            cout<<endl;

        }
    }
    return 0;
}

附注：

动态规划相比较于深度搜索算法是一种高效算法。若能成功运用，必会使程序效率，无论时间还是空间，都有着质的飞跃。

掌握好动态规划，关键还是在于理解动态规划算法的基础上，多找一些相关的题进行练习。