使用一幅离轴干涉全息图重建相位

使用一幅离轴干涉全息图重建相位，这种方法是基于空间线性载频移相原理。
空间载频移相法原理如下文所示。
假设把一幅干涉图复制为4份，分别为t1,t2,t3,t4，在每一幅干涉图上采取一个像素点。这些像素点必须连续并且在同一周期内，例如t1上采取点(x,y)的像素，在t2采取点（x+1,y）的像素，在t3采取点(x+2,y)的像素，在t4采取点(x+3,y)的像素。因为这四个连续的像素点都在同一个周期内，他们都在周期上有对应的点，所以这四个点的光强值一一对应于四幅干涉图中的像素点的值。因此可以采用相应的公式计算出相位信息。这种方法的实质是把相位差从时域转化到空域中。

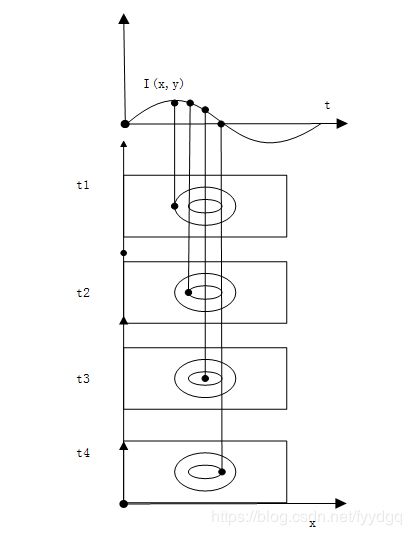
图3.3时域与空域采样点对应图
选用合适的采样运算公式，代入间隔区域里的连续像素点光强值就可以计算出一定点的相位值。而且间隔区域并不是一成不变的，可以选用不同的间隔区域，根据间隔区域的大小使用不同的相移采样运算公式。由于这些当计算出一点的相位后，可以把间隔区域向右移动一个像素，计算下一点的位相，如果一行运算完毕，就可以跳到下一行，依次类推，可以计算出整幅干涉全息图的相位值。
在第二章中，我们已经介绍了两种常见的针对离轴干涉全息图的相位提取算法，分别是傅里叶变换法和希尔伯特边变换法。这两种法检测过程的较复杂，计算量较大。于是，本文研究了基于空间载频相移技术的相位提取算法，这种算法的计算时间比傅里叶变换法和希尔伯特法要快得多而且计算结果近似相等。
在空间载频相移技术中，设一个离轴全息图为，


数值模拟程序
clc;
clear all;
close all;
pixel=1;
x=pixel*(-499:524);
y=pixel*(-499:524);
[xx,yy]=meshgrid(x,y);
d1=3pixel;
i=sqrt(-1);t=zeros(1024);t(350:400,300:700)=1.0;
ref=exp(i2pi(xx/d1)+ipi/2);
obj=exp(i(t));
A1=(ref+obj).*conj(ref+obj);
figure;imshow(A1,[]);
A2=A1(1:768,1:1024);
%title(‘模拟图’);
imwrite(A2,‘t17.bmp’)
%%%%%%%%%%%%%%%%%%%%%%%%%%
I=A2;
I11=imcrop(I,[1 1 1018 768]);
% figure;
% imshow(I11);
% title(‘图1’);
% I11=mat2gray(I11);
I22=imcrop(I,[2 1 1018 768]);
% figure;
% imshow(I22);
% title(‘图2’);
% I22=mat2gray(I22);
I33=imcrop(I,[3 1 1018 768]);
% figure;
% imshow(I33);
% title(‘图3’);
% I33=mat2gray(I33);

Deltaq=-atan2(tan(pi./3)(I11-I33),((I11)-2I22+I33));
imshow(Deltaq,[])
[y,x]=size(Deltaq);
i=sqrt(-1);
x=1:x;y=1:y;
[x,y]=meshgrid(x,y);

Deltaq1=angle(exp(iDeltaq).exp(-i2pi0.333333x+i2pi0.000001y));
imshow(Deltaq1,[]);
Q = unwrap(Deltaq1,pi./2);
imshow(Q,[]);
T=t(1:768,2:1020);
C=T+Q;
imshow(C,[])

MATLAB空间载频法程序
X=imread(‘I1.bmp’);
X=rgb2gray(X);
[m,n]=size(X);
Xnoised=imnoise(X,‘speckle’,0.00878);
figure;
imshow(Xnoised);
Y=dct2(Xnoised);
I=zeros(m,n);
I(1:m/3.13,1:n/3.13)=1;
Ydct=Y.*I;
Y=uint8(idct2(Ydct));

figure;
imshow(Y);
%%%%%%%%%%
I=Y
I11=imcrop(I,[1 1 1018 768]);
figure;
imshow(I11);
title(‘图1’);
I11=mat2gray(I11);
I22=imcrop(I,[2 1 1018 768]);
figure;
imshow(I22);
title(‘图2’);
I22=mat2gray(I22);
I33=imcrop(I,[3 1 1018 768]);
figure;
imshow(I33);
title(‘图3’);
I33=mat2gray(I33);

Deltaq=-atan2(tan(pi./6)(I11-I33),((I11)-2I22+I33));
#pi/6是原图上移动一个像素产生的相位差
[y,x]=size(Deltaq);

i=sqrt(-1);
x=1:x;y=1:y;
[x,y]=meshgrid(x,y);

Deltaq1=angle(exp(iDeltaq).exp(-i2pi0.14836x+i2pi0.00399y));
imshow(Deltaq1,[])

Q = unwrap(Deltaq1,pi/2);
imshow(Q,[]);