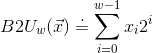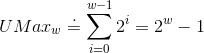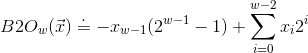信息的表示和处理

int32_t 和 int64_t 分别为4个字节和8个字节，数据大小固定，不随编译器和机器设置而变化。

在内存中按照从最低有效字节到最高有效字节的顺序存储对象，小端法。

按照从最高有效字节到最低有效字节的顺序存储对象，大端法。

文本数据比二进制数据具有更强的平台独立性。二进制代码是不兼容的，很少能在不同机器和操作系统组合之间移植。

在整数运算中，每个值x有一个加法逆元-x，使得x+(-x)=0。布尔环，加法逆元是它自身，“+”号是^异或。a^a=0,(a^b)^a=b.

位向量的一个很有用的应用是表示有限集合。可以用位向量编码任何子集,其中当且仅当。布尔运算的|和&对应集合的并和交，~对应集合的补。

位级运算的一个常见用法是实现掩码运算，这里掩码是一个位模式，表示从一个字中选出的位的集合。

 

移位运算。左移，丢弃最高k位，右端补k个0.

右移，分为逻辑右移和算术右移。逻辑右移在左端补k个0,算术右移补k个最高有效位的值。

C语言标准没有明确定义有符号数应该使用哪种右移。几乎所有编译器是算术右移。对无符号数，右移必须是逻辑的。

当移位量k大于等于位数w时，

int lval = 0xFEDCBA98 <<32;
int aval = 0xFEDCBA98 >>36;
unsigned uval = 0xFEDCBA98u >>40;

因为实际位移量是通过 k mod w得到的，所以上面三个的移位0,4,8位。

对C程序应该保持移位量小于位数。

 

无符号数的编码：

原理：无符号数编码的定义，对向量,

原理：无符号数编码的唯一性，函数是一个双射。

最大值,最小值0

 

补码编码：

补码编码的定义，对向量：

w位补码所能表示的值的范围，能表示的最小值是位向量[10...0]，整数值为。最大值是[01...1],整数值是。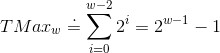

原理：补码编码的唯一性。

 

使用宏能保证：不论代码是如何被编译的，都能生成正确的格式字符串。

有符号数还有两种标准的表示方法：

反码：除了最高有效位的权是,而不是,它和补码是一样的：.

原码：最高有效位是符号位，用来确定剩下的位应该取负权还是正权：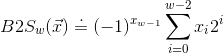

 

有符号数和无符号数之间的转换：

对于大多数C语言的实现，处理同样字长的有符号数和无符号数之间相互转换的一般规则是：数值可能会改变，但是位模式不变。强制类型转换的结果保持位值不变，只是改变了解释这些位的方式。

给定位模式的补码和无符号数之间的关系可以表示成T2U函数的一个属性：

原理：补码转换为无符号数，对满足的x有：

无符号数u和有符号数关系，:

原理：无符号数转换为补码，对满足的u有：

无符号数和有符号数的转换，如果在某范围内，数值不变的，或者就是加减了个.

C语言对同时包含有符号和无符号数表达式的处理，会隐式地将有符号参数强制转换为无符号数，并假设这两个数都是非负的。

 

扩展一个数字的位表示：

要将一个无符号数转换为一个更大的数据类型，只要简单的在表示的开头添加0,这种运算称为零扩展。

要将一个补码数字转换为一个更大的数据类型，可以执行符号扩展，在表示中添加最高有效位的值。(推导就没看了）

 

截断数字：

截断无符号数：令，而是将其截断为k位的结果，等于，令,则.

 

整数运算：

为参数x,y定义一个运算：,其中.该操作是，把整数和x+y截断为w位得到的结果，再把这个结果看作是一个无符号数。

原理：无符号数加法

对满足的x和y有：

 

原理：检测无符号数加法中的溢出。对在范围中的x和y,令,则当且仅当s

原理：无符号数求反。对满足的任意x，其w位的无符号逆元由下式给出：.

 

补码加法：

定义为整数和x+y被截断为w位的结果，并将这个结果看作是补码数。

原理：补码加法。对满足的整数x和y，有：

原理：检测补码加法中的溢出。对满足的x和y，令。当且仅当x>0,y>0，但时，计算s发生了正溢出。当且仅当x<0,y<0,但时，计算s发生了负溢出。

 

补码的非：

对满足的x，其补码的非由下式给出，

补码非的位级表示：

执行位级补码非的第一种方法：对每一位求补，再对结果加1。对x计算结果，-x 和~x+1的结果一样。

第二种方法是，只要x不等于0，存在从右往左的第一位1，这一位作为边界，然后它左边的所有位取反。

 

无符号乘法：

C语言中的无符号乘法被定义为产生w位的值，就是2w位的整数乘积的低w位表示的值。将这个值表示为。

原理：无符号数乘法。对满足的x和y有：

 

补码乘法：

C语言中的有符号乘法是通过将2w位的乘积截断为w位来实现的。这个数值表示为,将一个补码截断为w位相当于先计算该值模,再把无符号数转换为补码。

原理：对满足,的x和y有：

 

无符号和补码乘法的位级等价性。

 

乘以常数：

原理：乘以2的幂。设x为位模式表示的无符号整数。对于任何，认为给出了的w+k位的无符号表示，右边增加了k个0.

整数乘法比移位和加法的代价大很多，许多C编译器试图用移位、加法和减法的组合来消除很多整数乘以常数的情况。

比如，一个数，把他写成几个2的某某次方的求和，然后使用移位就可以。

 

除以2的幂：

原理：除以2的幂的无符号除法。C变量X和K有无符号数值x,k，且,则C表达式产生数值

 

原理：除以2的幂的补码除法，向上舍入。C变量X和K分别有补码值x和无符号数值k，且,则当执行算术移位时，C表达式产生数值

在这里，移位前先加了个“偏置”，为了修正不合适的舍入。

 

浮点数：

IEEE浮点表示：

IEEE浮点标准用的形式表示一个数

这部分有点难，懂了一些，笔记就不记了，有点多。

舍入：IEEE浮点格式定义了四种不同的舍入方式。默认的是找到最接近的匹配，其他三种用于计算上界和下界。

向偶数舍入也被称为向最接近的值舍入。

 

浮点加法和浮点乘法不具有结合性，浮点乘法在加法上不具备分配性。